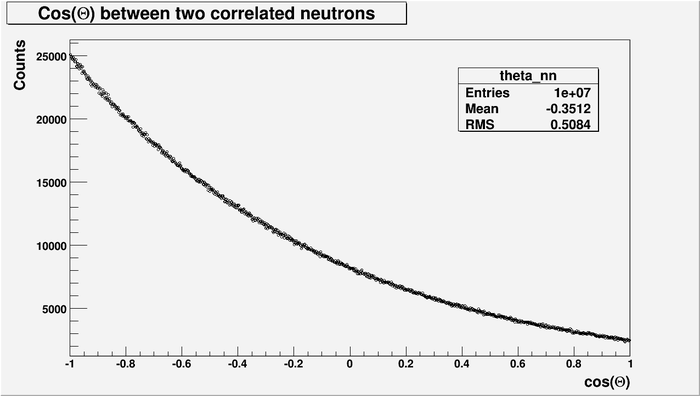
Cos(Theta) between two correlated neutrons. Unpolarized case.
Jump to navigation
Jump to search
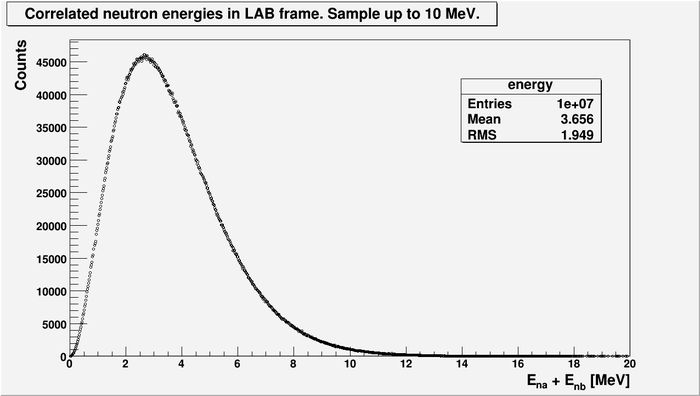
Follow are some Monte Carlo simulations of 2n correlations. One neutron are from one FF, two neutrons per fission. No accidental neutron was considered, all neutrons are correlated. Total 10M events was simulated. Every neutron was sampled up to 10 MeV. The polarization of gammas are zero.
Even for the case above (without energy cut) the asymmetry between neutrons emitted anti-parallel and parallel is large and about 9.
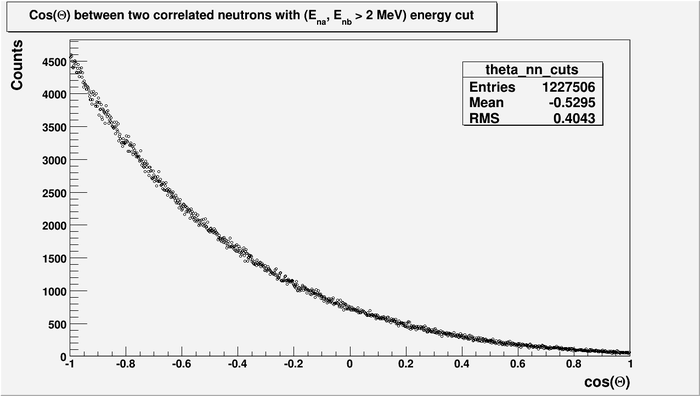
But let's do the energy cut.
The calculated asymmetry from the last plot is:
here:
- are all events with angle between two neutrons is
- are all events with angle between two neutrons is
The yields are:
Looks good, but we need big statistics. We can increase statistics by decreasing the energy cut but we will reduce the asymmetry.