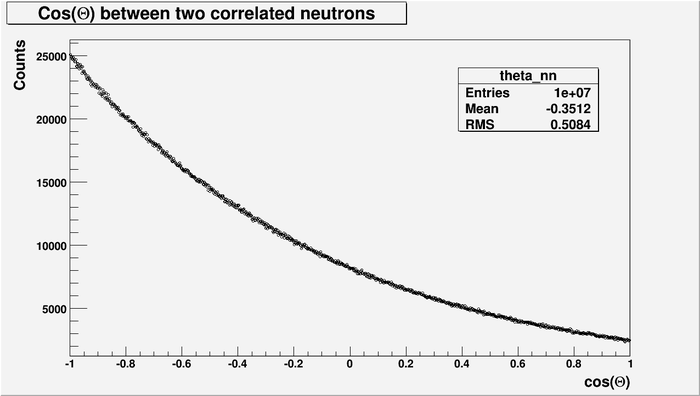
Cos(Theta) between two correlated neutrons. Unpolarized case.

go back

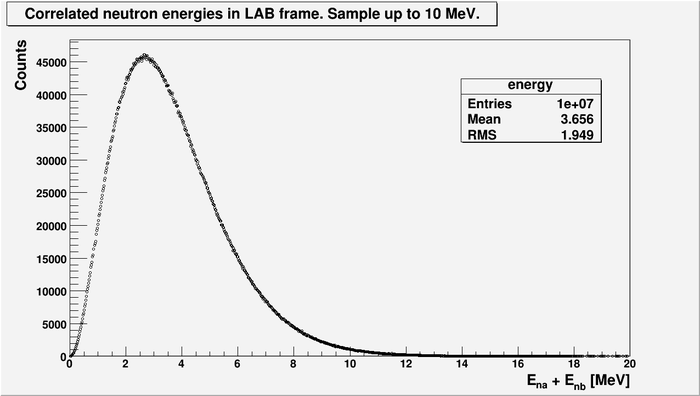
Follow are some Monte Carlo simulations of 2n correlations. One neutron are from one FF, two neutrons per fission. No accidental neutron was considered. Total 10M events was simulated. The polarization of gammas are zero.

Below is the energy spectrum of two correlated neutrons in LAB frame. Sampled up to 10 MeV.

Below is [math]cos(\Theta)[/math] between two correlated neutrons. Integrated over all energy spectrum without any energy cut.

Even for the case above (without energy cut) the asymmetry between neutrons emitted anti-parallel and parallel is large and about 9.

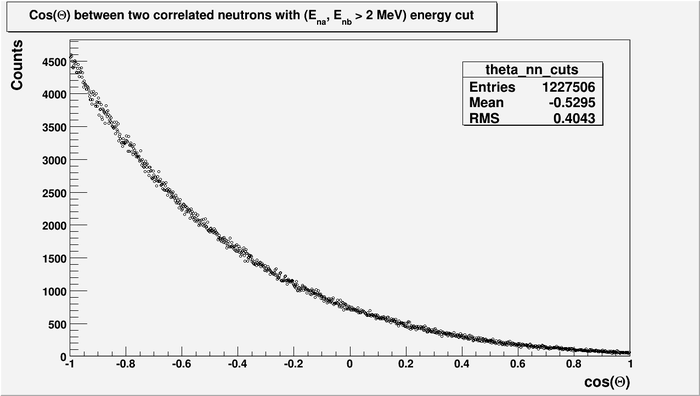
But let's do the energy cut.

The calculated asymmetry from the last plot is:

[math]\mbox{Asymmetry} = \frac{\mbox{counts}\ \leftrightarrows}{\mbox{counts}\ \leftleftarrows} = \frac{209,578}{3,219} = 65.10655[/math]

here:

• [math]\mbox{counts}\ \leftrightarrows[/math] are all events with angle between two neutrons is [math]\Theta \approx (180\pm25)^o[/math]
• [math]\mbox{counts}\ \leftleftarrows[/math] are all events with angle between two neutrons is [math]\Theta \approx (0\pm25)^o[/math]

That angles correspond to 90 cm long detector located about 2 m away from target. That is good for time of flight technique.

The yields are:

[math]\mbox{Energy}\ \mbox{Cut}\ \mbox{Yield} = \frac{\mbox{counts}\ \mbox{with}\ \mbox{cut}}{\mbox{total}\ \mbox{counts}} = \frac{1,227,505}{10,000,000} = 0.12277[/math]

[math]\mbox{Asymmetry}\ \mbox{Yield} = \frac{(\mbox{counts}\ \leftrightarrows) + (\mbox{counts}\ \leftleftarrows)}{\mbox{total}\ \mbox{counts}} = \frac{209,578 + 3,219}{10,000,000} = 0.02128[/math]

Looks good, but we need big statistics. We can increase statistics by decreasing the energy cut but we will reduce the asymmetry.