Cos(Theta) between two correlated neutrons. Unpolarized case.

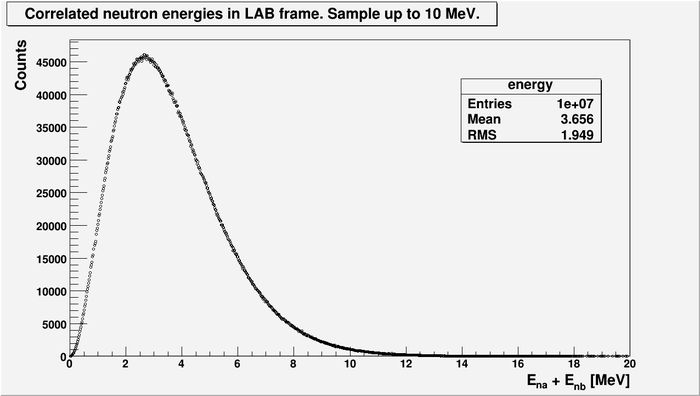
Below is the energy spectrum of two correlated neutrons in LAB frame.

• 10 million events total
• Sampled up to 10 MeV.

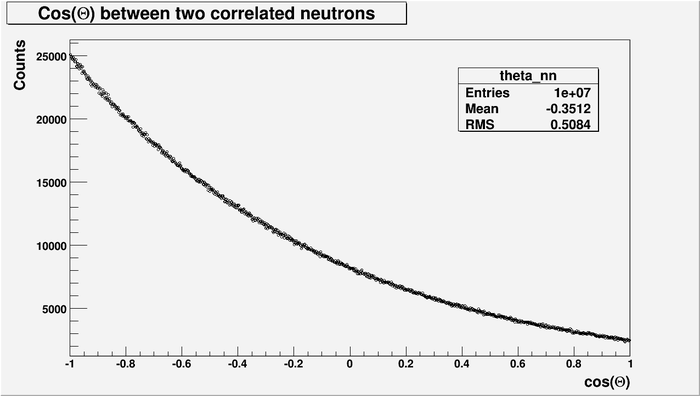
Below is [math]cos(\Theta)[/math] between two correlated neutrons.

• Integrated over all energy spectrum.
• No energy cut was made.

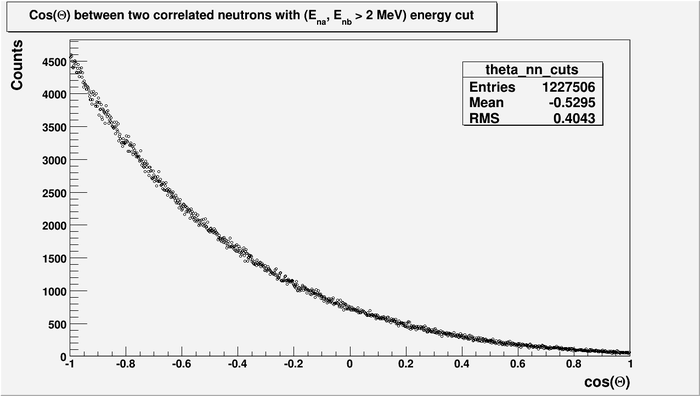
And with energy cut.

The calculated asymmetry from the last plot is:

[math]\mbox{Asymmetry} = \frac{\mbox{counts}\ \leftrightarrows}{\mbox{counts}\ \leftleftarrows} = \frac{209,578}{3,219} = 65.10655[/math]

here:

• [math]\mbox{counts}\ \leftrightarrows[/math] are all events with angle between two neutrons is [math]\Theta \approx (180\pm25)^o[/math]
• [math]\mbox{counts}\ \leftleftarrows[/math] are all events with angle between two neutrons is [math]\Theta \approx (0\pm25)^o[/math]

that corresponds the 90 cm long detector located about 2 m away from target that is pretty good for time of flight technique.

Also my Yields are:

[math]\mbox{Energy}\ \mbox{Cut}\ \mbox{Yield} = \frac{\mbox{counts}\ \mbox{with}\ \mbox{cut}}{\mbox{total}\ \mbox{counts}} = \frac{1,227,505}{10,000,000} = 0.12277[/math]

[math]\mbox{Asymmetry}\ \mbox{Yield} = \frac{(\mbox{counts}\ \leftrightarrows) + (\mbox{counts}\ \leftleftarrows)}{\mbox{total}\ \mbox{counts}} = \frac{209,578 + 3,219}{10,000,000} = 0.02128[/math]

Looks good, but we need big statistics!