Cos(Theta) between two correlated neutrons. Unpolarized case.

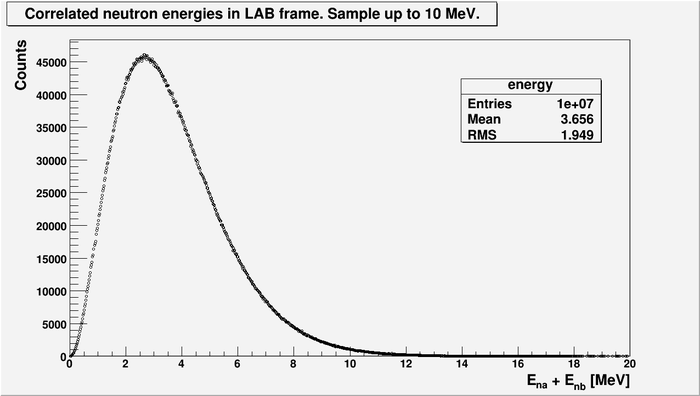
Below is the energy spectrum of two correlated neutrons in LAB frame. 10 million events. Sampled up to 10 MeV.

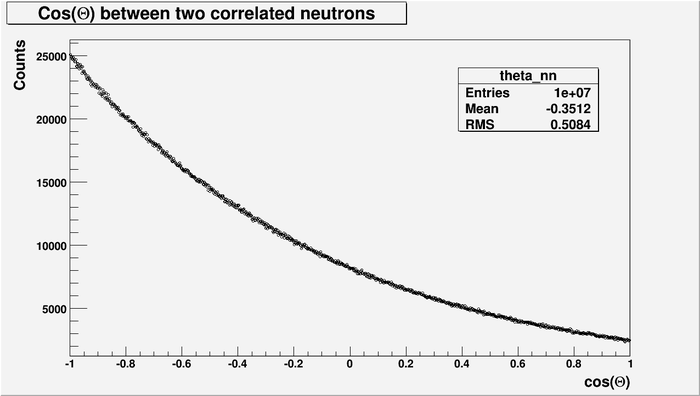
Below is [math]cos(\Theta)[/math] between two correlated neutron. No energy cut was made. Integrated over all energy spectrum.

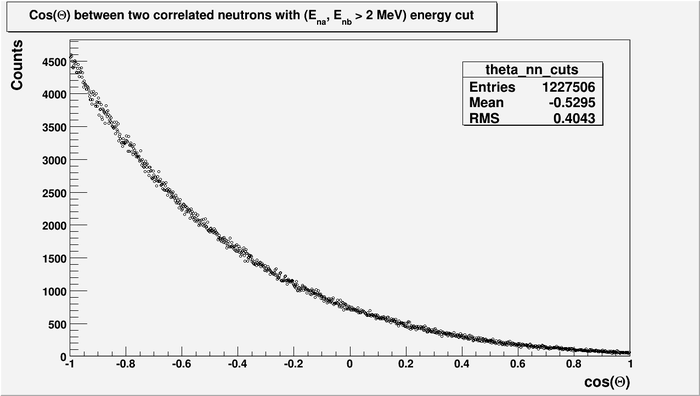
And with energy cut.

The calculated asymmetry between neutron emitted in one direction and in opposite directions is:

[math]Asymmetry = \frac{counts anti-parallel}{counts\ parallel} = frac{209,578}{3,219} = 65.11[/math]

here:

• count anti-parallel are all events with angle between two neutron is [math]cos(\Theta_{nn}) \lt -0.9[/math] that is large enough angle [math]\Theta = (180\pm25)^o\lt math\gt *count parallel are all events with angle between two neutron is \lt math\gt cos(\Theta_{nn}) \gt 0.9[/math] that is large enough angle [math]\Theta = (0\pm25)^o\lt math\gt :\lt math\gt Energy\ Cut\ Yield \frac{counts\ with\ cut}{counts\ without\ cut} = \frac{1,227,505}{10,000,000} = 0.12277[/math]

[math]Asymmetry\ Yield \frac{(counts\ anti-parallel) + (counts\ particle)}{event\ without\ cut} = \frac{209,578 + 3,219}{10,000,000} = 0.02128[/math]

Looks good, but we need big statistics!