Tamar Electron and Pion Efficiency
Particle ID
The correct identification of an electron and a pion is the main requirement for a semi-inclusive analysis. unfortunately, the pion is able to generate cerenkov radiation an as a result be misidentified as an electron. This contamination of the electron sample is removed using the cuts on the energy deposited in the electromagnetic calorimeter, the number of photoelectrons in the Cherenkov counter and fiducial cuts on the detector acceptance.
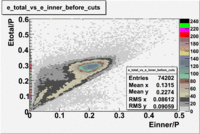
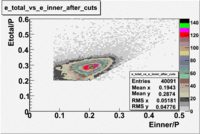
The energy deposition in the calorimeter for electrons and pions is different. Pions are minimum ionizing charge particles depositing into the calorimeter which is independent of the pion's momentum once the momentum is above ~ 0.08 GeV. On the other hand, electrons produce photoelectrons and create electromagnetic shower releasing the energy into the calorimeter which is proportional to their momentum. In order to remove contamination due to the energy deposition in the calorimeter the following cut was introduced: . The cut was also applied to the energy collected in the inner part of the calorimeter: , because the ratio of the energy deposited in the total to the inner calorimeter depends on the thickness of the detector and is a constant.
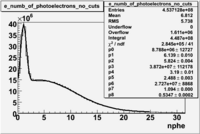
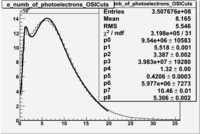
In addition to the cut on the energy deposited into the electromagnetic calorimeter, the misidentified electrons were excluded requiring a signal in the threshold CLAS Cherenkov detector. Pion's misidentified as electrons have been shown to produce around ~1.5 photoelectons in the cherenkov detector, as shown below. Geometrical cuts on the location of the particle at the entrance to the cerenkov detector were applied to reduce the pion contamination. The second histogram below shows that after cuts the peak around 1.5 is substantially reduced.
| No cuts | OSI Cuts |
Inclusive Efficiency
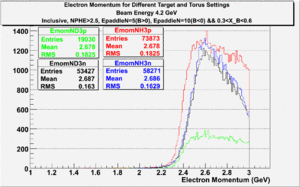
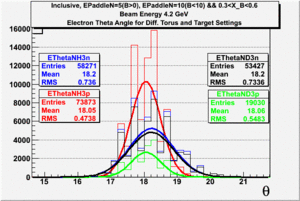
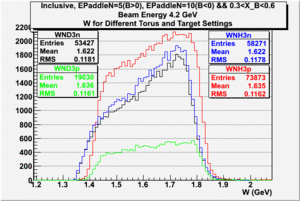
In this chapter we describe the electron paddle number selection and electron efficiency. The analysis were performed on 4.2 GeV data for ND3 and NH3 targets. In the final state, only electron detection was required(inclusive case). The histograms on Fig. 2.1 represent the scattered electron paddle number for both types of target. The electron paddle number 10 and 5 were chosen for B<0 and B>0 respectively. The kinematics(Momentum, scattering angle and invariant mass) for selected electron paddle numbers are shown on Fig. 2.2.
| Target Type, Polarity, Beam Energy | Electron Paddle Number |
| ND3, B<0, 4.2 GeV | 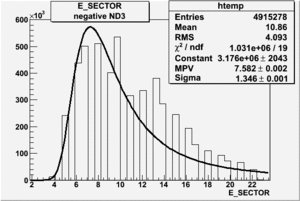
|
| ND3, B>0, 4.2 GeV | 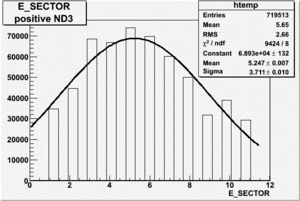
|
| NH3, B<0, 4.2 GeV | 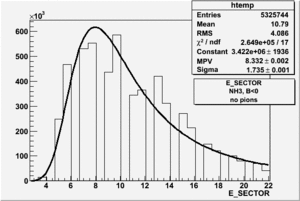
|
| NH3, B>0, 4.2 GeV | 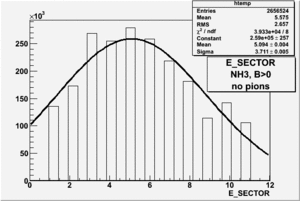
|
Figure 2.1. Electron Paddle Number for NH3 and ND3 targets.
 |
 |
|
| Electron Momentum((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) | Electron Scattering Angle ((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) | W Invariant mass((NH3,B>0), (NH3,B<0), (ND3,B>0) && (ND3,B<0)) |
Figure 2.1. Electron Kinematics.