Lab 17 RS
The JFET (Junction Field Effect Transistor n-channel)
File:JFET MPF102 DataSheet.pdf
1). Complete the table below for the JFET.
| Characteristic | Symbol | Min | Max | Unit |
| Zero-Gate-Voltage Drain Current | 2.0 | 20 | mAdc | |
| Gate-Source Cutoff Voltage | - | -8.0 | Vdc | |
| 3.3 M | ||||
| 1.0 M | ||||
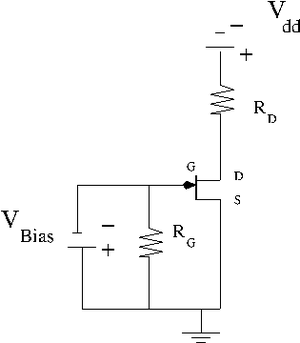
2.) Construct the JFET circuit below.
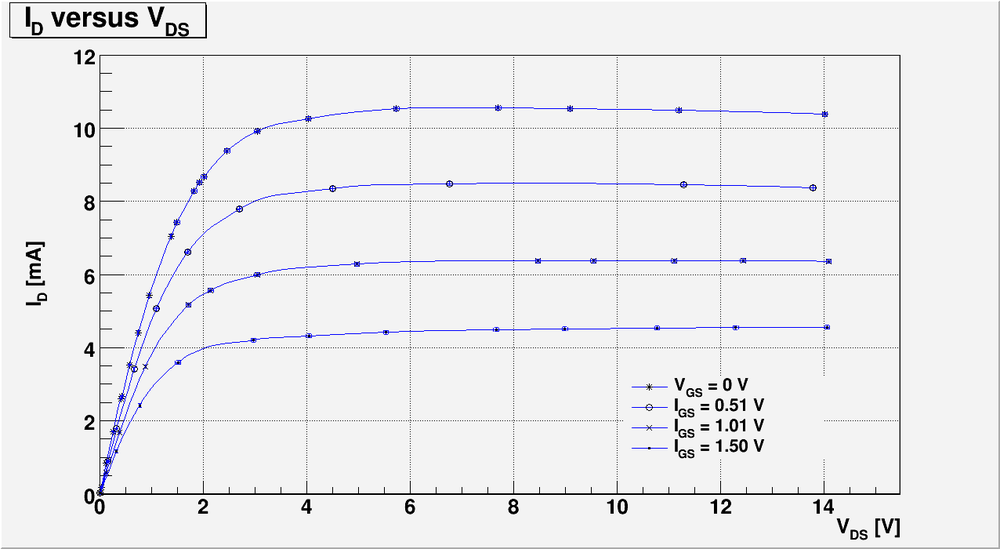
3.) Plot measurements of -vs- by varying for = 0, 0.5, 1.0, 1.5 V. (40 pnts)
I have used the following resistors:
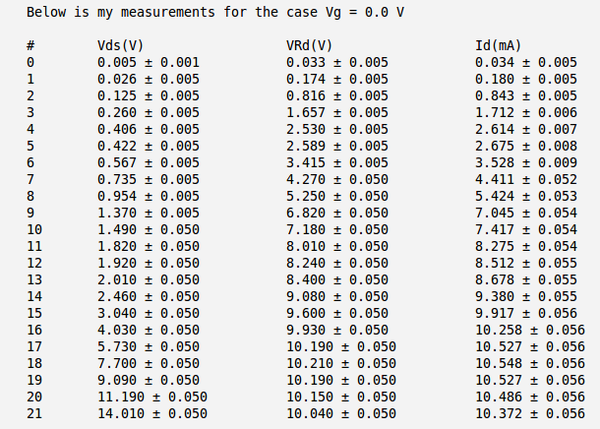
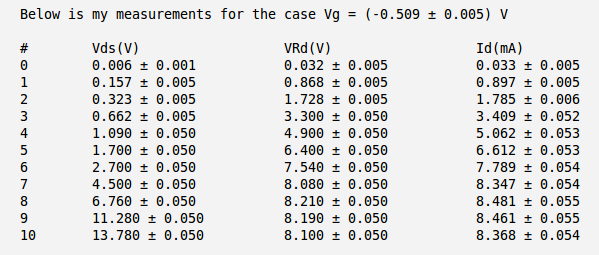
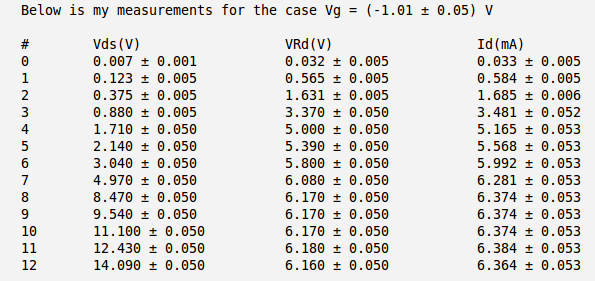
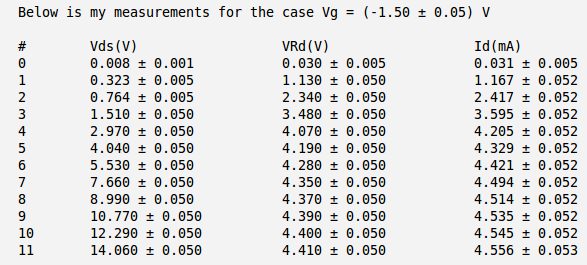
Below is the table with my measurements of voltages and and calculation of the current . Here I have used the meter to measure directly the voltage drop between the drain and source and to measure the voltage drop on resistor .
So my calculated current becomes:
.
And below I have plotted four curves as function of for four different values of
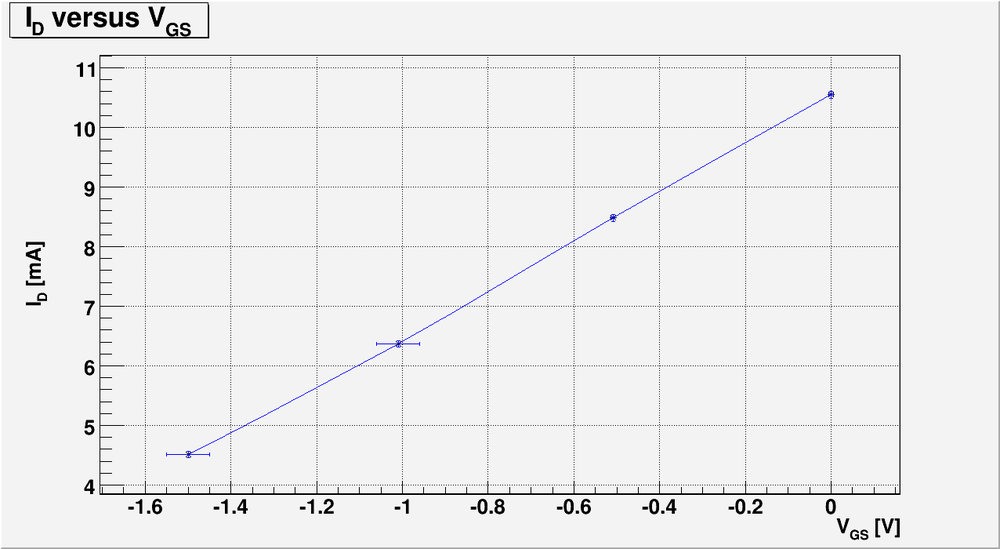
4.) Plot -vs- (30 pnts)
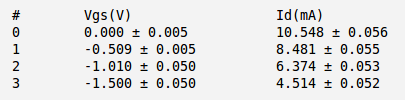
For every measured values I have picked up the current values in the middle of saturation region of each line as follow:
And below is my plot of -vs- :
5.) Calculate for your JFET (20 pnts)
For common source configuration JFET:
So to calculate math>y_{fs}</math> we need to know function . Lets approximate this function by line:
Question
Does depend on? (10 pnts)
Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement