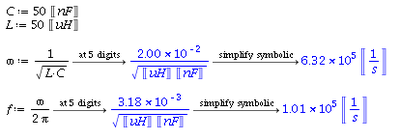Lab 5 RS

Go Back to All Lab Reports

LC Resonance circuits

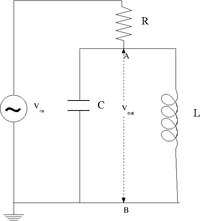
The LC cicuit

1. Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use [math]L[/math] = 10 - 100 [math]\mu H[/math], R = 1k

[math]\Omega[/math] .

[math]\omega_0=\frac{1}{\sqrt{\mbox{LC}}}[/math]

I choose the following values for [math]\mbox{R}[/math] and [math]\mbox{C}[/math]:

[math]R=aaa\ \Omega[/math]

[math]C=bbb\ \mu F[/math]

So the resonance frequency is [math]\omega_0=\frac{1}{\sqrt{aaa\ \Omega\ bbb\ \mu F }} = ccc\ \frac{\mbox{rad}}{\mbox{sec}}[/math]

Or [math]f=\frac{\omega_0}{2\pi} = ddd\ \mbox{kHz}[/math]

Let's estimate:

1. Construct the LC circuit using a non-polar capacitor
2. Measure the Gain [math]\equiv \frac{V_{out}}{V_{in}}[/math] as a function of frequency. (25 pnts)
3. Compare the measured and theoretical values of the resonance frequency ([math]\omega_{L}[/math]) (10 pnts)

Questions

1. Is there a value of [math]R[/math] in which [math]V_{out} \approx V_{in}[/math] at resonance. What is the value?(5 pnts)

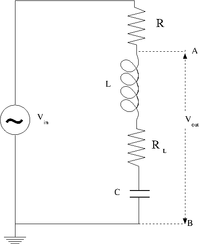
The RLC cicuit

1. Design and construct a series LRC circuit.
2. Measure and Graph the Gain as a function of the oscillating input voltage frequency. (25 pnts)
3. Measure and Graph the Phase Shift as a function of the oscillating input voltage frequency. (25 pnts)

Questions

1. What is the current [math]I[/math] at resonance? (5 pnts)
2. What is the current as [math]\nu \rightarrow \infty[/math]? (5 pnts)

LC Resonance circuits

The LC cicuit

Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use [math]L[/math] = 10 - 100 [math]\mu H[/math].

[math]\omega_0=\frac{1}{\sqrt{\mbox{LC}}}[/math]

I choose the following values for [math]\mbox{R}[/math] and [math]\mbox{C}[/math]:

[math]R=aaa\ \Omega[/math]

[math]C=bbb\ \mu F[/math]

So the resonance frequency is [math]\omega_0=\frac{1}{\sqrt{aaa\ \Omega\ bbb\ \mu F }} = ccc\ \frac{\mbox{rad}}{\mbox{sec}}[/math]

Or [math]f=\frac{\omega_0}{2\pi} = ddd\ \mbox{kHz}[/math]

Let's estimate:

Questions

1. If r=0, show that [math]Q = \frac{1}{\omega_0 R_L C}[/math]. (10 pnts)
2. Show that at resonance[math] Z_{AB} \approx Q \omega_0 L[/math]. (10 pnts)

The LRC cicuit

1. Design and construct a series LRC circuit.
2. Measure and Graph the Gain as a function of the oscillating input voltage frequency. (20 pnts)

Questions

1. What is the current [math]I[/math] at resonance? (5 pnts)
2. What is the current as [math]\nu \rightarrow \infty[/math]? (5 pnts)

Forest_Electronic_Instrumentation_and_Measurement

Go Back to All Lab Reports