RLC circuit
An RLC circuit is a Resistor, an Inductors, and a Capacitor in series with an electromotive force.
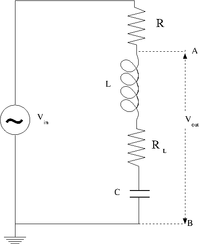
Effective impedance
- [math]X_{out} = R_L + X_C + X_L = R_L + \frac{1}{i \omega C} + i \omega L[/math]
- [math]\left | X_{out} \right | = \sqrt{\left [ R_L + i \left (\frac{-1}{\omega C} + \omega L\right ) \right ]\left [ R - i \left (\frac{-1}{\omega C} + \omega L\right ) \right ]^*}[/math]
- [math]= \sqrt{ R_L^2 + \left ( \omega L - \frac{1}{\omega C} \right )^2}[/math]
Gain
Loop Theorem
- [math]V_{in} = I (R+ X_{out})[/math]
Voltage Divider
- [math]V_{AB}=V_{out} = \frac{X_{out}}{R + X_{out}}V_{in}[/math]
- [math]\left | \frac{V_{out}}{V_{in}}\right | = \sqrt{\left [ \frac{X_{out}}{R + X_{out}}\right ]\left [ \frac{X_{out}}{R + X_{out}}\right ]^*}[/math]
[math]R_L + i \left ( \omega L - \frac{1}{\omega C}\right)[/math]
- [math]\left | \frac{V_{out}}{V_{in}}\right | = \sqrt{\left [ \frac{R_L + i \left ( \omega L - \frac{1}{\omega C}\right)}{R + R_L + i \left ( \omega L - \frac{1}{\omega C}\right)}\right ]\left [ \frac{R_L + i \left ( \omega L - \frac{1}{\omega C}\right)}{R + R_L + i \left ( \omega L - \frac{1}{\omega C}\right)}\right ]^*}[/math]
- [math] = \sqrt{\frac{R_L^2 + \left ( \omega L - \frac{1}{\omega C}\right)^2}{(R + R_L)^2 + \left ( \omega L - \frac{1}{\omega C}\right)^2}}[/math]
- [math] = \sqrt{\frac{R_L^2 + \left ( \frac{\omega^2 LC - 1}{\omega C}\right)^2}{(R + R_L)^2 + \left ( \frac{\omega^2 LC - 1}{\omega C}\right)^2}}[/math]
Let
- [math]\omega_0 = \sqrt{\frac{1}{LC}}[/math]
Then
- [math]\left | \frac{V_{out}}{V_{in}}\right | = \sqrt{\frac{R_L^2 + \left ( \frac{\omega^2 LC - 1}{\omega C}\right)^2}{(R + R_L)^2 + \left ( \frac{\omega^2 LC - 1}{\omega C}\right)^2}}[/math]
Phase shift