Go Back
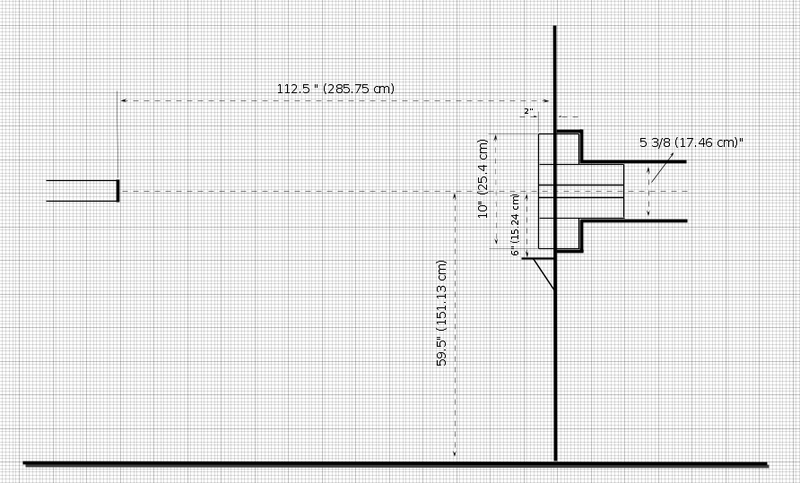
90[math]^o[/math] exit port measurements
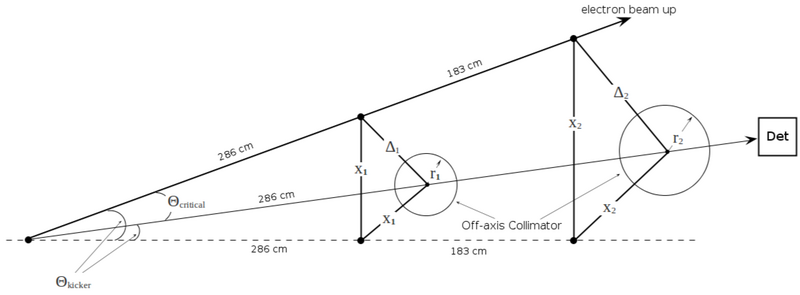
Critical and Kicker angles
[math]\Theta_C = \frac{m_ec^2}{E}[/math]
[math]\Theta_K = tan^{-1}\left(\frac{x_1}{286}\right)
= tan^{-1}\left(\frac{1}{\sqrt{2}}\ \frac{\Delta_1}{286}\right)
= tan^{-1}\left(\frac{1}{\sqrt{2}}\ tan(\Theta_C)\right)[/math]
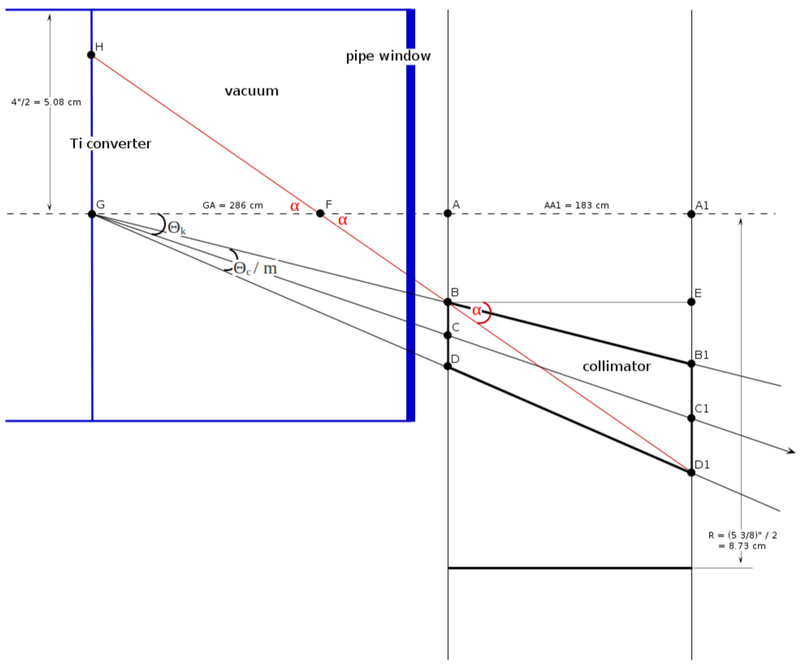
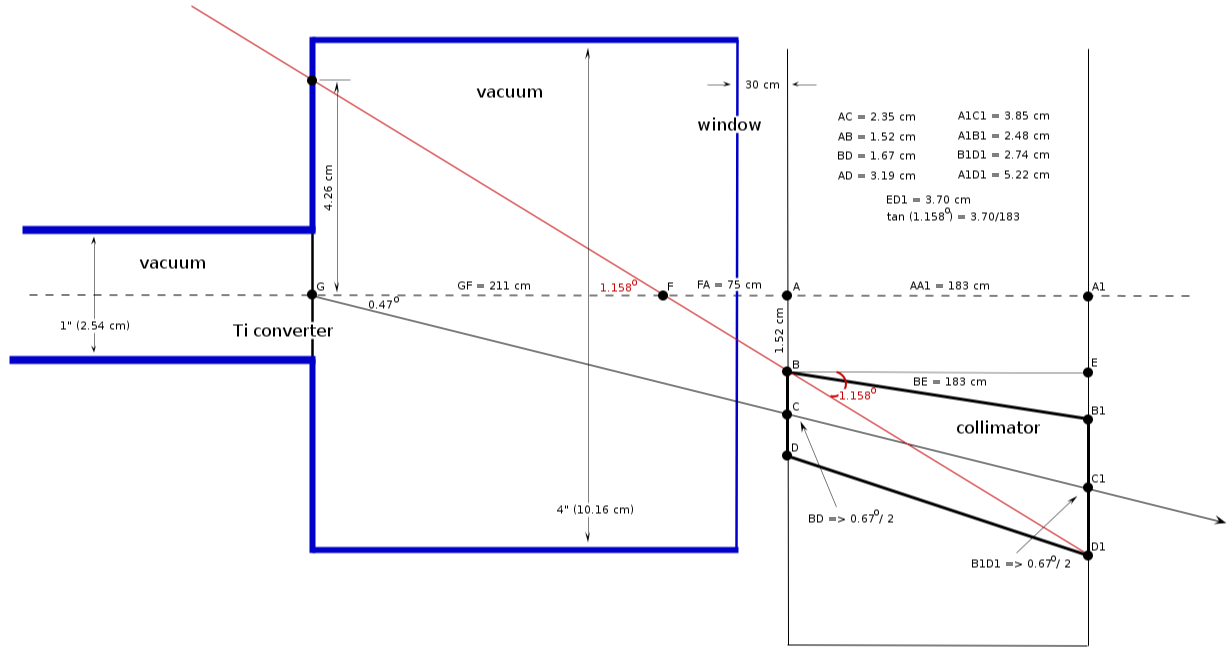
Geometry calculation
| beam energy
|
[math]\Theta_C / m[/math]
|
[math]\Theta_C[/math]
|
[math]\Theta_K[/math]
|
[math]\alpha[/math]
|
[math]AC[/math]
|
[math]A_1C_1[/math]
|
[math]BD[/math]
|
[math]B_1D_1[/math]
|
[math]A_1D_1[/math]
|
[math]FA[/math]
|
[math]GH[/math]
|
| 25 MeV |
[math]\Theta_C / 2[/math] |
[math]1.17^o[/math] |
[math]0.83^o[/math] |
[math]2.03^o[/math]
|
4.13 cm |
6.78 cm |
2.92 cm |
4.79 cm |
9.18 cm > 8.73 cm |
75 cm |
7.49 cm > 5.08 cm
|
| 25 MeV |
[math]\Theta_C / 3[/math] |
[math]1.17^o[/math] |
[math]0.83^o[/math] |
[math]1.63^o[/math]
|
4.13 cm |
6.78 cm |
1.95 cm |
3.20 cm |
8.37 cm < 8.73 cm |
111 cm |
4.99 cm < 5.08 cm
|
| 25 MeV |
[math]\Theta_C / 4[/math] |
[math]1.17^o[/math] |
[math]0.83^o[/math] |
[math]1.43^o[/math]
|
4.13 cm |
6.78 cm |
1.46 cm |
2.40 cm |
7.98 cm < 8.73 cm |
136 cm |
3.74 cm < 5.08 cm
|
| 44 MeV |
[math]\Theta_C / 2[/math] |
[math]0.67^o[/math] |
[math]0.47^o[/math] |
[math]1.16^o[/math]
|
2.35 cm |
3.85 cm |
1.66 cm |
2.72 cm |
5.21 cm < 8.73 cm |
75 cm |
4.26 cm < 5.08 cm
|
| 44 MeV |
[math]\Theta_C / 3[/math] |
[math]0.67^o[/math] |
[math]0.47^o[/math] |
[math]0.93^o[/math]
|
2.35 cm |
3.85 cm |
1.11 cm |
1.82 cm |
4.76 cm < 8.73 cm |
111 cm |
2.84 cm < 5.08 cm
|
| 44 MeV |
[math]\Theta_C / 4[/math] |
[math]0.67^o[/math] |
[math]0.47^o[/math] |
[math]0.81^o[/math]
|
2.35 cm |
3.85 cm |
0.83 cm |
1.36 cm |
4.53 cm < 8.73 cm |
136 cm |
2.13 cm < 5.08 cm
|
25 MeV geometry
[math] \Theta_c/4[/math], pipe 3"
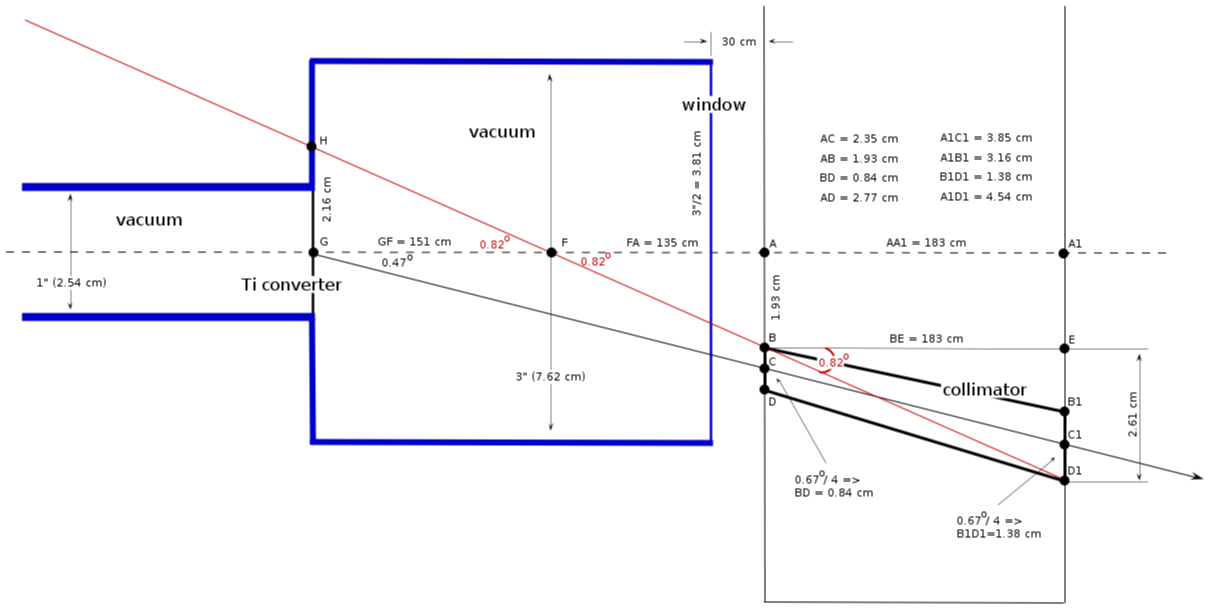
[math] \Theta_c/2[/math], box 3"x4" and then pipe 4"
need to adjust to converter position
Go Back




