Go Back
Minimum accelerator energy to run experiment
condition 1: fitting the collimator size into the hole
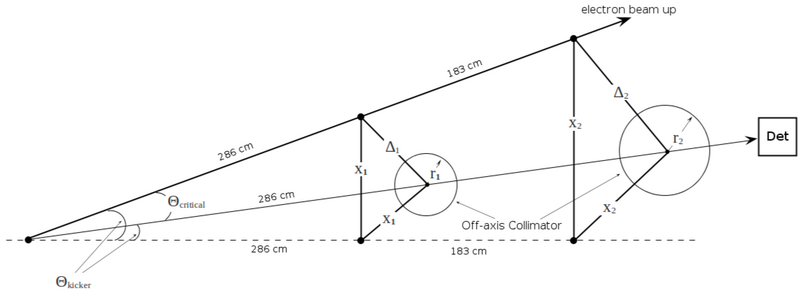
The minimum energy of accelerator (MeV) is limited by fitting the collimator size [math]r_2[/math] into the hole R = 8.73 cm:
[math]x_2 + r_2 = R[/math]
1) Assuming the collimator diameter is [math]\Theta_C[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV [/math]
2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV [/math]
3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/2[/math]:
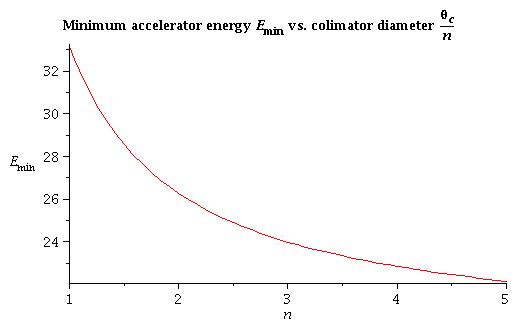
All energy above this line is good to run experiment
condition 2: F1A = 286 cm
1) assuming the collimator diameter is [math]\Theta_C[/math]
[math] E_{min} = 73.7\ MeV [/math]
2) assuming the collimator diameter is [math]\Theta_C/2[/math]
[math] E_{min} = 36.9\ MeV [/math]
3) assuming the collimator diameter is [math]\Theta_C/4[/math]
[math] E_{min} = 18.4\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/m[/math]:
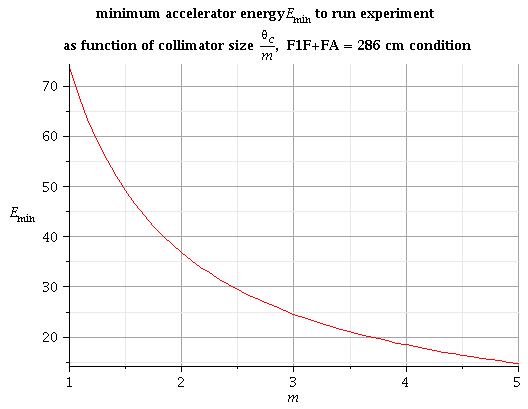
All energy above this line is good to run experiment
both conditions above are together
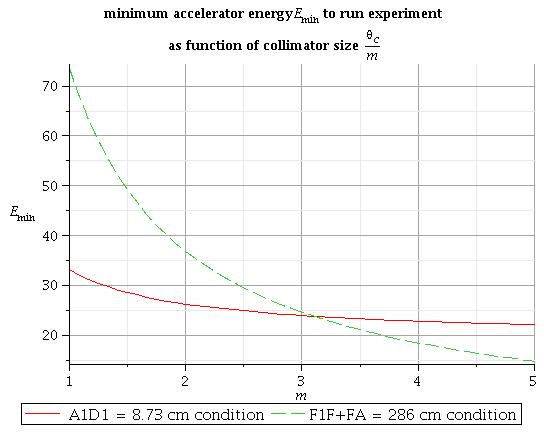
All energy above this lines is good to run experiment
Go Back
Minimum accelerator energy to run experiment
condition 1: fitting the collimator size into the hole

The minimum energy of accelerator (MeV) is limited by fitting the collimator size [math]r_2[/math] into the hole R = 8.73 cm:
[math]x_2 + r_2 = R[/math]
1) Assuming the collimator diameter is [math]\Theta_C[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV [/math]
2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV [/math]
3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/2[/math]:

All energy above this line is good to run experiment
condition 2: F1A = 286 cm
1) assuming the collimator diameter is [math]\Theta_C[/math]
[math] E_{min} = 73.7\ MeV [/math]
2) assuming the collimator diameter is [math]\Theta_C/2[/math]
[math] E_{min} = 36.9\ MeV [/math]
3) assuming the collimator diameter is [math]\Theta_C/4[/math]
[math] E_{min} = 18.4\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/m[/math]:

All energy above this line is good to run experiment
both conditions above are together

All energy above this lines is good to run experiment
Go Back



