Go Back
Minimum accelerator energy to run experiment
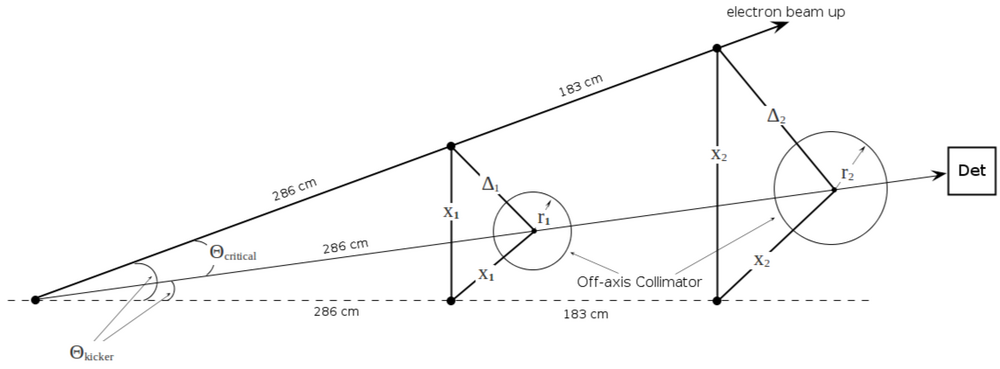
The minimum energy of accelerators defined by fitting collimator size ([math]r_2[/math]) into hole ([math]R_2[/math])
[math]x_2 + r_2 = R[/math]
[math]x = \frac{286}{\sqrt{2}}\ \tan\left(\frac{0.511}{E}\frac{180}{\pi}\right) +
\frac{286}{2}\ \tan\left(\frac{1}{2}\frac{0.511}{E}\frac{180}{\pi}\right) [/math]
25 MeV geometry
critical angle
[math]\Theta_C = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{25\ MeV} = 1.17\ ^o[/math]
kicker angle
[math]\Delta_1 = 286\ cm\ *\ \tan(1.17^o) = 5.84\ cm[/math]
[math]x^2+x^2 = 5.84^2\ cm \ \ \Rightarrow\ \ x = 4.13\ cm[/math]
[math]\Delta_2 = 4.13\ cm \ \ \Rightarrow\ \ \tan^{-1}\left(\frac{4.13}{286}\right) = 0.827\ ^o[/math]
geometry ([math] \Theta_c/2[/math])
collimator center position
[math]286\ cm \cdot \tan (0.827) = 4.13\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (0.827) = 6.77\ cm[/math] (wall 2)
collimator diameter
[math]286\ cm \cdot \tan (1.17/2) = 2.92\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (1.17/2) = 4.79\ cm[/math] (wall 2)
collimator critical angle
[math] AB = AC - BD/2 = (4.13 - 2.92/2)\ cm = 2.67\ cm [/math]
[math] A_1D_1 = A_1C_1 + B_1D_1/2 = (6.77 + 4.79/2)\ cm = 9.165\ cm [/math]
[math]\bigtriangleup BED_1 \Rightarrow \tan (\alpha) = \frac{(9.165 - 2.67)\ cm}{183\ cm} \Rightarrow \alpha = 2.033^o[/math]:
minimal distance from the wall ([math] \Theta_c/2[/math])
[math]\bigtriangleup FAB \Rightarrow FA = \frac{AB}{\tan (2.033^o)} = \frac{2.67\ cm}{\tan (2.033^o)} = 75\ cm [/math]
geometry ([math] \Theta_c/4[/math])
collimator center position
[math]286\ cm \cdot \tan (0.827) = 4.13\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (0.827) = 6.77\ cm[/math] (wall 2)
collimator diameter
[math]286\ cm \cdot \tan (1.17/4) = 1.46\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (1.17/4) = 2.39\ cm[/math] (wall 2)
collimator critical angle
[math] AB = AC - BD/2 = (4.13 - 1.46/2)\ cm = 3.4\ cm [/math]
[math] A_1D_1 = A_1C_1 + B_1D_1/2 = (6.77 + 2.39/2)\ cm = 7.965\ cm [/math]
[math]\bigtriangleup BED_1 \Rightarrow \tan (\alpha) = \frac{(7.965 - 3.4)\ cm}{183\ cm} \Rightarrow \alpha = 1.429^o[/math]:
minimal distance from the wall ([math] \Theta_c/4[/math])
[math]\bigtriangleup FAB \Rightarrow FA = \frac{AB}{\tan (1.429^o)} = \frac{3.4\ cm}{\tan (1.429^o)} = 136\ cm [/math]
Funny pictures...
how it looks 1 ([math] \Theta_c/2[/math], box 3"x4" and then pipe 4")
File:Vacuum pipe collimator .png
how it looks 2 ([math] \Theta_c/4[/math], box 3"x4" and then pipe 4")
File:Vacuum pipe collimator .png
Go Back
