Go Back
90[math]^o[/math] exit port geometry
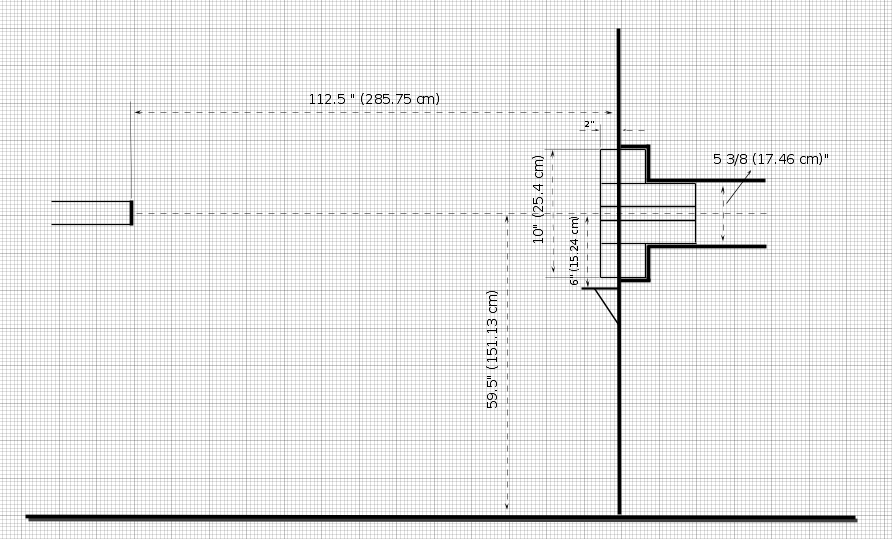
Off-axis collimation geometry
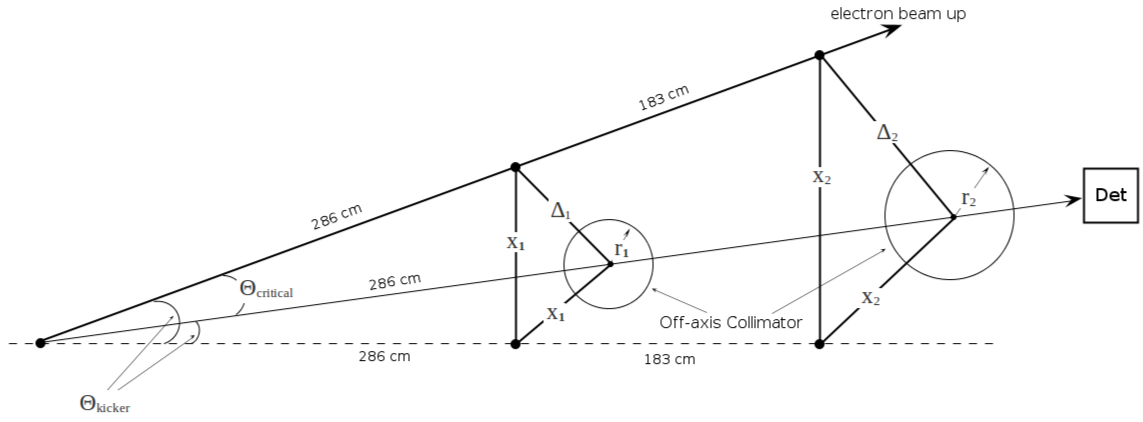
Critical and Kicker angles
[math]\Theta_C = \frac{m_ec^2}{E}[/math]
[math]\Theta_K = tan^-1\left(\frac{x_1}{286}\right)
= tan^-1\left(\frac{1}{\sqrt{2}}\ \frac{\Delta_1}{286}\right)
= tan^-1\left(\frac{1}{\sqrt{2}}\ tan(\Theta_C)\right)[/math]
Collimator location
[math]\Delta_1 = 286\ cm\ \tan(\Theta_C)[/math]
[math]\Delta_2 = (286 + 183)\ cm\ \tan(\Theta_C)[/math]
[math]x_1 = 286\ cm \ \tan(\Theta_K)[/math]
[math]x_1 = (286 +183)\ cm \ \tan(\Theta_K)[/math]
Collimator critical angle
[math]\alpha = [/math]
Vacuum pipe location ([math] \Theta_c/2[/math])
collimator location
1) center position:
[math]286\ cm \cdot \tan (0.47) = 2.35\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (0.47) = 3.85\ cm[/math] (wall 2)
2) collimator diameter:
[math]\Theta_c/2 = 0.67^o/2 = 0.335^o[/math]
[math]286\ cm \cdot \tan (0.335) = 1.67\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (0.335) = 2.74\ cm[/math] (wall 2)
collimator critical angle
[math] AB = AC - BD/2 = (2.35 - 1.67/2)\ cm = 1.52\ cm [/math]
[math] A_1D_1 = A_1C_1 + B_1D_1/2 = (3.85 + 2.74/2)\ cm = 5.22\ cm [/math]
[math] ED_1 = A_1D_1 - A_1E = (5.22 - 1.52)\ cm = 3.70\ cm [/math]
from triangle [math]BED_1[/math]:
[math] \tan (\alpha) = \frac{3.70\ cm}{183\ cm} \Rightarrow \alpha = 1.16^o[/math]
minimal distance from the wall
from triangle FAB:
[math] FA = \frac{AB}{\tan (1.16^o)} = \frac{1.52\ cm}{\tan (1.16^o)} = 75\ cm [/math]
Vacuum pipe location ([math] \Theta_c/4[/math])
collimator location
1) center position:
[math]286\ cm \cdot \tan (0.47) = 2.35\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (0.47) = 3.85\ cm[/math] (wall 2)
2) collimator diameter:
[math]\Theta_c/4 = 0.67^o/4 = 0.168^o[/math]
[math]286\ cm \cdot \tan (0.168) = 0.84\ cm[/math] (wall 1)
[math](286 + 183)\ cm \cdot \tan (0.168) = 1.38\ cm[/math] (wall 2)
collimator critical angle
[math] AB = AC - BD/2 = (2.35 - 0.84/2)\ cm = 1.93\ cm [/math]
[math] A_1D_1 = A_1C_1 + B_1D_1/2 = (3.85 + 1.38/2)\ cm = 4.54\ cm [/math]
[math] ED_1 = A_1D_1 - AB = (4.54 - 1.93)\ cm = 2.61\ cm [/math]
from triangle [math]BED_1[/math]:
[math] \tan (\alpha) = \frac{2.61\ cm}{183\ cm} \Rightarrow \alpha = 0.82^o[/math]
minimal distance from the wall
from triangle FAB:
[math] FA = \frac{AB}{\tan (0.82^o)} = \frac{1.93\ cm}{\tan (0.82^o)} = 135\ cm [/math]
Funny pictures...
how it looks ([math] \Theta_c/2[/math], pipe 3")
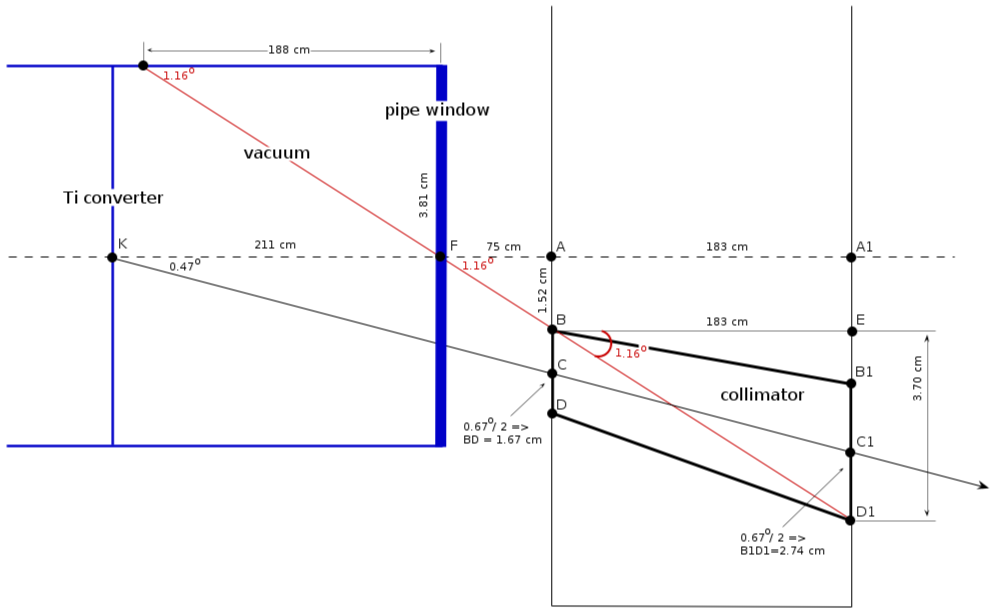
how it looks 1 ([math] \Theta_c/4[/math], pipe 3")
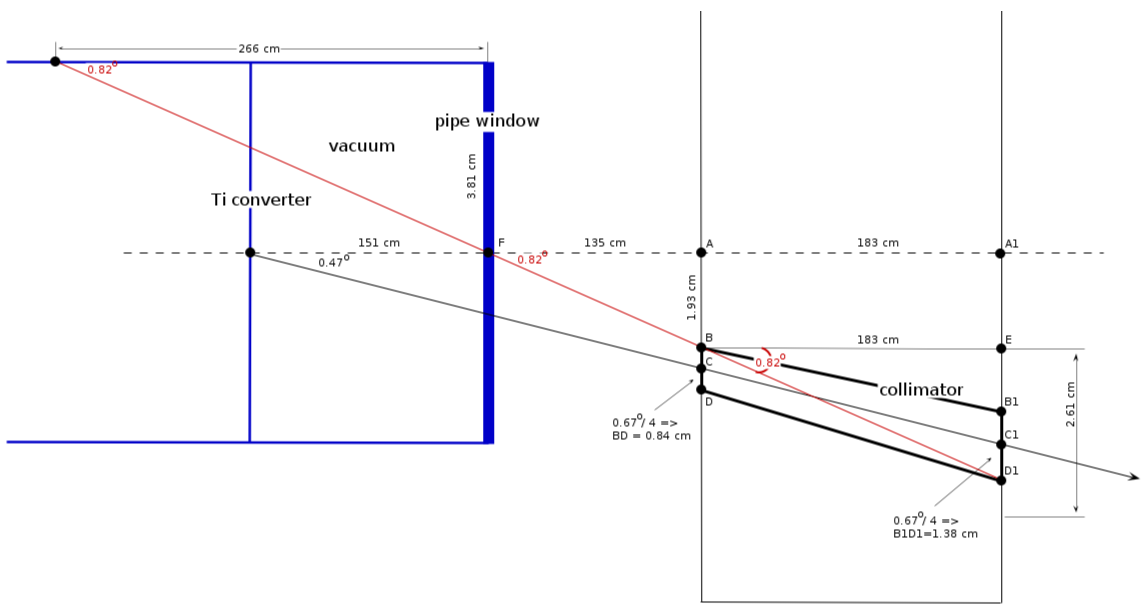
how it looks 2 ([math] \Theta_c/4[/math], pipe 3")
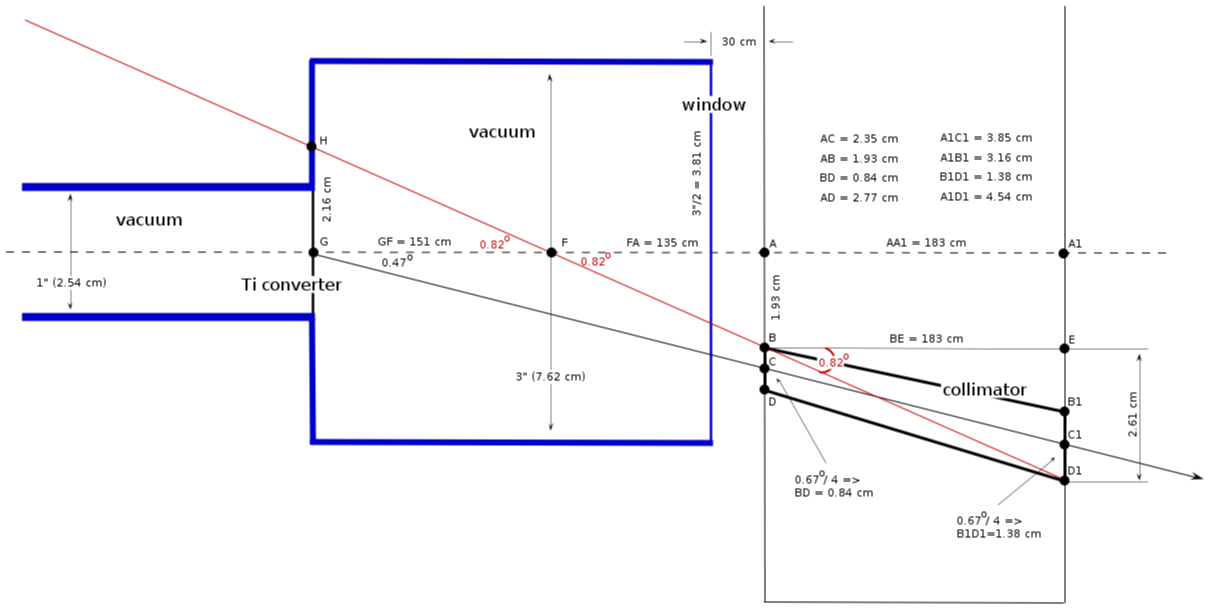
how it looks 4 ([math] \Theta_c/2[/math], pipe (2 1/2)" and then pipe 4")
need to adjust to converter position
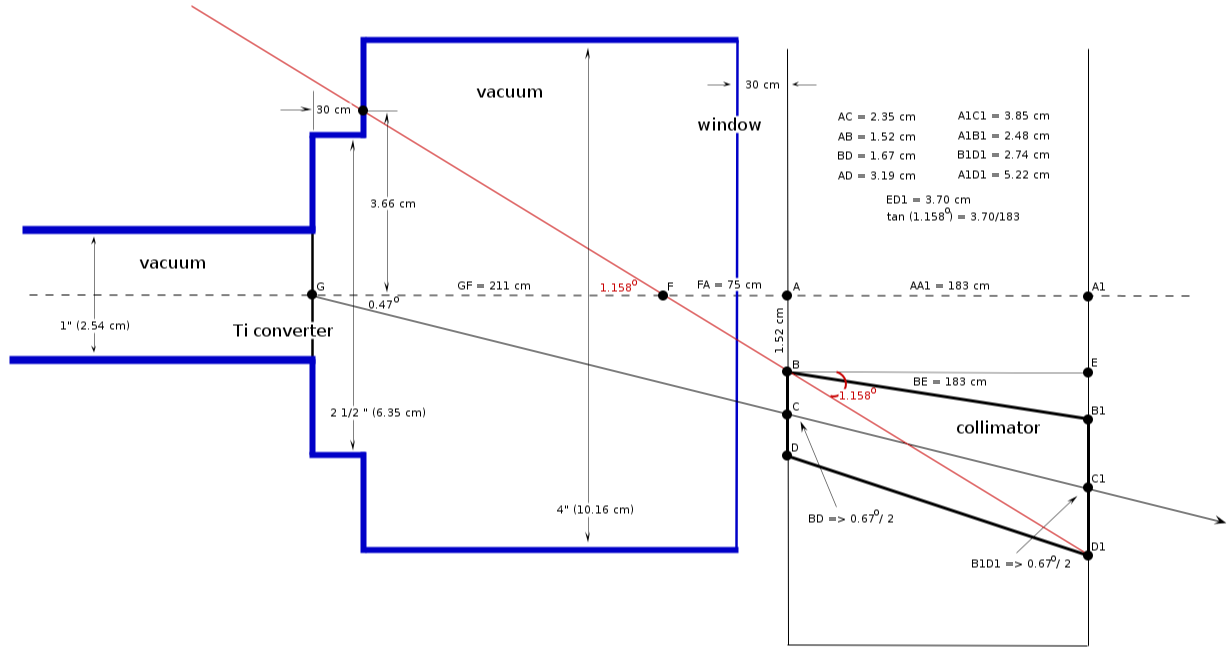
how it looks 5 ([math] \Theta_c/2[/math], box 3"x4" and then pipe 4")
need to adjust to converter position
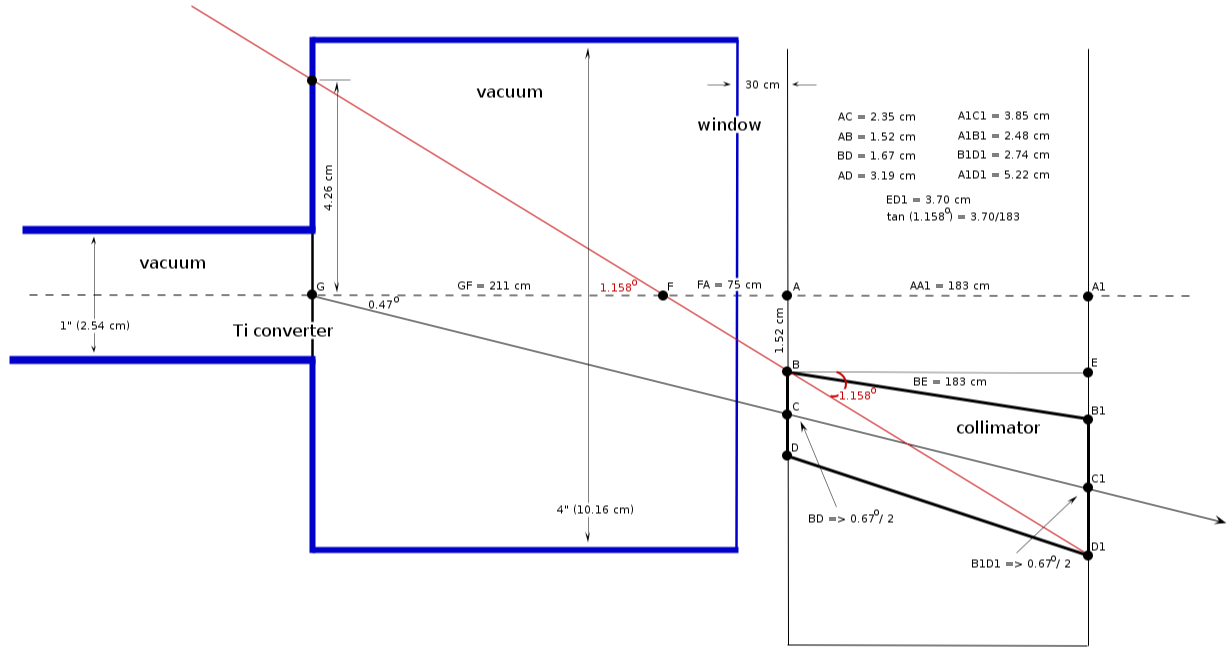
Go Back






