PhD Proposal Tamar

Tamar PhD Proposal

Physics Motivation

Tamuna will have a rough draft of this by Friday July 31,2009. [math]\frac{\Delta d}{d}[/math]

Electron-nucleon semi-inclusive scattering, where the scattered electron and one or more hadrons are detected in coincidence, is a powerful tool for understanding the structure of nucleons.

list out some of the reasons for the above statement and then convert the list into a paragraph

1.) measure polarized structure functions?
2.) test fragmentation?
3.)
4.)

Models provide better understanding of the nucleon structure and "play an important role " in the explanation of the experimental data. Measurement of the double spin asymmetry and the ratio of the polarized valence down quark distribution function to the unpolarized can be used to see the difference between the numerous descriptions of the nucleon structure. pQCD and a hyperfine perturbed constituent quark model predict the scaling variable x_b = 1 corresponds to A_N~1. On the other hand, the well-studied SU(6) constituent quark model for x_b=1 state that A_p=5/9 and A_n=0. The inclusive double spin asymmetry can be written in terms of valence quark distribution functions:

[math]A_{1, p}^{I} = \frac {4\Delta u_v (x) + \Delta d_v (x)} {4 u_v (x) + d_v (x)} [/math] (1)
[math]A_{1, n}^{I} = \frac {\Delta u_v (x) + 4\Delta d_v (x)} {u_v (x) + 4d_v (x)} [/math] (2)

where deltaq_v and q_v are polarized and unpolarized valence quark distribution functions. Quark distribution function q(x) is the probability(density) of finding a quark with fraction x of the proton(neutron) momentum.

The semi-inclusive pion electro-production asymmetries can be written in terms of the valence quark distributions
[math]A_{1, p}[/math]^{[math]\pi^+ - \pi^-[/math]} = [math]\frac {4\Delta u_v (x) - \Delta d_v (x)} {4 u_v (x) - d_v (x)} [/math] (3)

[math]A_{1,2H}[/math]^{[math]\pi^+ - \pi^-[/math]} = [math]\frac {\Delta u_v (x) + \Delta d_v (x)} { u_v (x) + d_v (x)} [/math] (4)

where

[math]A[/math]^{[math]\pi^+ - \pi^-[/math]} =[math]\frac {\sigma^{\pi^+ - \pi^-}_{\uparrow \downarrow} - \sigma^{\pi^+ - \pi^-}_{\uparrow \uparrow}} {\sigma^{\pi^+ - \pi^-}_{\uparrow \downarrow} + \sigma^{\pi^+ - \pi^-}_{\uparrow \uparrow}} [/math] (5)

Experimental Setup

Need an introductory paragrph describing the CLAS detector + target

Target

Target Materials

The EG1 experiment at Jefferson Lab used five different targets to measure polarized structure functions of the nucleon and perform background corrections. The main target materials for the experiment used frozen ammonia, [math]15NH_3[/math], for the polarized protons and deuterated ammonia, [math]15ND_3[/math] for the polarized deuterons. The target vessel, known as the target ladder, was designed and built by collaboration of the Italian Istituto di Fisica Nucleare, TJNAF, Oxford instruments and the University of Virginia. The solid targets(NH3 and ND3) were polarized using the method of Dynamic Nuclear Polarization <ref>Prok Thesis</ref>. Three other targets, C12, liquid He-4 and frozen N15 were used to facilitate the removal of the Nitrogen background resulting from using NH3 and ND3.

there is a figure of merit which considers max polarization and radiation damage, Li-6 is a competitor

Ammonia targets were selected because of their ability to produce high polarization and they are less effected by beam radiation. On the other hand, the damage caused by this radiation can be repaired by annealing. The target is warmed up to liguid nitrogen temperature for annealing. In addition, the ammonia target has a high ratio of free nucleons (~3/18) approximately 16.5 % for [math]15NH_3[/math] and 26.6 % for [math]15ND_3[/math]. One disadvantage of choosing ammonia is the polarization background caused by 15N(spin - 1/2), or 14N(spin - 1), which was accounted for by taking data using a solid N-15 target.[SChen_FSU_thesis]

Magnet

The 5 T magnetic field produced by a superconducting pair of Helmholtz coils and parallel to the beam direction, provide the hyperfine splittings needed to polarize the target material using ? Ghz RF waves. The uniformity of the field is varying less than [math]10^{-4}[/math] over a cylindrical volume of 20 mm in diameter and length. This configuration is necessary for DNP. The particles with scattering angles between 0-50 are detected in the CLAS as well as 75-105 due to the 8 cm gap between the Helmholtz coils. The target magnetic field does not interact with the electron beam, however it is effective in shielding the drift chambers from the low energy Moller electrons.The target field bents the scattered particles in the azimuthal direction and it falls rapidly with distance as ([math]~ 1/r^3[/math]). The effect of magnetic field at the drift chambers is negligible.[ref 2]

The Evaporation Refrigerator

The target is cooled to ~ 1 K using the helium, which is supplied from the 1 K [math]He^4[/math] evaporation refrigerator. Approximately 0.8 W cooling power is provided by a system of Roots and rotary-vane vacuum pumps that reach a pumping speed for helium gas of 3300 [math]m^3/h[/math][reference 3].

The Target Inserts

The Target Insert

The target insert was designed and built by the INFN of Genova. The target cells with a thickness of 0.2 mm were made out of polychlorotrifluoroethylene (PCTFE), it is a hydrogen-free material and would not produce an NMR background, also it is not effected by radiation as much as other materials. Each target cell is 15 mm in diameter and 10 mm in length sealed by a 0.025 mm thick aluminum foil at entrance window and 0.05 mm thick kapton foil at exit window. [ref 4]
The target insert has the four target cells. Two of them were filled with ammonia beads: the top one with [math]ND_3[/math] and the other one with [math]NH_3[/math]. [math]ND_3[/math] was followed by carbon ([math]C^{12}[/math]) disk with a thickness of 2.3 mm and the fourth cell was left empty. The carbon and the empty cells were used to measure background.[ref 4]
The Nuclear Magnetic Resonance(NMR) coils were wrapped around the outside surface of the cells in order to reduce the background, maximize the amount of ammonia in the target cells and monitor the polarization of the target. The geometry of the NMR coils were chosen so that they would be maximally sensitive to the target polarization. They were made out of CuNi material with a thickness of 0.15 mm and bent into rectangular loops. The temperature sensors(thermocouples, RuO resistors) were attached to the target insert at different locations to monitor the temperature of the target materials.[ref 4]

The N 15 Insert Stick

A second target insert was designed and built by the Jefferson Lab Polarized Target Group to measure the background using solid [math]N^{15}[/math]. The insert cell is made out of a Torlon of 15.7 mm in diameter and 12.7 mm in length. Both sides of the cell are covered by kapton windows. The target cell was filled with isotropically enriched [math]N^{15}[/math] gas at room temperature and the insert was located into the target chamber in order to cool it by LHe, causing the gas to condense. To avert the target from freezing a heater wire was wrapped around the filling tubes and plugging the tubes before the cell was filled with the gas.
The target insert during the experiment is moved up or down using the stepping motor, which means that the target can be changed automatically.[ref 4]

The CEBAF Large Acceptance spectrometer

The CEBAF Large Acceptance spectrometer is a detector at Thomas Jefferson National Accelerator Facility which covers particle detection almost on 360 degree. The detector is divided into six sectors, each of them including a superconducting coil, which produce a toroidal magnetic field along the beam direction. As a charge particle tracking system was used a set of drift chambers divided by three regions, totally consisting of 18 drift chambers. After the drift chamber system the CLAS detector is equipted with Cherenkov counter for seperating electrons from the pions and with scintillators for determination of the Time of Flight of a charge particle. At the end of the detector the particle identification and timing(resolution) is achieved using electromagnetic calorimeters.

• The Torus Magnet

The CLAS Magnet coils

The torus magnet for CLAS detector consists the six superconducting coils located around the beam line in a toroidal geometry, producing the magnetic field in the [math]\varphi[/math] direction. Each magnetic coil defines the sector of detector. So the CLAS detector has six sectors(spectrometer). The system of the magnet is defined in spherical coordinates where the z-axis are along the beam direction and the x and y axis along the horizontal and vertical plane normal to the beam line.
The maximum current for the CLAS magnet is 2860 A, in the forward direction the total magnetic field is 2.5 T-m and at a polar scattering angle with 90 degrees 0.6 T. The magnet itself is around 5 m in diameter and 5 m in length. The coils of the magnet are cooled by liquid helium circulating through cooling tubes to a superconducting temperature of 4.5 K.[[Yelena Alexsandrovna Pork, Measurement of The spin Structure Functions [math]g_1 (x, Q^2)[/math] of The Proton in The resonance Region.]] One can find out the charged particles momentum knowing the trajectory of a particle. In Eg1b experiment, the operated torus values were: 2250, -2250, 1500, -1500.

• Drift Chambers

Two superlayers of Drift chambers each with six hexagonal pattern drift cells

In order to track the charged particles in the EG1b experiment a drift chamber system is used. A drift chamber is a particle tracking detector that measures the drift time of ionization electrons in a gas to calculate the spacial position of an ionizing particle.
The electric field in a drift chamber is produced by the anode(sense wire) and cathode(field wire) wires. The charge particle traveling trough the drift chamber ionizes the gas, producing the electrons that drift to the anodes. After [math]\delta t[/math] time(drift time) electrons are collected at the anode(sense wire) generating the pulse at t time. The distance from the traversing particle to the sense wire can be calculated using the drift time and velocity.
The drift chamber system in CLAS detector is divided into three regions, each consisting six separate chambers(six sectors). Region 1 (R1) chambers are placed closest to the target, where the magnetic filed is low. Region 2 (R2) chambers are in a high magnetic field region, they are located between the magnetic coils. Region 3 (R3) chambers are outside the torus coils and they are largest ones. The drift chambers contain three type of wires stretched between the endplates: sense, guard and field. The endplates are attached to the drift chamber so that the angle the form is equal to 60 degrees. Each drift chamber is subdivided into two separate superlayers. Each superlayer with six layers of drift cells, and each drift cell with one sense wire surrounded by six field wires forming a hexagonal shape([1]). Each superlayer is surrounded by guard wires at a positive potential to stimulate the electric field caused by the drift cells. The sense wire is operated at positive potential and the field wire at negative. In each superlayer the distance between the sense and field wire increases with the radial distance from the target. In R1 the average distance between the sense and field is 0.7 cm, in R2 1.15 cm and in R3 2.0 cm.
The gas used to fill the CLAS drift chamber is a 90 - 10 % mixture of the argon(Ar) and [math]CO_2[/math], where Ar has an ionization gain of [math]~ 10^4[/math]. Inside the drift chamber the constant pressure is provided by outflowing the gas. The chamber endplates are equipped with the circuit board with a single channel differential pre-amplifier for each sense wire.

• Cherenkov detector

The threshold CLAS Cherenkov detector is used to distinguish electrons from pions. The mixture gas used to fill the Cherenkov counter is perfluorobutane [math]C_4 F_{10}[/math] gas at atmospheric pressure. The advantage of Perfluorobutane [math]C_4 F_{10}[/math] gas is its high index of refraction n=1.00153, which results in a high photon yield and the following energy thresholds. The threshold for the Cerenkov radiation can be written as [math]v\gt c/n[/math], or for energies [math]E\gt \gamma \times m[/math], where v is the velocity of charged particle, n index of refraction for the medium, c speed of light and [math]\gamma = \frac{1}{\sqrt{1 - \frac{1}{n^2}}}[/math]. In our case [math]\gamma = 18.098[/math], accordingly one can calculate the energy threshold for different charged particles, for electrons it is 9 MeV and for pions 2.5 GeV.
The Cherenkov detector was designed to maximize the coverage in each of the sectors up to an angle [math]\theta=45[/math] degrees.The CLAS Cherenkov DetectorG. Adamsa, V. Burkertb
As a light collector were used the system of mirrors , the light collecting cones and photomultiplier tubes(PMTs). In the extreme regions of the angular acceptance of the spectrometer the number of detected photoelectrons is too low. To get acceptable efficiency of the detector in these regions photomultiplier tubes were placed. The calibration of the Cherenkov detector is in terms of the collected number of photoelectrons.

• Scintillators

Time of Flight Counters in one sector of CLAS detector

The CEBAF Large Acceptance Spectrometer (CLAS) is equipped with 288 scintillator counters. The purpose of the scintillator is to determine the time of flight for the charged particles and to trigger it in coincidence with another detector system for the particle identification. The time of flight system is built so that time resolution at small polar angles [math]\sigma =120[/math]ps and at angles above 90 degrees [math]\sigma=250[/math]ps. This time resolution helps to discriminate pions and kaons up to 2 GeV/c.

The time of flight system is located between the Cherenkov detectors and electromagnetic calorimeters. The scintillator strips(BC_408) are located perpendicularly to the average particle trajectory with an angular polar coverage of 1.5 degrees. Each sector of The CLAS detector consists of 48 scintillator strips with a thickness of 5.08 cm. The length of the scintillators varies from 30 cm to 450 cm and the width is between 15 cm at small polar angles and 22 cm for the large angles.

• Calorimeter

The CLAS detectur contains 8 modules of electromagnetic calorimeter. A calorimeter is a device that measures the total energy deposited by a crossing particle. They are useful in detecting neutral particles and distinguishing between electrons and hadrons due to their different mechanism of depositing energy. The CLAS calorimeter has three main functions:

One of the six modules of electromagnetic calorimeters in CLAS detector

1) detection of electrons at energies above 0.5 GeV;
2) detection of photons with energies higher than 0.2 GeV;
3) detection of neutrons, with discrimination between photon and neutrons using time-of-flight technique.
6 calorimeter modules of the CLAS detector are placed in each sector in the forward region (polar angle of 10-45 degrees, forward angle calorimeter), while the other two modules are located at large angles in sectors 1 and 2(50-70 degrees, large angle calorimeter). The forward calorimeter has a lead/scintillator thickness ratio 0.2, with 40 cm of scintillators and 8 cm of lead per module. The lead-scintillator sandwich is shaped as a equlaterial triangle in order to match the hexagonal geometry of the CLAS detector. It is made of 39 layers of a 10 mm BC_412 scintillator and lead sheet of thickness of 2.2 mm. Each scintillator layer contains 36 strips parallel to one side of the triangle, with this configuration each orientation is rotated by 120 degrees from another one. This gives three views each containing 13 layers providing stereo information of the location of the energy deposition. To improve hadron identification, there was provided longitudinal sampling of the shower. Each set of 13 layers were subdivided into an inner 5 layers and outer 8 layers stack.

Preliminary Results

The differential cross-section and electron beam asymmetries were measured using the CEBAF Large Acceptance spectrometer (CLAS) at Thomas Jefferson National Lab with a 5.7?? GeV continues electron beam of [math] 1.09209 \times 10^{33} \frac{[ \# of electrons]}{second \times cm^2}[/math] luminosity and polarized target(frozen ammonia) and compared to the E99-107 data.
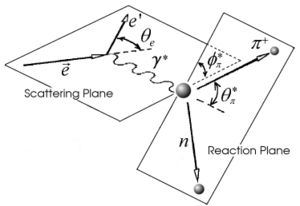
The kinematics of single pion electroproduction can be described by five variables: the virtual photon negative four-momentum transfered squared [math]Q^2[/math], W invariant mass of the photon-nucleon system, [math]{\theta_{\pi}}^*[/math] the polar and [math]{\varphi_{\pi}}^*[/math] the azimuthal angle of the outgoing pion in center of mass frame and [math]{\varphi}_e[/math] the scattered electron azimuthal angle. The four-momentum transfered squared [math]Q^2 = - (k - k^') ^{2} = 4EE^'\sin^2 \frac{\theta_e}{2}[/math], where k(E) nd [math]k^'[/math]([math]E^'[/math]) are the initial and final four-momentum(energy) of the electron in the laboratory frame and [math]\theta_e[/math] - electron scattered angle. The invariant mass [math]W^2 = (P_{\gamma} + P_h)^2 = M_p^2 + 2 M_p \nu + -Q^2[/math], where [math]P_{\gamma}[/math] and [math]P_h[/math] are four-momenta of the virtual photon and target respectively, [math]M_p[/math] is proton mass and [math]\nu = \frac{P_h \cdot P_{\gamma}}{M_p} = E - E^'[/math] the virtual photon energy.

Kinematics of single [math]\pi^+[/math] electroproduction

The five-fold differential cross section can be written in the following way for a single pion electroproduction:

[math]\frac{\partial^5 \sigma}{\partial E_f \partial \Omega_e \partial {\Omega_{\pi}}^*} = \frac{1}{2 \pi} \Sigma \frac{1}{L_{int} A_{cc} \epsilon_{CC} \Delta W \Delta Q^2 \Delta cos {\theta_{\pi}}^* {\phi_{\pi}}^*} \frac{d(W, Q^2)}{d(E_f, cos \theta_e)}[/math]

where [math]\epsilon_{CC} [/math] represents the efficiency of the cherenkov detector, [math]L_{int}[/math] - the integrated luminosity, [math]A_{cc}[/math] is the acceptance factor and the Jacobian term can be expressed in terms of the initial and final energy of lepton:

[math]\frac{d(W, Q^2)}{d(E_f, cos \theta_e)} = \frac{2 M_p E_i E_f}{W}[/math]

Cuts

In the semi-inclusive asymmetry analysis scattered electrons are used. The contamination in the electron sample is removed using the cuts on the energy deposited in the electromagnetic calorimeter, the number of photoelectrons in the Cherenkov counter and fiducial cuts(there should be vertex cut too). the energy deposition in the calorimeter for electrons and pions is different. Pions are minimum ionizing charge particles and energy deposited into the calorimeter, independent of the particles momentum is constant. It is approximately ~ 0.08 GeV. On the other hand, electrons produce photoelectrons and create electromagnetic shower releasing the energy into the calorimeter which is proportional to their momentum. In order to remove contamination due to the energy deposition in the calorimeter the following cut was introduced: [math]EC_{total}\gt 0.2*p[/math]. The cut was also applied to the energy collected in the inner part of the calorimeter: [math]EC_{inner}\gt 0.06*p[/math] , because the ratio of the energy deposited in the total to the inner calorimeter depends on the thickness of the detector and is a constant.

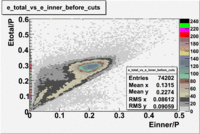
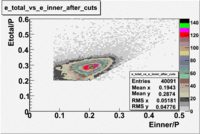
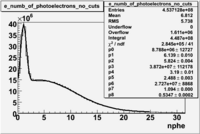
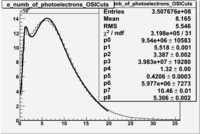
In addition to the cut on the energy deposited into the electromagnetic calorimeter, the misidentified electrons were excluded requiring a signal in the threshold CLAS Cherenkov detector, which is used to distinguish electrons from pions up to 2.5 GeV momentum of the particle. The energy threshold for electrons in the Cherenkov counter is 9 MeV and for pions 2.5 GeV. There are no many pions above 2.5 GeV momentum(should rewrite). A bad recollection of the cherenkov light that occurs for a particular kinematics is responsible for a faulty peak around ~1.5 on the number of photoelectons distribution shown below. To eliminate the faulty peak and high energy pions, which have enough energy to produce photons the geometrical cuts were applied on the data. The second histogram below shows that after cuts the peak around 1.5 disappears. (i need to discuss about nphe>2.5 cut)

No cuts	OSI Cuts
The number of photoelectrons without cuts	The number of photoelectrons with OSI cuts

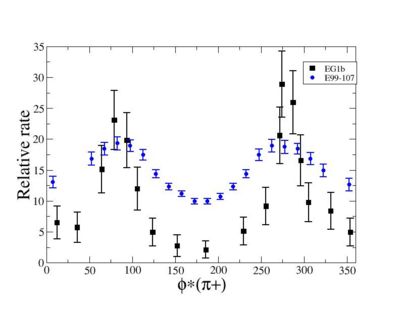
Because of wide range of kinematics, [math]{\varphi_{\pi}}^*[/math] was measured only for certain lepton scattering [math]\theta_e[/math]?? angle and W invariant mass. Applying above described cuts: EC_inner>0.06, EC_tot/p>0.2, nphe>2.5 and [math]0.9\lt M_x\lt 1.1[/math], for he following invariant mass [math]1.44\lt W\lt 1.46[/math] and [math]0.6\lt cos\theta_{pion}^{CM}\lt 0.8[/math] the [math]{\varphi_{\pi}}^*[/math] vs relative rate distribution is shown below on the graph and compared with E99-107 data.

[math]{\varphi_{\pi}}^*[/math] vs Relative rate for fixed [math]cos\theta_{pion}^{CM}=0.7[/math] and [math]W=1.45 GeV[/math]

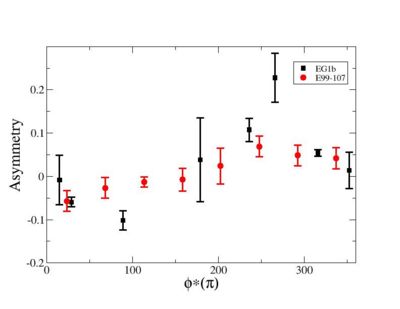
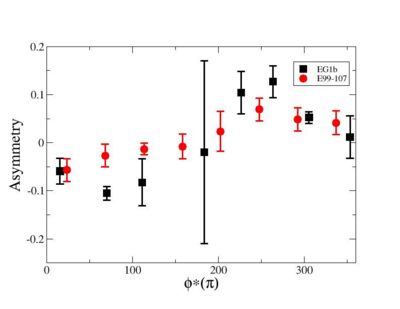
Electron Beam Asymmetry

[math]A = \frac{N^+ - N^-}{N(N^+ - N^-)}[/math]

[math]{\varphi_{\pi}}^*[/math] vs Electron beam helicity asymmetry for [math]W=1.40 GeV[/math] and [math]cos\theta_{pion}^{CM}=0.1[/math]. EG1b compared to E99-107 data [math]{\varphi_{\pi}}^*[/math] vs Electron beam helicity asymmetry for [math]W=1.40 GeV[/math] and [math]cos\theta_{pion}^{CM}=0.1[/math]. EG1b compared to E99-107 data