A kind of analysis

Go Back

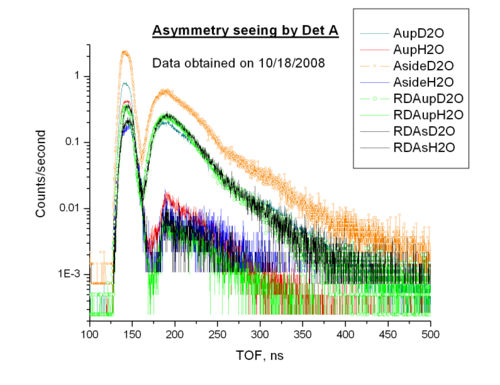
[math]\gamma[/math]-peak positions are shifted w.r.t. each other due to the difference in TOF conversion (electronics amplification). If we wanna calculate the asymmetry as a function of TOF for each channel (neutron energy) it is necessary to match the positions of centroids of [math]\gamma[/math]-peaks. However, one needs to take into account the difference between channel-to-TOF calibration coefficients for each detector.

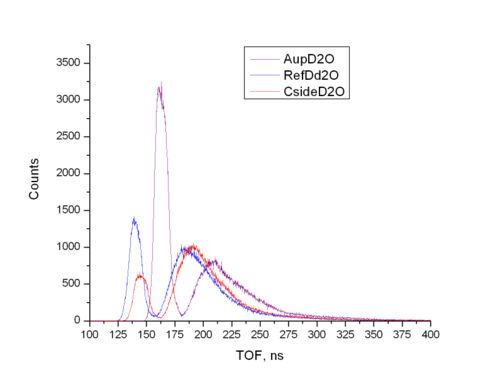
This is what we have if we superimpose TOF-spectra within one plot. It was used used the average channel-to-TOF calibration coefficient (0.179+0.186+0.19)/3 = 0.185 ns/channel (Is it okay to do that?).

Channel-to-TOF calibration coefficients used was 0.19 ns/channel. [math]\gamma[/math]-peak positions were matched manually by cutting out the shift in the spectra w.r.t. Ref Det.

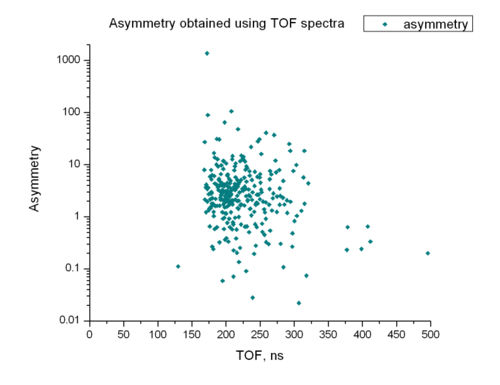
The following plot was drawn using upper plot and formula for calculation of asymmetry placed at [[1]]

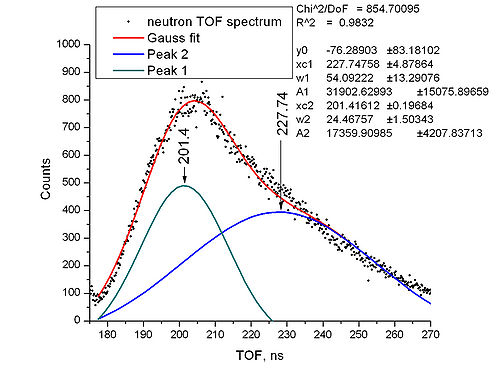
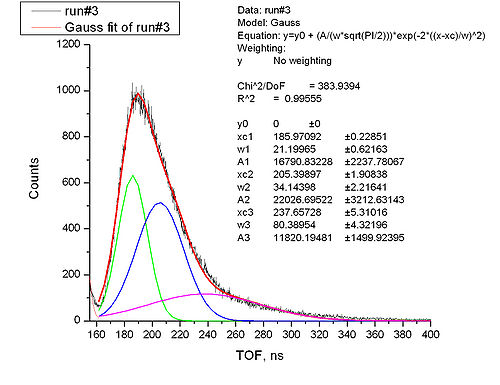
Neutron part of spectrum

We should define how many peaks to use, i.e. we need some physical model for the process we observe.

Why do you want to fit multiple gaussians to the neutron distribution? TF

[math]\frac{N_n}{N_\gamma}[/math] relations

In the calculation of [math]\frac{N_n}{N_\gamma}[/math] it was used just integration of area under the curve instead of fitting neutron spectrum with three peaks (it was observed 0.36% difference between areas calculated in these two ways).

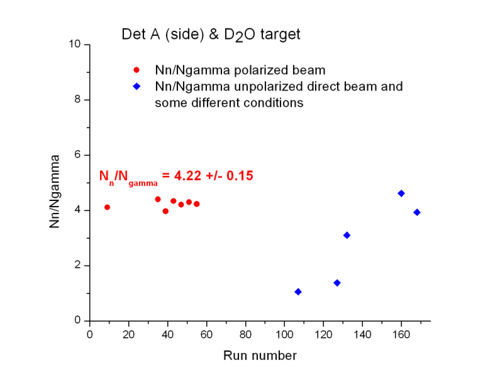
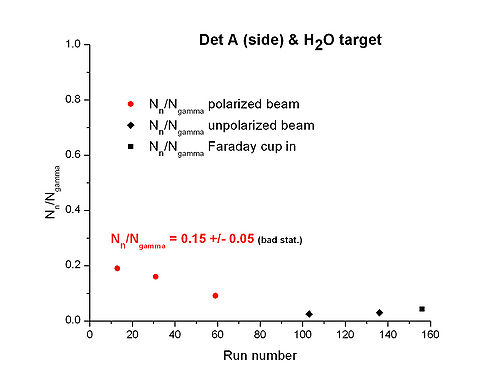
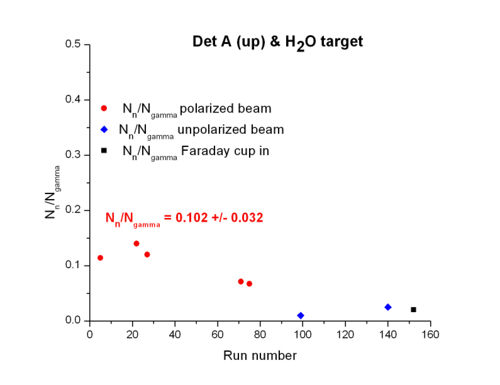
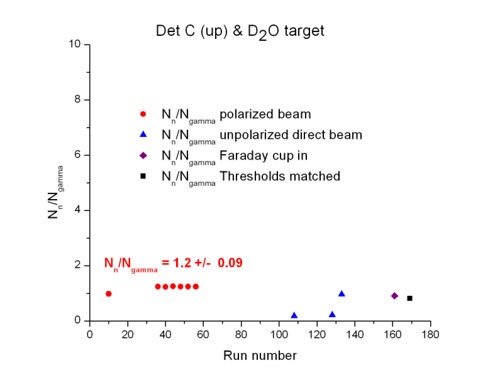
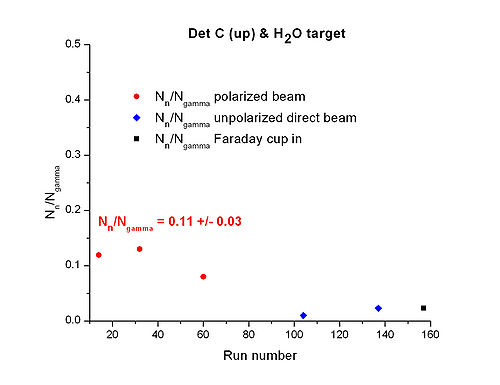
Summary tables for [math]\frac{N_n}{N_\gamma}[/math] averaged over runs w/ polarized beam, [math]D_2O[/math] and [math]H_2O[/math] target

[math]D_2O[/math] target	Det A (side)	Det C (side)	Det A (up)	Det C (up)	Ref Det
<[math]\frac{N_n}{N_\gamma}[/math]>	[math]4.22\pm 0.15[/math]	[math]4.7\pm 0.5[/math]	[math]1.011\pm 0.039[/math]	[math]1.2\pm 0.09[/math]	[math]2.64\pm 0.083[/math]

[math]H_2O[/math] target	Det A (side)	Det C (side)	Det A (up)	Det C (up)	Ref Det
<[math]\frac{N_n}{N_\gamma}[/math]>	[math]0.15\pm 0.05[/math]	[math]0.148\pm 0.042[/math]	[math]0.102\pm 0.032[/math]	[math]0.11\pm 0.03[/math]	[math]0.098\pm 0.025[/math]

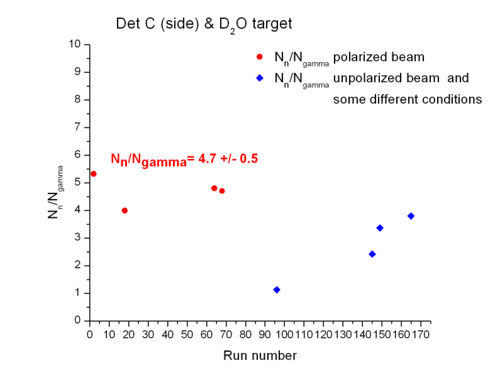
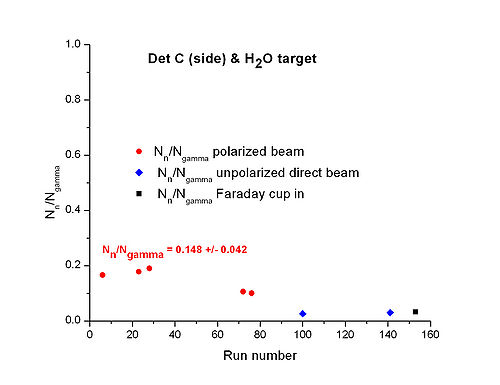
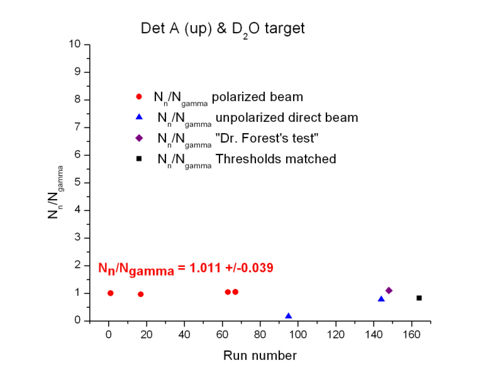
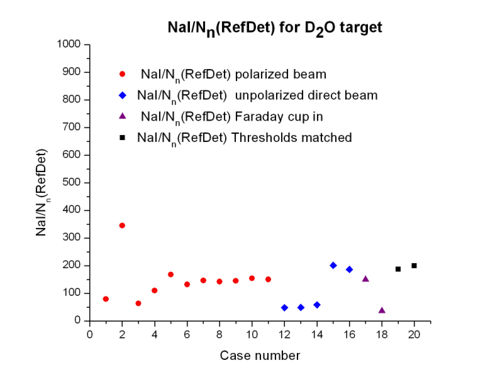
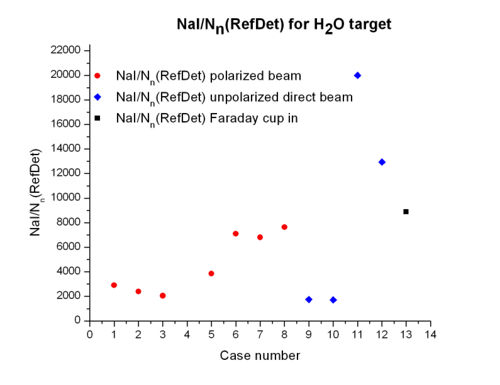
[math]\frac{NaI}{N_\gamma (RefDet)}[/math] relation for [math]D_2O[/math] and [math]H_2O[/math] targets

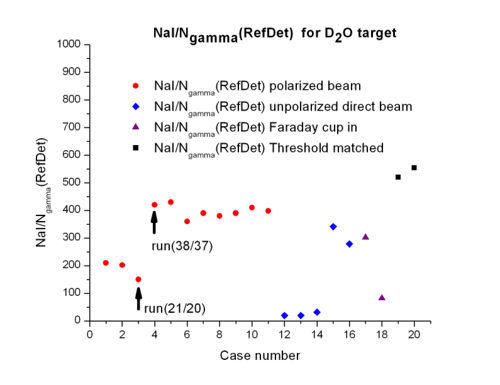
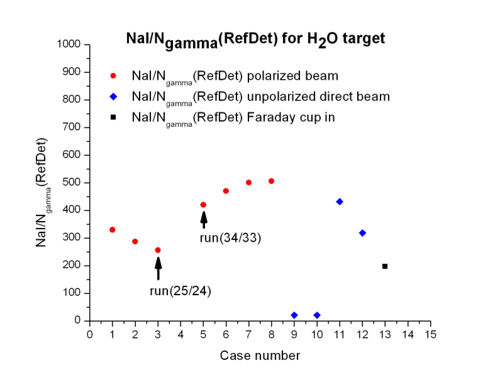
Run(21/20), run(25/24) were taken 10/15/2008 and run(38/37), run(34/33) were carried out on 10/16/2008. Some beam conditions might have been changed.

[math]\frac{NaI}{N_n (RefDet)}[/math] relation for [math]D_2O[/math] and [math]D_2O[/math] targets

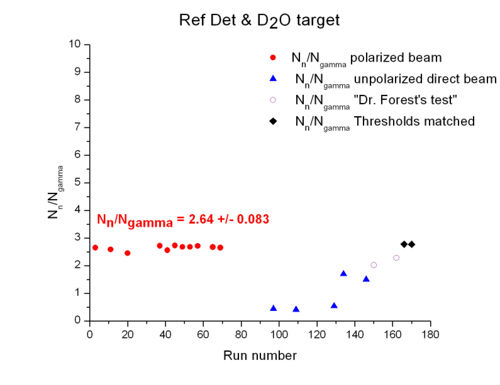
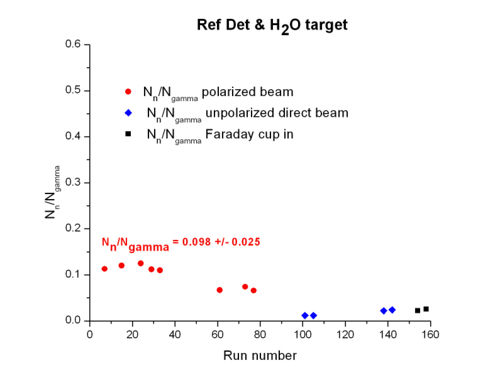
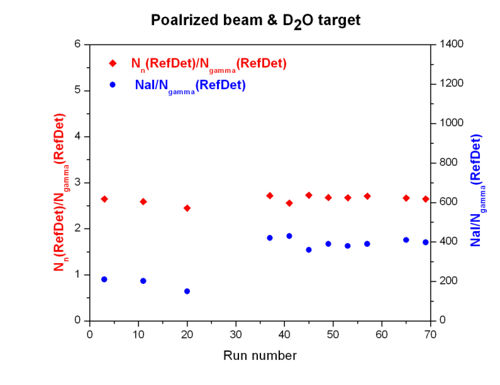
Comparison of [math]\frac{N_n}{N_\gamma}[/math] and [math]\frac{NaI}{N_\gamma}[/math] for Ref Det , [math]D_2O[/math] target, polarized beam

Where do photons come from?

[math]\gamma[/math](MT) = [math]\gamma[/math](Plastic shell)+[math]\gamma[/math](room BKG)

[math]\gamma[/math](H2O target) = [math]\gamma[/math](Plastic shell)+[math]\gamma[/math](H2O liquid)+[math]\gamma[/math](room BKG)

[math]\gamma[/math](MT)
run#	Duration, sec	# of [math]\gamma[/math]'s	Rate ([math]\gamma[/math]/sec)
122 (Det A up)	3071.69	27987.5	9.11
123 (Det C side)	3071.69	14227	4.63
124 (Ref Det)	3071.69	24037	7.825

[math]\gamma[/math](room BKG)
run#	Duration, sec	# of [math]\gamma[/math]'s	Rate ([math]\gamma[/math]/sec)
118 (Det A up)	1812.1	15873.5	8.76
119 (Det C side)	1812.1	7993	4.41
120 (Ref Det)	1812.1	14128	7.796

[math]\gamma[/math](H2O liquid (a))
run#	Duration, sec	# of [math]\gamma[/math]'s	Rate ([math]\gamma[/math]/sec)
118 (Det A up)	1812.1	15873.5	8.76
119 (Det C side)	1812.1	7993	4.41
120 (Ref Det)	1812.1	14128	7.796

Go Back