Effects Due to Target Length

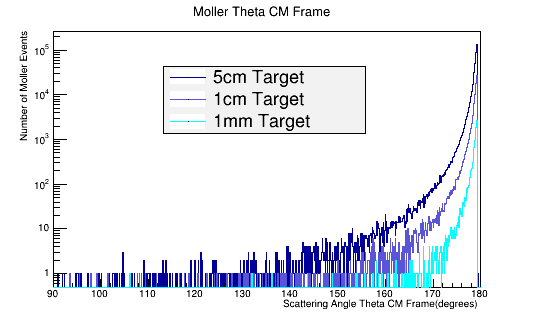
As the target material length is increased, the amount of multiple scattering increases. Since the majority of particles created in the CM frame are at large angles, this implies

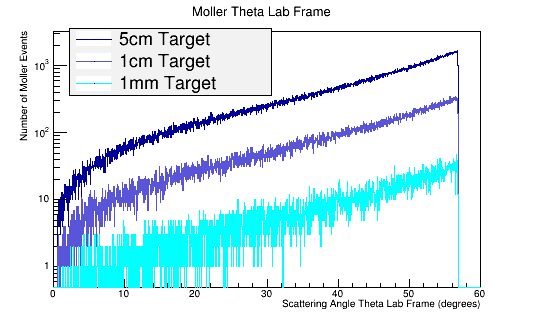
Figure 1: GEANT4 Simulation for the Moller electron scattering angle theta distribution for 6E6 incident 11 GeV electrons in the Lab frame of reference. The LH2 target reduces the mean free path of the Moller electron to around 60 degrees in the lab frame. This property of limiting the Moller angle is independent of the target length.

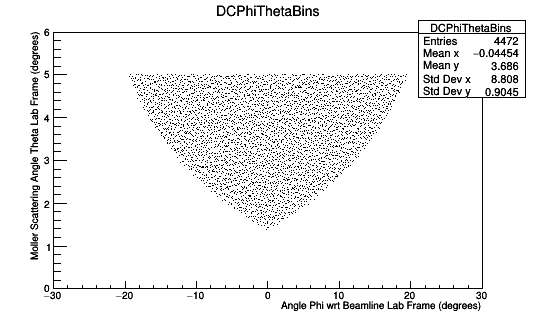
Figure 4a: A plot of the number of Moller scattering angle theta in the lab frame versus the scattering angle phi. The width of the Theta bins is 0.1 degrees in the lab frame within the range of 0 to 6 degrees. Similarly, the width of the Phi bins in 0.2 degrees in the lab frame within the range of -30 to 30 degrees. Only electrons that would have fallen within the range allowed by the DC endplates have been included. Only the DC is simulated with endplates of Tungsten steel.

Figure 3b: A plot of the number of Moller scattering angle theta in the lab frame versus the scattering angle phi. The width of the Theta bins is 0.1 degrees in the lab frame within the range of 0 to 6 degrees. Similarly, the width of the Phi bins in 0.2 degrees in the lab frame within the range of -30 to 30 degrees. Only electrons that would have fallen within the range allowed by the DC endplates have been included. The clas12 setup is simulated without a target.

This gives, for LH2 in a 5cm long target:

[math]\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1m^3}{(100 cm)^3} \times \frac{5 cm}{ } \times \frac{10^{-24} cm^{2}}{barn} =1.05\times 10^{-1} barns^{-1}[/math]

Using the number of incident electrons, for 1 Moller electron:

[math]\frac{1}{\rho_{target}\times l_{target} \times 6\times 10^6}=1.58\times 10^{-6} barns[/math]

This gives, for LH2 in a 1cm long target:

[math]\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1m^3}{(100 cm)^3} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^{2}}{barn} =2.10\times 10^{-2} barns^{-1}[/math]

Using the number of incident electrons, for 1 Moller electron:

[math]\frac{1}{\rho_{target}\times l_{target} \times 6\times 10^6}=7.94\times 10^{-6} barns[/math]

This gives, for LH2 in a 1mm long target:

[math]\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1m^3}{(100 cm)^3} \times \frac{0.1 cm}{ } \times \frac{10^{-24} cm^{2}}{barn} =2.10\times 10^{-3} barns^{-1}[/math]

Using the number of incident electrons, for 1 Moller electron:

[math]\frac{1}{\rho_{target}\times l_{target} \times 6\times 10^6}=7.94\times 10^{-5} barns[/math]