Scattering Cross Section
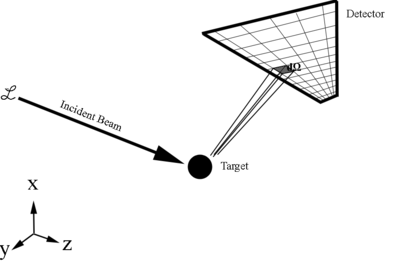
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
[math]\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section[/math]
Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
Luminosity
Luminosity is the quantity that measures the ability of a particle accelerator to produce the required number of interactions and is the proportional to the number of events per second dR/dt and the total cross section σp:
[math]dN=\frac{dR}{dt}=\mathcal L \times \sigma_p[/math]
In order to compute a luminosity for fixed target experiment, it is necessary to take into account the properties of the incoming beam and the stationary target.
[math]\mathcal L = \Phi \rho \ell[/math]
where
[math]\Phi \equiv [/math]flux, or incoming particles per second
[math]\rho \equiv [/math]target density
[math]\ell \equiv [/math]length of target
For the differential cross-section:
[math]\frac{d\sigma}{d\Omega} =\frac{dN}{\mathcal L d\Omega}=\frac{dN}{\Phi \rho \ell d\Omega}[/math]
