LB 170063 Nickel Information With Dead Time

Below is a table with thin windows, original windows, and expanded windows for the nickel on sample 170063. The thin window method can be found at LB Thesis Thin Window Analysis.

	5/25/17	5/26/17	5/27/17	5/29/17	5/30/17	5/31/17	6/1/17
Thin Window
Original Window
Original Background	329.6 +/- 8.6	708.3 +/- 12.8	1611 +/- 19.9	247.4 +/- 7.5	721 +/- 13.1	424.8 +/- 9.9	215.4 +/- 7.0
Integrated Background	659.2 +/- 17.2	1416.6 +/- 25.6	3222 +/- 39.8	494.8 +/- 15	1442 +/- 26.2	849.6 +/- 19.8	430.8 +/- 14
Signal in Thin Window	52350 +/- 228.80	97860 +/- 312.83	118500 +/- 344.24	47420 +/- 217.76	73100 +/- 270.37	54930 +/- 234.37	33720 +/- 183.63
Position on Detector A (cm)	50	30	20	20	10	10	10
Efficiency (Percent)	0.017000 +/- 0.000002	0.042200 +/- 0.000005	0.084700 +/0.000007	0.084700 +/0.000007	0.310000 +/- 0.000003	0.310000 +/- 0.000003	0.310000 +/- 0.000003
Signal in thin Window With Efficiency	307941176.5 +/- 3864757.4	231895734.6 +/- 741812.3	139905549 +/- 406587.1067	55985832.4 +/- 257137.3	23580645.2 +/- 87216.4	17719354.8 +/- 75603. 4	10877419.4 +/- 59235.6
Integrated Background with Efficiency	3877647.1 +/- 101177.5	3372857.1 +/- 60953.7	3804014.2 +/- 46990.42	584179.5 +/- 17709.6	465161.3 +/- 8451.6	274064.5 +/- 6387.1	13897.7 +/- 4516.1
Background Subtracted Signal	304063529.4 +/- 3866081.6	228522877.5 +/- 744312.3	136101534.8 +/- 409293.5	55401652.9 +/- 257746.4	23115483.9 +/- 87624.9	17445290.3 +/- 75872.7	10863521.7 +/- 59407.5
Runtime (s)	301.337	301.322	327.734	300.228	272.845	300.691	306.858
Rate (Hz)	[math] 1.009048 \times 10^6 \pm 1.2829 \times 10^4 [/math]	[math]7.58401 \times 10^5 \pm 2.470 \times 10^3[/math]	[math] 4.15280 \times 10^5 \pm 1.248 \times 10^3 [/math]	[math]1.84531 \times 10^5 \pm 8.58 \times 10^2 [/math]	[math] 8.4720 \times 10^4 \pm 3.2115 \times 10^2[/math]	[math] 5.8017 \times 10^4 \pm 2.5233 \times 10^2 [/math]	[math] 3.5402 \times 10^4 \pm 1.9360 \times 10^2 [/math]
True Rate (Integral Method) (Hz)	[math]1.040020 \times 10^6 \pm 1.3222 \times 10^4 [/math]	[math] 7.81679 \times 10^5 \pm 2.5458 \times 10^3[/math]	[math] 4.29155 \times 10^5 \pm 1.290 \times 10^3 [/math]	[math] 1.90175 \times 10^5 \pm 8.8425 \times 10^2 [/math]	[math] 8.7072 \times 10^4 \pm 3.29 \times 10^2 [/math]	[math] 5.9793 \times 10^4 \pm 2.59 \times 10^2 [/math]	[math] 3.6508 \times 10^4 \pm 2.00 \times 10^2 [/math]
Number of Entries in Histogram	566090	1015134	1428804	541498	984165	761238	494039
[math] \frac{Entries}{Runtime} [/math]	1878.59	3368.93	4359.64	1803.62	3607.05	2531.63	1609.99
Percent Dead	3.95 +/- 0.42	6.59 +/- 0.43	9.09 +/- 0.60	3.95 +/- 0.42	6.59 +/- 0.43	5.06 +/- 0.39	3.06 +/- 0.3
True Rate (Hz)	[math] 1.082790 \times 10^6 \pm 1.4557 \times 10^4 [/math]	[math] 8.36825 \times 10^5 \pm 4.764 \times 10^3 [/math]	[math] 4.72065 \times 10^5 \pm 3.332 \times 10^3[/math]	[math] 1.97995 \times 10^5 \pm 1.322 \times 10^3[/math]	[math] 9.3214 \times 10^4 \pm 5.59 \times 10^2[/math]	[math] 6.2979 \times 10^4 \pm 3.62 \times 10^2 [/math]	[math] 3.7660 \times 10^4 \pm 2.33 \times 10^2 [/math]
.dat file entry	13.90 +/- 0.01	13.64 +/- 0.01	13.06 +/- 0.01	12.20 +/- 0.01	11.44 +/- 0.01	11.04 +/- 0.01	10.54 +/- 0.01

Below is a plot that was made to help find the half life and the initial activity of the sample

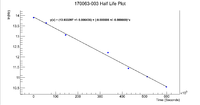
from here we can see that

[math] Slope = 5.63921 \times 10^{-6} \pm 1.75557 \times 10^{-8} [/math]

and the intercept is given by

[math] 13.9333 \pm 0.00643596 [/math]

By exponentiating the intercept, we can find the activity of the nickel foil at the time of the first measurement, which is

[math] 1.125007 \times 10^6 \pm 7.240 \times 10^3 [/math]

Now note that this measurement was taken 8 minutes after the selenium samples were measured. So we must correct the activity back 8 minutes.

[math] A_0 = 1.125007 \times 10^6 \times e^(5.40845 \times 10^{-6} \times \480) = 1.127931 \times 10^6 Hz [/math]

[math] \sigma_{A_0} = 7240 \times e^(5.40845 \times 10^{-6} \times 480) = 7258.82 Hz [/math]