(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Isotropic in CM
Assuming a 1cm long target of LH2 where around 2% of the incident electrons will result in a Moller electron,
TH1F *Combo=new TH1F("Layer1binsMollerRate","Layer1binsMollerRate",113,0,113);
Combo->Add(Layer1binsWeighted,23.8);
Combo->Draw();
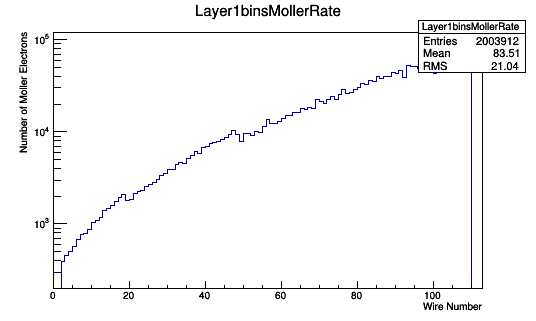
[math]\frac{2003912\ Moller\ Events\ in\ Range}{.30\ Moller\ Events\ in\ Range\ per\ Moller\ Electron}=6.68\times 10^6\ Moller\ electrons[/math]
[math]\frac{6.68\times 10^6\ Moller\ electrons}{.02\ Moller\ Events\ \ per\ Incident\ Electron}=3.34\times 10^8\ Incident\ electrons[/math]
[math]\sigma=\frac{N_{Moller}}{N_{incident}\cdot \rho \ell}=\frac{.02\ barn}{4.2\times 10^{-2}}=.48\ barn[/math]
[math]\mathcal{L}=N_{incident}\ \rho \ell=3.34\times 10^8\ Incident\ electrons \cdot 4.2\times 10^{-2}=\frac{1.40\times 10^{7}\ electrons}{barn \cdot s}[/math]
Assuming a 5cm long target of LH2 where around 2% of the incident electrons will result in a Moller electron,
TH1F *Combo=new TH1F("Layer1binsMollerRate","Layer1binsMollerRate",113,0,113);
Combo->Add(Layer1binsWeighted,4.76);
Combo->Draw();
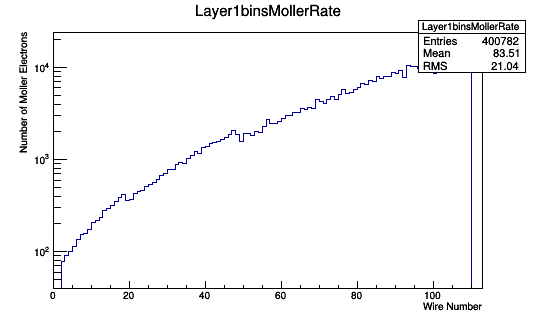
[math]\frac{400782\ Moller\ Events\ in\ Range}{.30\ Moller\ Events\ in\ Range\ per\ Moller\ Electron}=1.34\times 10^6\ Moller\ electrons[/math]
[math]\frac{1.34\times 10^6\ Moller\ electrons}{.02\ Moller\ Events\ \ per\ Incident\ Electron}=6.67\times 10^7\ Incident\ electrons[/math]
[math]\sigma=\frac{N_{Moller}}{N_{incident}\cdot \rho \ell}=\frac{.02\ barn}{2.1\times 10^{-1}}=.095\ barn[/math]
[math]\mathcal{L}=N_{incident}\ \rho \ell=6.67\times 10^7\ Incident\ electrons \cdot 2.1\times 10^{-1}=\frac{1.40\times 10^{7}\ electrons}{barn \cdot s}[/math]
Isotropic in Lab
Assuming a 1cm long target of LH2 where around 2% of the incident electrons will result in a Moller electron,
TH1F *Combo=new TH1F("Layer1binsMollerRate","Layer1binsMollerRate",113,0,113);
Combo->Add(Layer1binsWeighted,23.8);
Combo->Draw();
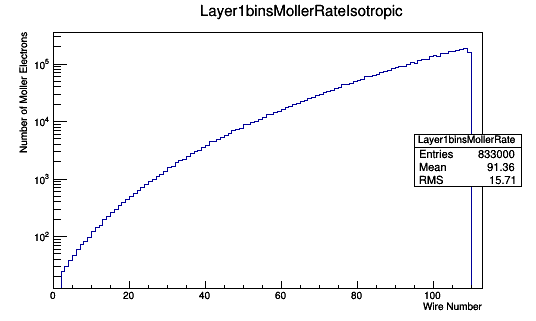
[math]\frac{833000\ Moller\ Events\ in\ Range}{.30\ Moller\ Events\ in\ Range\ per\ Moller\ Electron}=2.78\times 10^6\ Moller\ electrons[/math]
[math]\frac{2.78\times 10^6\ Moller\ electrons}{.02\ Moller\ Events\ \ per\ Incident\ Electron}=1.39\times 10^8\ Incident\ electrons[/math]
[math]\sigma=\frac{N_{Moller}}{N_{incident}\cdot \rho \ell}=\frac{.02\ barn}{4.2\times 10^{-2}}=.48\ barn[/math]
[math]\mathcal{L}=N_{incident}\ \rho \ell=3.34\times 10^8\ Incident\ electrons \cdot 4.2\times 10^{-2}=\frac{5.83\times 10^{6}\ electrons}{barn \cdot s}[/math]
Assuming a 5cm long target of LH2 where around 2% of the incident electrons will result in a Moller electron,
TH1F *Combo=new TH1F("Layer1binsMollerRate","Layer1binsMollerRate",113,0,113);
Combo->Add(Layer1binsWeighted,4.76);
Combo->Draw();
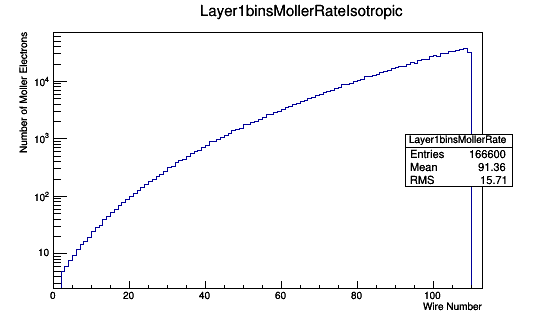
[math]\frac{166600\ Moller\ Events\ in\ Range}{.30\ Moller\ Events\ in\ Range\ per\ Moller\ Electron}=5.55\times 10^5\ Moller\ electrons[/math]
[math]\frac{5.55\times 10^5\ Moller\ electrons}{.02\ Moller\ Events\ \ per\ Incident\ Electron}=2.78\times 10^7\ Incident\ electrons[/math]
[math]\sigma=\frac{N_{Moller}}{N_{incident}\cdot \rho \ell}=\frac{.02\ barn}{2.1\times 10^{-1}}=.095\ barn[/math]
[math]\mathcal{L}=N_{incident}\ \rho \ell=6.67\times 10^7\ Incident\ electrons \cdot 2.1\times 10^{-1}=\frac{5.83\times 10^{6}\ electrons}{barn \cdot s}[/math]



