DC hits to Moller XSection

Verification using LUND and evio files

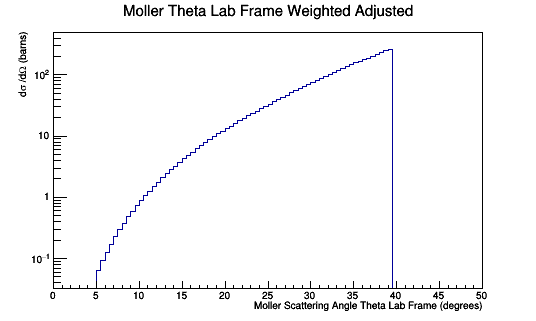
1000 events per degree of 5 to 40 degrees in the Lab Frame

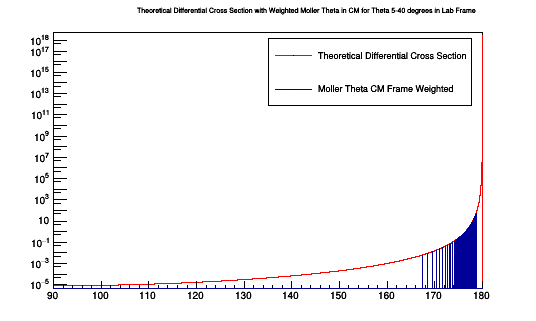
Examing the CM Frame Theta angles which correspond to Lab frame angles within 5-40 degrees, for only on degree in Phi (0 degrees)

For each degree in Theta in the Lab frame, the correct kinematic variables are written to a LUND file 1000 times. These events are read from the evio file using

The Moller Scattering angle Theta is read from the evio file, and it's weight adjusted by dividing by the number it was multiplied by (1000) to give

From the evio file, a histogram can be constructed that will only record the Moller events which result in hits in the drift chamber. A hit for this setting is the procID=90

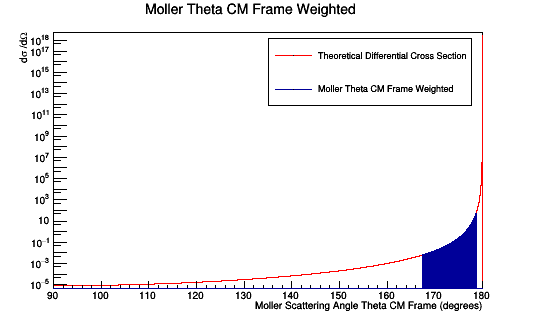
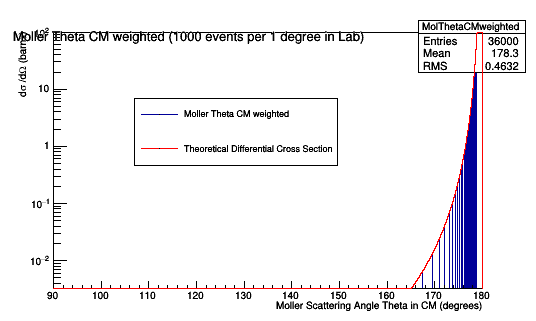
Plotting the Moller scattering angle Theta in the Center of Mass frame just for on occurance of the CM angle gives the Moller Differential Cross-section.

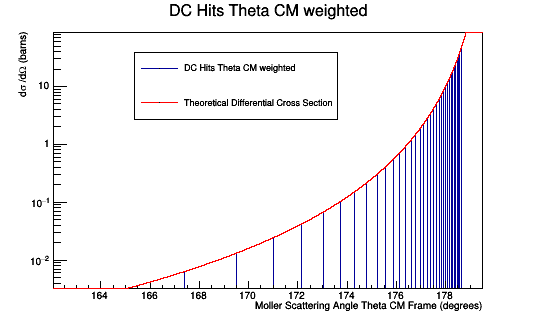
Adjusting the weight by the number of times the specific angle caused hits. We should recover the Moller differential cross-section as found previously.

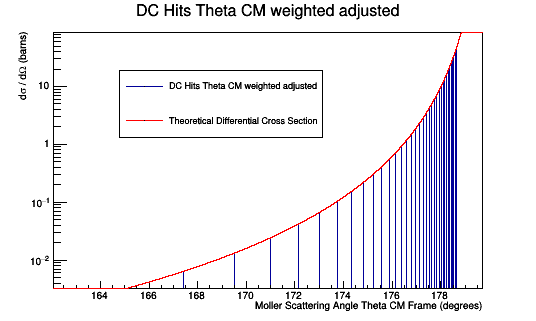
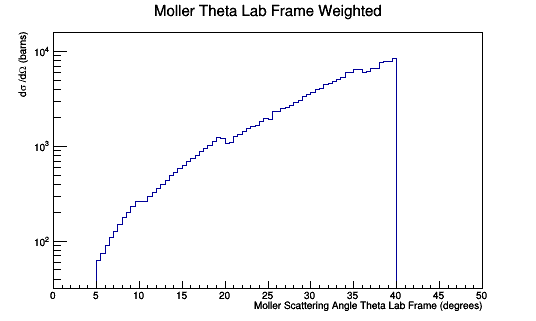
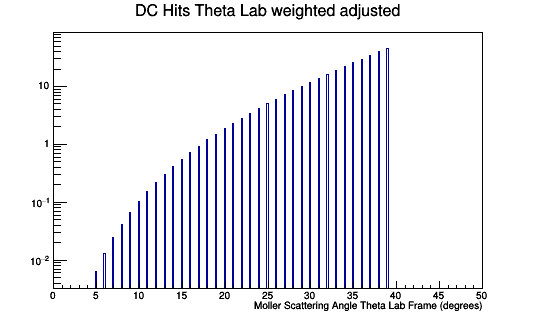
Once the validity of the Moller differential cross-section is established, we can transform from the center of mass to the lab frame as shown earlier. Since the detector is in the lab frame, the hits collected will have to be used to compose a histogram for the Moller scattering angle in the lab frame. We can show that the Moller events that register as hits in the lab matches the Moller differential cross-section in the lab.

Isotropic Spread in CM Frame for 5-40 degrees in Lab

As was done for the situation of 1000 events per degree in the lab frame of reference, the isotropic distribution of scattering angle theta in the center of mass frame can be weighted to reproduce a Moller differential cross-section.

Similarly, as was done earlier, the center of mass frame is transfered to the lab frame.

Since the dimension parallel to the direction of motion "compresses" with speeds approaching the speed of light, the number of events that occur at 5 degrees are different than 40 degrees.  Collecting the number of events that occur within 0.5 degree bin width.

This can be plotted by dividing each entry into the bin by the number of events per that bin and multiplying by the corresponding weight factor.

Determining wire-theta correspondance

To associate the hits with the Moller scattering angle theta, the occupancy plots of the drift chamber hits by means of wire numbers and layer must be translated using the physical constraints of the detector. Using the data released for the DC:

DC: Drift Chambers(specs)

This gives the detector with a working range of 5 to 40 degrees in Theta for the lab frame, with a resolution of 1m radian.

This sets the lower limit:

[math]\frac{5^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.0872664626\ radians[/math]

This sets the upper limit:

[math]\frac{40^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.698131700798\ radians[/math]

Taking the difference,

[math].698131700798-.0872664626\approx\ .61086523198\ radians[/math]

Dividing by 112, we find

[math]\frac{.61086523198}{112}=.005454153912\ radians\approx\ 0.0055\ radians[/math]

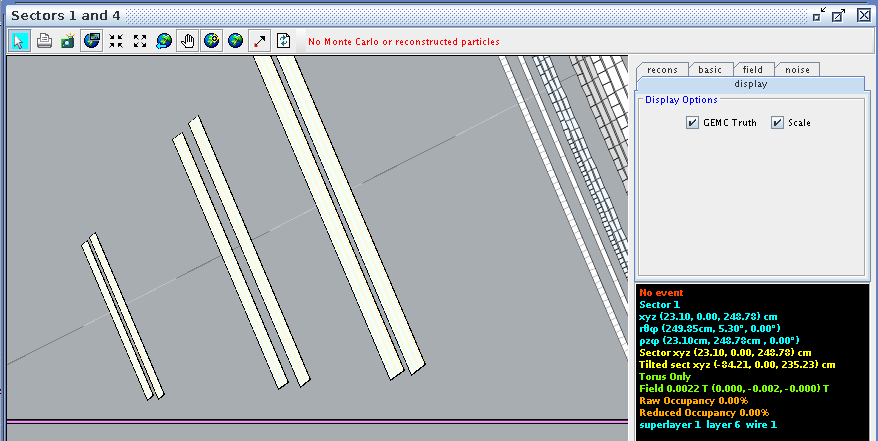
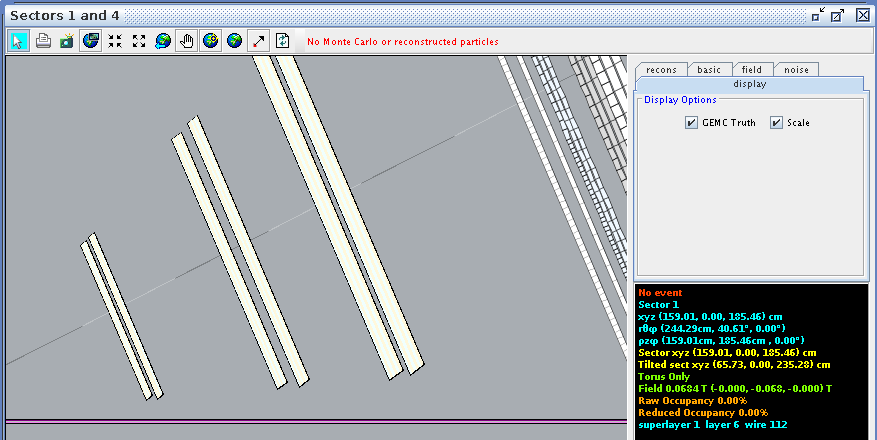
CED Verification

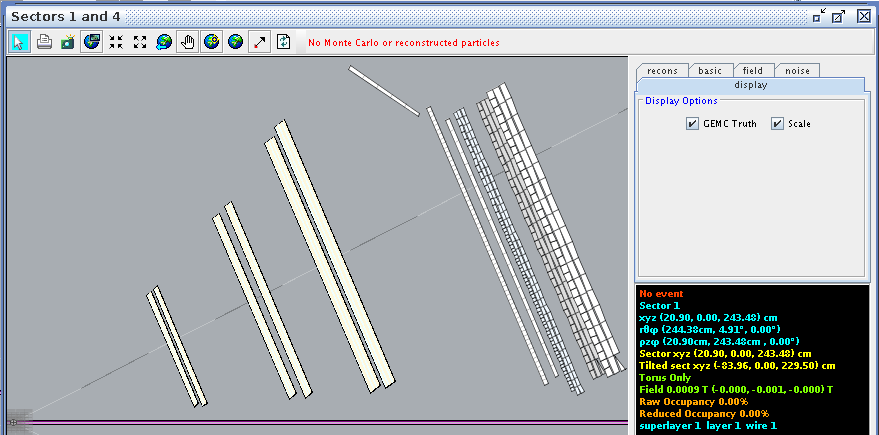
Using CED to verify the angle and wire correlation,

Super Layer 1:Layer 1

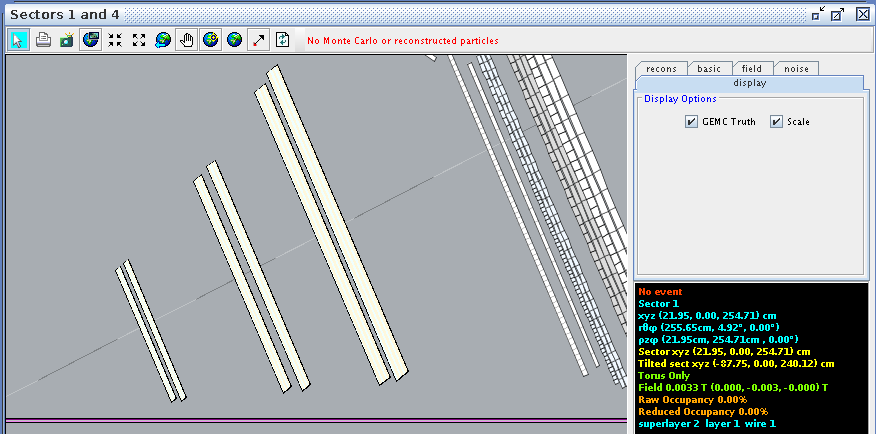
For a hit at layer 1, wire 1 we find the corresponding angle theta in the lab frame to be 4.91 degrees

For a hit at layer 1, wire 2 we find the corresponding angle theta in the lab frame to be 5.19 degrees

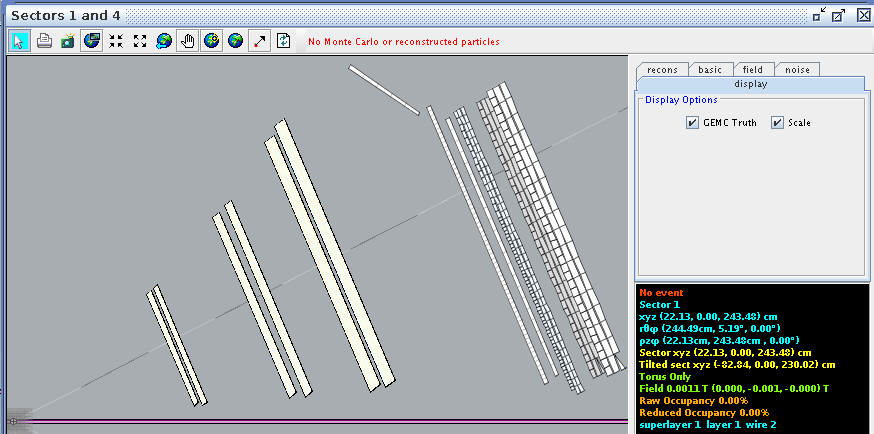
Finding the difference between the two wires,

[math]5.19-4.91=.28^{\circ} \frac{\pi\ radians}{180^{\circ}}=0.004886921906\approx\ 0.00489\ radians[/math]

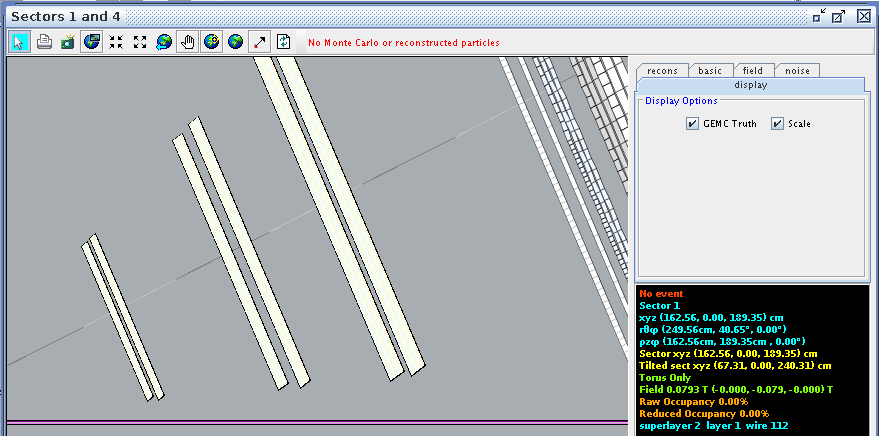
Examing a hit at layer 1, wire 112 we find the corresponding angle theta in the lab frame to be 40.70 degrees

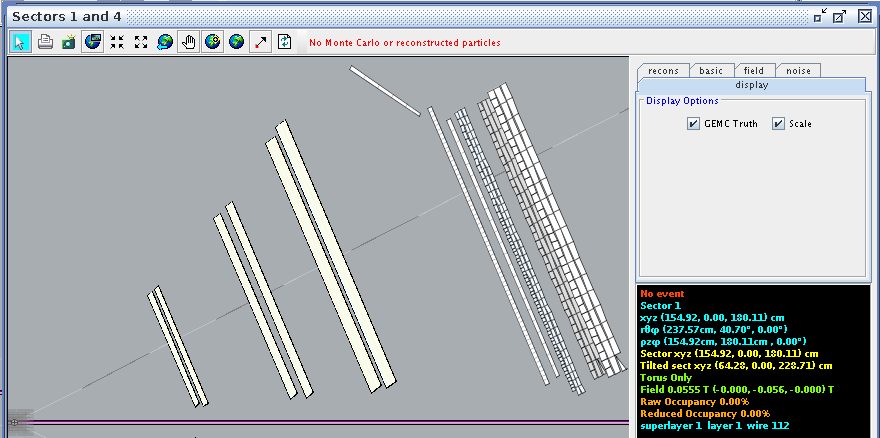
This sets the lower limit:

[math]\frac{4.91^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.085695666273\ radians\approx 0.0857\ radians[/math]

This sets the upper limit:

[math]\frac{40.70^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.710349005562\ radians\approx 0.710\ radians[/math]

Taking the difference,

[math].710349005562-.085695666273\approx\ .625\ radians[/math]

Dividing by 112, we find

[math]\frac{.624653339289}{112}=.005577261958\ radians\approx\ 0.00558\ radians[/math]

Noting the difference from the spacing for a single cell, to the entire detector layer

[math]0.00489-0.00558=0.00069\ \approx .001\ radians[/math]

An uncertainty of this magnitude in radians corresponds to an angular uncertainty of

[math].001\ radian\ \frac{180^{\circ}}{\pi\ radians}\approx .0573^{\circ}[/math]

Testing this for a random angle, 78 degrees we find

[math]0.00558\times 78\ = 0.43524\ radians \frac{180^{\circ}}{\pi\ radians}\approx 24.94^{\circ}[/math]

Adding this to the starting angle of 4.91 degrees

[math]4.91^{\circ}+24.94^{\circ}=29.85^{\circ}\pm .0573^{\circ}[/math]

Comparing this to CED at wire 78

[math]\Longrightarrow 29.85^{\circ}\pm .0573^{\circ}\approx 29.88^{\circ}[/math]

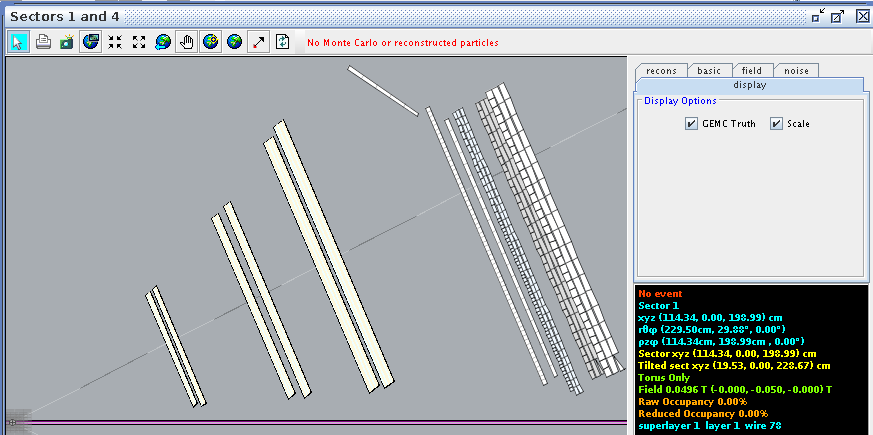
Super Layer 1:Layer 2

For a hit at layer 2, wire 1 we find the corresponding angle theta in the lab frame to be 5.00 degrees

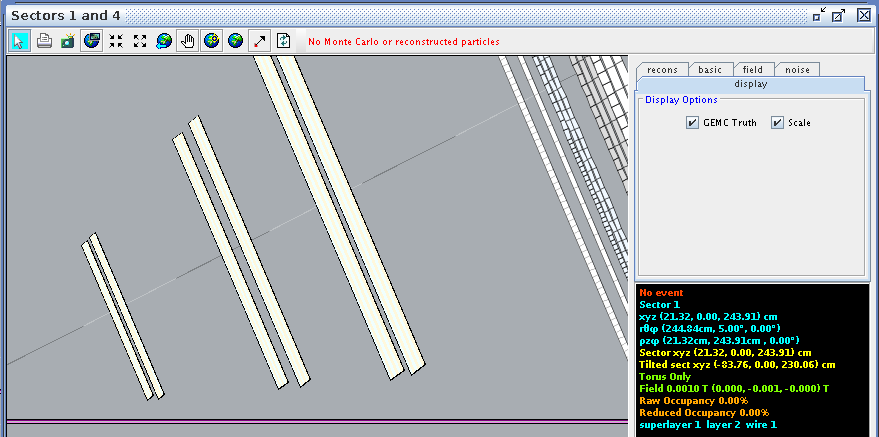
Examing a hit at layer 2, wire 112 we find the corresponding angle theta in the lab frame to be 41.05 degrees

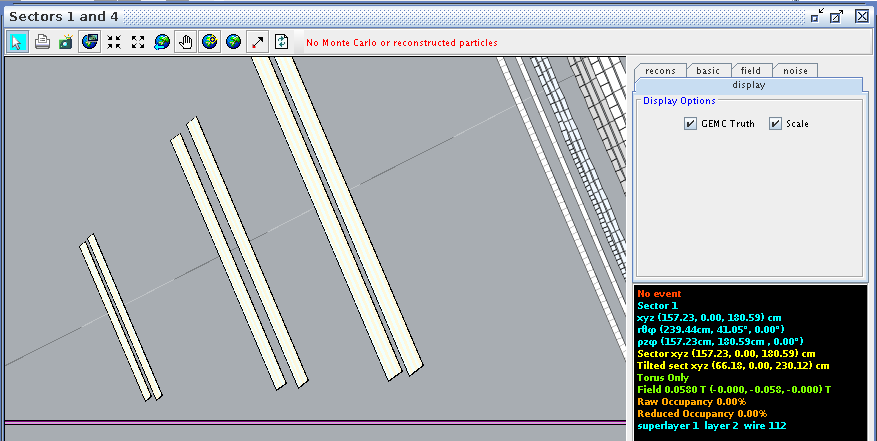
This sets the lower limit:

[math]\frac{5.00^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.0872664626\ radians\approx 0.0873\ radians[/math]

This sets the upper limit:

[math]\frac{40.70^{\circ}}{1}\frac{\pi\ radians}{180^{\circ}}=.716457657944\ radians\approx 0.716\ radians[/math]

Taking the difference,

[math].716457657944-..0872664626\approx\ .629\ radians[/math]

Dividing by 112, we find

[math]\frac{.629191195344}{112}=.00561777853\ radians\approx\ 0.00562\ radians[/math]

Super Layer 1:Layer 6

Superlayer 2:Layer 1