CrossTalk

Go back MCNP simulations

Geometry

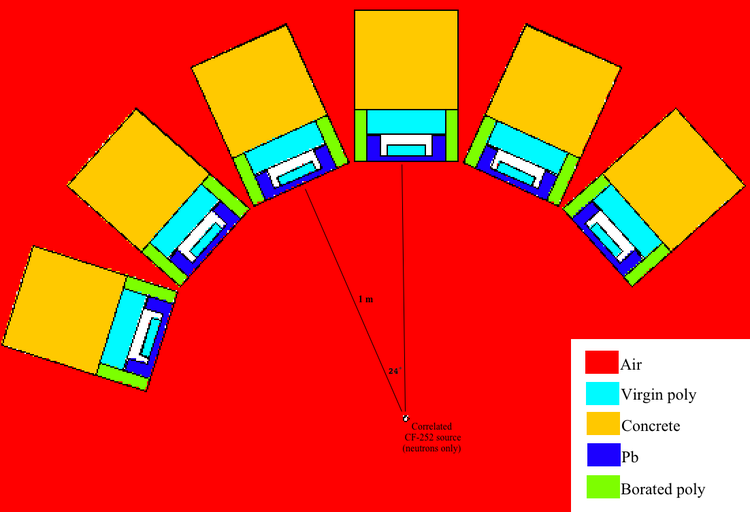
An array of 6 detectors are placed radially at a distance of 1 meter from an uncorrelated 252-CF source. The image below shows a top down view of the simulation geometry. The detector setups have a vertical extent of 30".

Detector physics

The detector physics used in the simulation is MCNP-POLIMI's default treatment for plastic organic scintillators. POLIMI uses electron equivalent light output (MeVee) for simulating detector response. Assuming the detectors have a energy deposition threshold of 0.2 MeV, the corresponding threshold, in electron equivalent light output, becomes 0.03 MeVee.

Summary

Neutron energy deposition from collisions with hydrogen and carbon are converted to electron equivalent light output (MeVee) by MCNP-POLIMI. Neutron collisions that all occur within a pulse collection time of 10 ns of each other are converted to MeVee and cumulated. If the cumulative light output exceeds 0.03 MeVee then it is considered a detection. The value 0.03 MeVee was chosen because it corresponds to a mean neutron energy deposit of 0.2 MeV.

Detector response

The electron equivalent (MeVee) conversion functions for neutrons were measured for plastic (BC 420) scintillators as a function of neutron energy deposit, [math]E_{n}[/math]. For deposit on hydrogen the measurements fit the following quadratic function:

[math]L=0.036E_{n}^{2}+0.125E_{n}[/math]

and for deposit on carbon:

[math]L=0.02E_{n}[/math]

Statistics

The correlation rate will depend on the number of detectors, [math]N[/math], the mean neutron multiplicity, [math]\nu[/math], the fission rate, [math]f[/math], and the probability that a given detector registers a hit from a single source neutron, [math]P_{d}[/math]. [math]P_{d}[/math] is assumed to be the same for all detectors and is calculated from the simulation data as follows: [math]P_{d}=\frac{\text{total number of single hits}}{N*(\text{total number of src neutrons})}[/math]

The n-n correlation rate, [math]R_{nn}[/math], can be estimated as follows:

[math]R_{nn}=f*\nu(\nu-1)*N(N-1)*P_{d}^{2}[/math]

The crosstalk rate, [math]R_{X}[/math] will simply scale proportionally with neutron multiplicity and fission rate. By counting the number of cross talk events directly from the simulation, the estimated crosstalk rate is:

[math]\displaystyle R_{X}=f*\nu*N*P_{X}[/math]

where P_{X} is the probability of crosstalk per source neutron, which is calculated directly from the simulation result:

[math]P_{X}=\frac{\text{total number of cross talk events}}{\text{total number of src neutrons}}[/math]

In order to quantify the amount of crosstalk, I define a 'Signal-to-noise ratio' equal to the ratio between the estimated signal and estimated crosstalk rates.

[math]SNR=\frac{(\nu-1)*(N-1)*P_{d}^{2}}{P_{X}}[/math]

Since I'm uncertain about the neutron multiplicity, I assume it's equal to 2 as a worst case scenario. Go back MCNP simulations