DV Plotting XSect
Jump to navigation
Jump to search
Creating a program called MollerDiffXSect.c
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
main()
{
float angle,dSigma_dOmega;
double alpha=7.2973525664e-3;
double E_CM=53e6; //CM E for 11GeV incident electrons
/* using equation from Landau-Lifshitz & Azfar */
/* units in MeV */
for(angle=90;angle<=180; angle=angle+.5)
// for(angle=90;angle<=180; angle=angle+1)
{
dSigma_dOmega=(alpha*(3+cos(angle*3.14159265359/180)*cos(angle*3.14159265359/180)));
dSigma_dOmega=dSigma_dOmega*dSigma_dOmega;
dSigma_dOmega=dSigma_dOmega/(4*E_CM*E_CM*sin(angle*3.14159265359/180)*sin(angle*3.14159265359/180)
*sin(angle*3.14159265359/180)*sin(angle*3.14159265359/180));
dSigma_dOmega=dSigma_dOmega*1e18;
dSigma_dOmega=dSigma_dOmega*.3892e-3; //barns
dSigma_dOmega=dSigma_dOmega/2; //2 electrons for LH2
fprintf(stdout," %f\t%f\n", angle, dSigma_dOmega);
}
}
Creating a Makefile with contents:
CC = gcc
DiffXSect: MollerDiffXSect.o
$(CC) $(CFLAGS) MollerDiffXSect.o -lm -o DiffXSect
MollerDiffXSect.o: MollerDiffXSect.c
$(CC) $(CFLAGS) -c MollerDiffXSect.c
The program can be run with the commands:
make DiffXSect ./DiffXSect >DiffXSect.dat
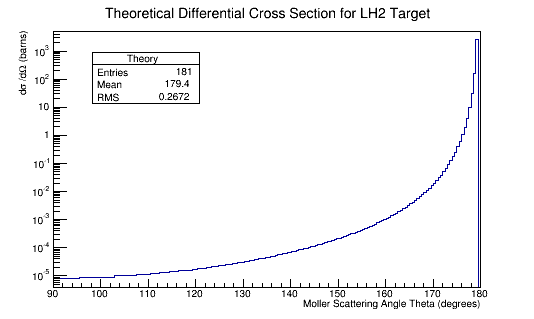
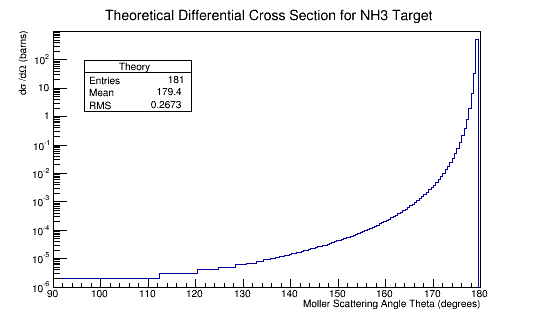
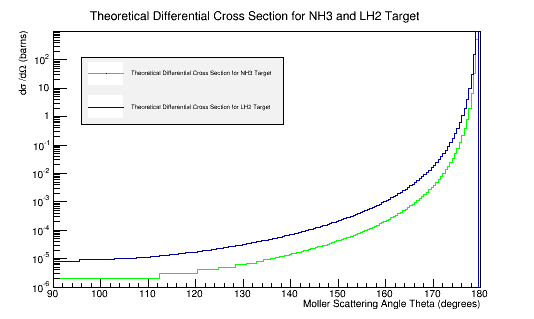
This creates a data file with the scattering angle theta and the corresponding theoretical Moller differential cross-section for said angle.
A data file is created with the differential cross-section for the scattering angle theta, by increments of .5 degrees
90.000000 0.000008 90.500000 0.000008 91.000000 0.000008 91.500000 0.000008 92.000000 0.000008 92.500000 0.000008 93.000000 0.000008 93.500000 0.000008 94.000000 0.000008 94.500000 0.000008 95.000000 0.000008 95.500000 0.000009 96.000000 0.000009 96.500000 0.000009 97.000000 0.000009 97.500000 0.000009 98.000000 0.000009 98.500000 0.000009 99.000000 0.000009 99.500000 0.000009 100.000000 0.000009 100.500000 0.000009 101.000000 0.000009 101.500000 0.000009 102.000000 0.000009 102.500000 0.000009 103.000000 0.000010 103.500000 0.000010 104.000000 0.000010 104.500000 0.000010 105.000000 0.000010 105.500000 0.000010 106.000000 0.000010 106.500000 0.000010 107.000000 0.000010 107.500000 0.000011 108.000000 0.000011 108.500000 0.000011 109.000000 0.000011 109.500000 0.000011 110.000000 0.000011 110.500000 0.000012 111.000000 0.000012 111.500000 0.000012 112.000000 0.000012 112.500000 0.000013 113.000000 0.000013 113.500000 0.000013 114.000000 0.000013 114.500000 0.000014 115.000000 0.000014 115.500000 0.000014 116.000000 0.000014 116.500000 0.000015 117.000000 0.000015 117.500000 0.000015 118.000000 0.000016 118.500000 0.000016 119.000000 0.000016 119.500000 0.000017 120.000000 0.000017 120.500000 0.000018 121.000000 0.000018 121.500000 0.000019 122.000000 0.000019 122.500000 0.000020 123.000000 0.000020 123.500000 0.000021 124.000000 0.000021 124.500000 0.000022 125.000000 0.000023 125.500000 0.000023 126.000000 0.000024 126.500000 0.000025 127.000000 0.000026 127.500000 0.000026 128.000000 0.000027 128.500000 0.000028 129.000000 0.000029 129.500000 0.000030 130.000000 0.000031 130.500000 0.000032 131.000000 0.000033 131.500000 0.000035 132.000000 0.000036 132.500000 0.000037 133.000000 0.000039 133.500000 0.000040 134.000000 0.000042 134.500000 0.000043 135.000000 0.000045 135.500000 0.000047 136.000000 0.000049 136.500000 0.000051 137.000000 0.000053 137.500000 0.000056 138.000000 0.000058 138.500000 0.000061 139.000000 0.000063 139.500000 0.000066 140.000000 0.000070 140.500000 0.000073 141.000000 0.000076 141.500000 0.000080 142.000000 0.000084 142.500000 0.000088 143.000000 0.000093 143.500000 0.000098 144.000000 0.000103 144.500000 0.000109 145.000000 0.000115 145.500000 0.000121 146.000000 0.000128 146.500000 0.000136 147.000000 0.000144 147.500000 0.000152 148.000000 0.000162 148.500000 0.000172 149.000000 0.000183 149.500000 0.000195 150.000000 0.000208 150.500000 0.000221 151.000000 0.000237 151.500000 0.000253 152.000000 0.000271 152.500000 0.000291 153.000000 0.000312 153.500000 0.000336 154.000000 0.000362 154.500000 0.000391 155.000000 0.000422 155.500000 0.000457 156.000000 0.000495 156.500000 0.000538 157.000000 0.000586 157.500000 0.000639 158.000000 0.000698 158.500000 0.000764 159.000000 0.000838 159.500000 0.000922 160.000000 0.001016 160.500000 0.001123 161.000000 0.001245 161.500000 0.001383 162.000000 0.001542 162.500000 0.001724 163.000000 0.001934 163.500000 0.002177 164.000000 0.002460 164.500000 0.002791 165.000000 0.003179 165.500000 0.003638 166.000000 0.004183 166.500000 0.004834 167.000000 0.005618 167.500000 0.006568 168.000000 0.007727 168.500000 0.009156 169.000000 0.010931 169.500000 0.013159 170.000000 0.015986 170.500000 0.019616 171.000000 0.024340 171.500000 0.030579 172.000000 0.038953 172.500000 0.050406 173.000000 0.066401 173.500000 0.089281 174.000000 0.122933 174.500000 0.174058 175.000000 0.254769 175.500000 0.388214 176.000000 0.621708 176.500000 1.060403 177.000000 1.964202 177.500000 4.072398 178.000000 9.941240 178.500000 31.416433 179.000000 159.035599 179.500000 2544.472656 180.000000 inf
A c++ macro can be written to input this into root
root -l MollerDiffXSect2Root()
void MollerDiffXSect2Root()
{
struct evt_t
{
Int_t event;
Float_t Angle, dSigma_dOmega;
};
ifstream in;
in.open("DiffXSect.dat");
evt_t evt;
Int_t nlines=0;
TFile *f = new TFile("DiffXSect.root","RECREATE");
TTree *tree = new TTree("DiffXSect","Moller Diff Xsect");
TH1F *Th=new TH1F("Theory","Theoretical Differential Cross Section",181,90,180);
tree->Branch("evt",&evt.event,"event/F:Angle/F:dSigma_dOmega");
while(in.good())
{
evt.event=nlines;
in >> evt.Angle >> evt.dSigma_dOmega;
nlines++;
tree->Fill();
Th->Fill(evt.Angle,evt.dSigma_dOmega);
}
tree->Print();
tree->Write();
f->Write();
in.close();
delete tree;
delete f;
}


