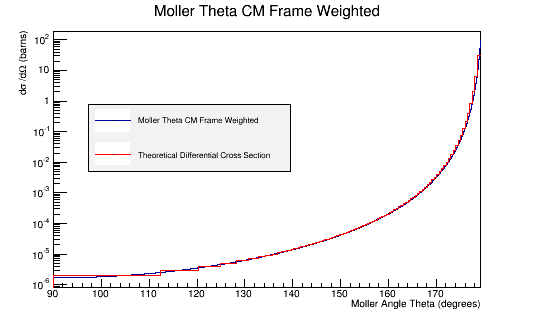
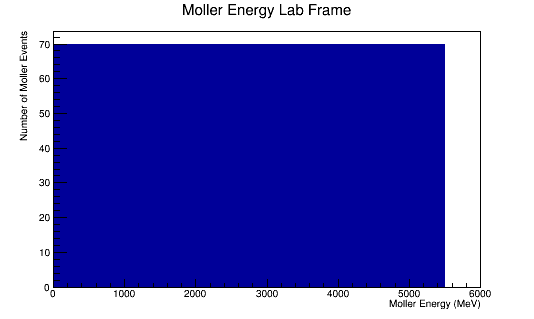
Uniform distribution in Energy and Theta LUND files

File:LUND Spread.C

The LUND file is created by creating an isotropic distribution of particles within the energy range of 2MeV-5.5GeV as is found through GEANT simulation. These particles are also uniformly distributed through the angle theta with respect to the beam line in the range 5-40 degrees. This is done at a set angle phi (10 degrees) with respect to the perpendicular components with respect to the beam line.

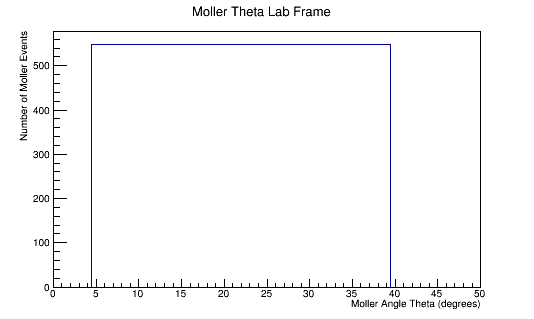
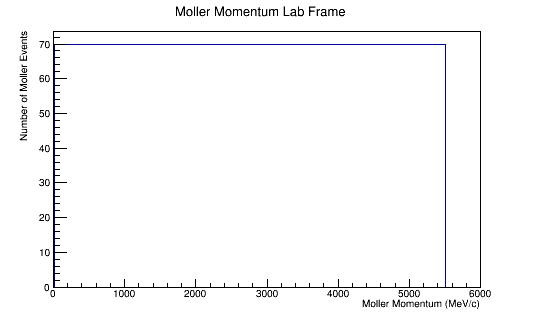
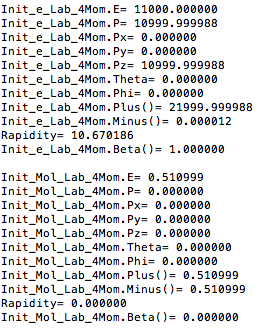
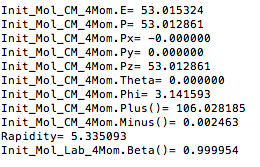
Center of Mass for Stationary Target

For an incoming electron of 11GeV striking a stationary electron we would expect:

Boosting to the Center of Mass Frame:

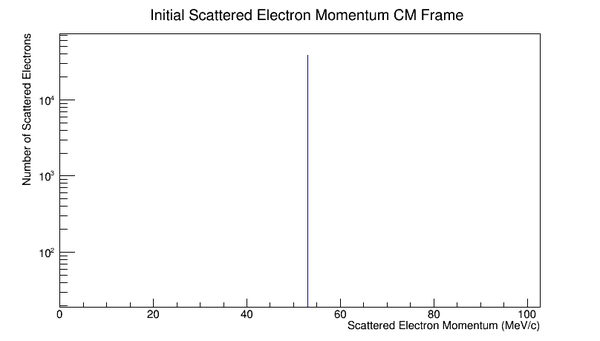
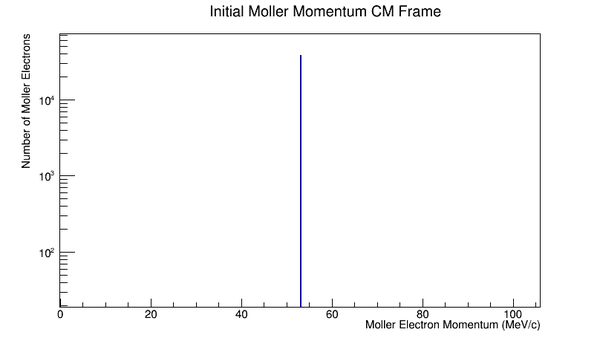
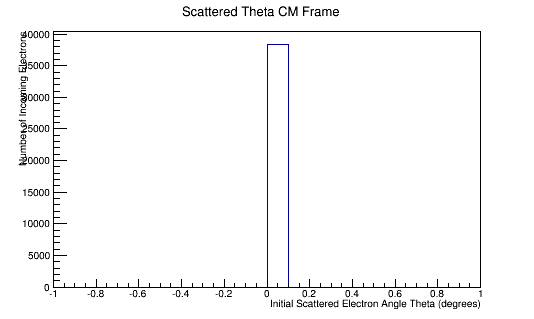
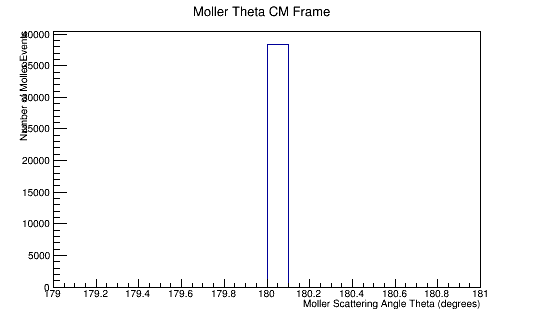
Phase space Limiting Particles

Since the angle phi has been constrained to remain constant, the x and y components of the momentum will increase in the positive first quadrant. This implies that the z component of the momentum must decrease by the relation:

[math]p^2=p_x^2+p_y^2+p_z^2[/math]

In the Center of Mass frame, this becomes:

[math]p_x^{*2}+p_y^{*2} = p^{*2}-p_z^{*2}[/math]

Since the momentum in the CM frame is a constant, this implies that pz must decrease. For phi=10 degrees:

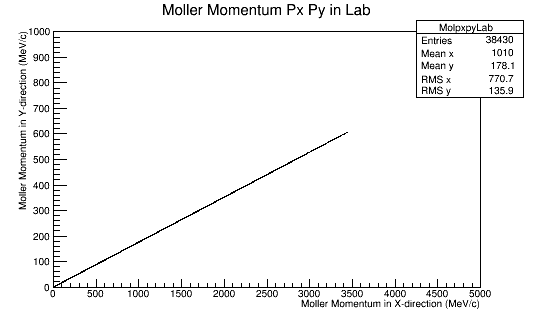
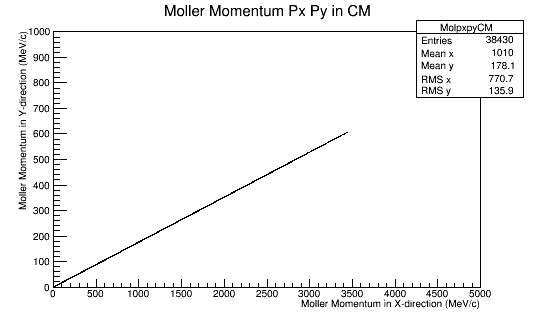
This is repeated for rotations of 60 degrees in phi in the Lab frame.

We can use the variable rapidity:

[math]y \equiv \frac {1}{2} \ln \left(\frac{E+p_z}{E-p_z}\right)[/math]

where

[math] P^+ \equiv E+p_z[/math] [math] P^- \equiv E-p_z[/math]

this implies that as

[math]p_z \rightarrow 0 \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow 1 \Rrightarrow \ln 1 \rightarrow 0 \Rrightarrow y=0[/math]

For forward travel in the light cone:

[math]p_z \rightarrow E \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow \infin \Rrightarrow \ln \infin \rightarrow \infin \Rrightarrow y \rightarrow \infin [/math]

For backward travel in the light cone:

[math]p_z \rightarrow -E \Rrightarrow \frac{E+p_z}{E-p_z} \rightarrow 0 \Rrightarrow \ln 0 \rightarrow -\infin \Rrightarrow y \rightarrow -\infin [/math]

For a particle that transforms from the Lab frame to the CM frame where the particle is not within the light cone:

[math]p_x^2+p_y^2=52.589054^2+9.272868^2=53.400MeV \gt 53.015 MeV (E) \therefore p_z \rightarrow imaginary[/math]

These particles are outside the light cone and are more timelike, thus not visible in normal space. This will reduce the number of particles that will be detected.

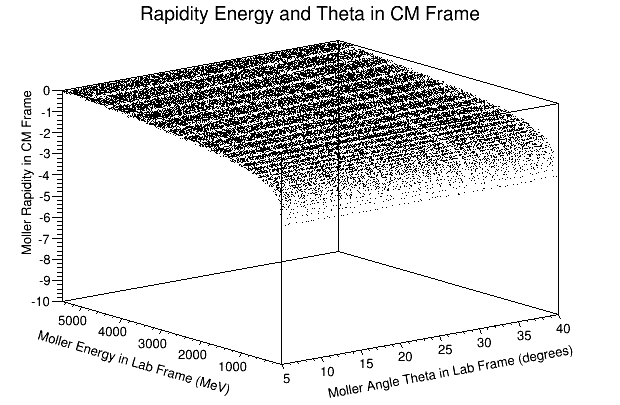
Using Initial Condition based on After Collision in Lab Frame

Starting with an initial Energy (10MeV), an initial angle Theta (5 degrees),and a Phi angle of 10 degrees, the 4-momentum vector can be kinematically determined:

[math]E=\sqrt{p^2+m^2}\Rightarrow p=\sqrt{E^2-m^2} \Rightarrow p=\sqrt{100MeV^2-.2611MeV^2}=9.9869MeV/c[/math]

Using the fact that the angle Theta is defined to be in the xz plane:

[math]P_z=P\ Cos{\theta}=(9.9869MeV/c )Cos{5}=9.9489 MeV/c[/math]

Using the fact that phi is defined in the xy plane to be:

[math]P_{xy}=\sqrt{P^2-P_z^2}\Rightarrow P_x=P_{xy} Cos{\phi}=(.8704 MeV/c) Cos{10}=.8572MeV/c[/math]

[math]P_y=\sqrt{P^2-P_x^2-P_z^2}=.1509MeV/c[/math]

Using Conservation of Energy, the scattered electron energy and momentum after the collision in the lab frame can be found using the 4-momentum vectors:

[math]\mathbf{P}_{scattered}=\mathbf{P}_{Lab}-\mathbf{P}_{Moller}[/math]

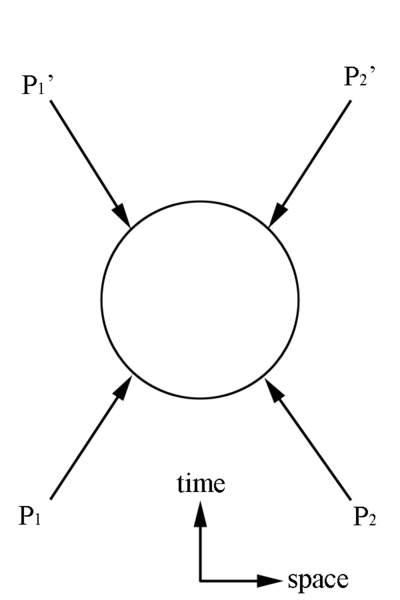
We can use that fact that initial electron was the only source of momentum in the lab frame before the collision, and use the Mandelstram variable u

[math]\Longrightarrow \left({\mathbf P_1^*}- {\mathbf P_2^{'*}}\right)^2=\left({\mathbf P_2^*}- {\mathbf P_1^{'*}}\right)^2\equiv u[/math]

For the Energy:

[math]\Longrightarrow \left({11000MeV}- {10MeV}\right)^2=\left({.511MeV}- {\mathbf P_^{'scattered}}\right)^2\equiv u[/math]

For the Momentum:

[math]\Longrightarrow \left({10999.9999881MeV/c}- {9.9869MeV/c}\right)^2=\left({0}- \mathbf {P}_{scattered}\right)^2\equiv u[/math]

[math]\Longrightarrow \left({10999.9999881MeV/c}- {9.9869MeV/c}\right)^2=\left({10990.0130881MeV/c}\right)^2\equiv u[/math]

[math]\Rightarrow \sqrt{u}=10990.0130881MeV/c[/math]

Using Initial Condition based on After Collision in CM Frame

We can use the Mandelstram variable s, which is a Lorentz invariant, to find the energy in the center of mass frame where the total momentum is zero.

[math]s={\mathbf P}^2=(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2=(m_{1}+m_{2})^2=(E_{1}^*+E_{2}^*)^2\Rightarrow E^*=\sqrt{s}=106.03MeV[/math]

Since the two particles are identical mass, this implies that they should have equal energy in the Center of Mass frame:

[math](E_{1}^*+E_{2}^*)=E^*\Rightarrow E_1^*=E_2^*=53.015MeV[/math]

Momentum in this frame can be found using the relativistic expression for energy

[math]E^2=P^2+m^2\Rightarrow P_1^*=\sqrt{E_1^*-m^2}=53.013MeV/c[/math]

Since only the z component is affected by the Lorentz transformation, we know that the x and y components will remain the same in both the lab frame and Center of Mass frame.

[math]P_x=P_x^*[/math] [math]P_y=P_y^*[/math]

We can determine the z component with

[math]P_z^*=\sqrt{P^{*2}-P_x^{*2}-P_y^{*2}}=\pm 53.006 MeV/c[/math]