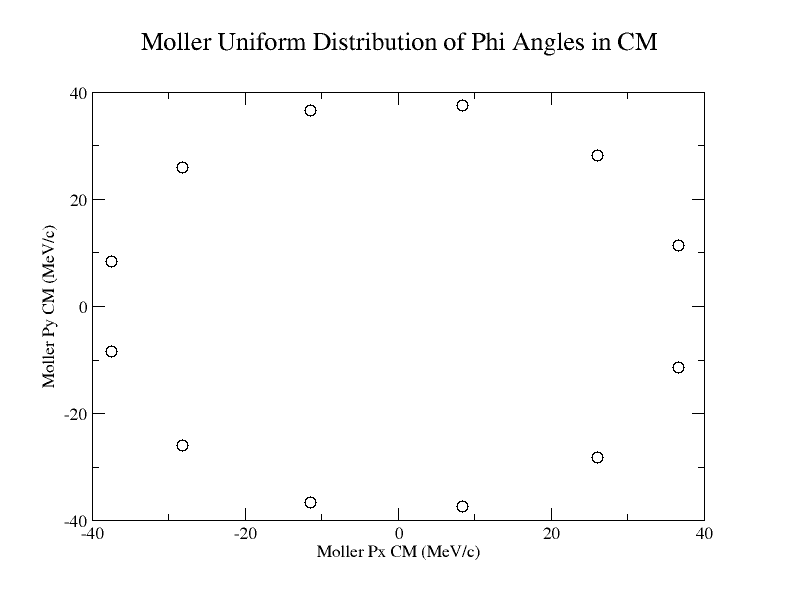
Calculations of 4-momentum components
Setup
Since we want to run for a evenly spaced energy range for Moller electrons, we will need to use some of the scattered electrons to help cover this range. A Moller scattering data file of 4E7 events has no Moller electrons with momentum over 5500 MeV.
awk 'NR == 1 {line = $0; max = $15} NR >1 && $15 > max {line =$0; max =$15} END{print line}' MollerScattering_NH3_4e7incidnet.dat
11000 0 0 11000.5 0 0 -510 5502.94 -14.7812 -50.9086 5503.19 0 0 -505.319 5495.8 14.7812 50.9086 5496.06 0 0 -505.319
Since momentum is conserved, and the data is verified kinematicly, we cannot simply "switch" the data. This data can be altered to have a certain number of different phi values for each energy to match the Moller cross section. This data can then be written to a LUND file, and compared to the previous calculations which did not factor in loss of initial energy.
Prepare Data
Using the existing Moller scattering data from a GEANT simulation of 4E8 incident electrons, a file of just scattered momentum components can be constructed using:
awk '{print $9, $10, $11, $16, $17, $18}' MollerScattering_NH3_4e8incident.dat > Just_Scattered_Momentum.dat
Transfer to CM Frame
Reading in the data from the dat file, we use a C++ program to read the momentum components for the Scattered and Moller electrons into 4-momentum vectors defined as the Lab_final frame of reference.
Performing a Lorentz boost to a Center of Mass frame for the two 4-vectors from the Lab_final frame of reference, we move to a frame where the energies are equal and the momentum are equal but opposite.
Relativistic Kinematics
For Moller Electron energies above 500 MeV, in the Lab frame, histograms of momentum, and theta as well as a 2-D histogram of Energy vs. Theta for the Moller Electron in the CM frame will be filled.
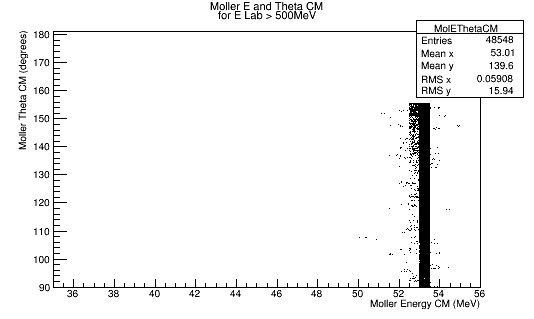
Using the histogram for Theta in the CM frame, we can determine the relative number of events that occur at a given angle. This information will be used to keep the relative number of particles having the same Theta angle, but multiple Psi angles to evenly cover the detector area
Run for Necessary Amount to match Cross Section
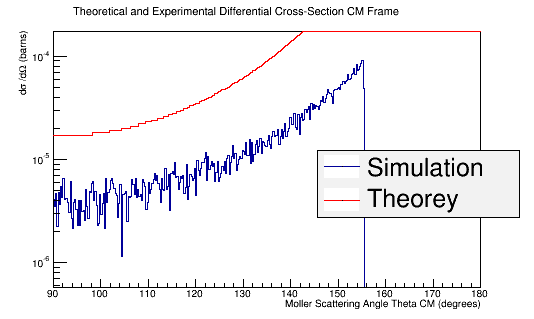
Using the above plot for the target material, we can find the relative amount that each Theta angle should observe for this process which gives a known Moller differential cross section.
| Theta (degrees) | Number of events |
|---|---|
| 90 | 5 |
| 100 | 5 |
| 110 | 6 |
| 120 | 8 |
| 130 | 12 |
| 135 | 20 |
| 140 | 28 |
| 142 | 30 |
| 144 | 40 |
| 146 | 45 |
| 148 | 55 |
| 150 | 70 |
| 152 | 80 |
| 154 | 100 |
We can set up conditional statements to check what range the Theta angle falls in, then by dividing
we should find the change in phi needed to give an evenly distributed distribution around the xy plane for a given Theta angle.