need to insert moller shielding into card after moller LUND file is created. (see clas12/beamline)
Simulating the Moller scattering background for EG12
GEANT4 Simulation of Moller Events
Simulation Setup
Determine the Moller background using an LH2 target to check the physics in GEANT4
Distributions For LH2
Comparing experimental vs. theoretical for Møller differential cross section 11GeV
Converting the number of scattered electrons per scattering angle theta to a differential cross-section in barns.
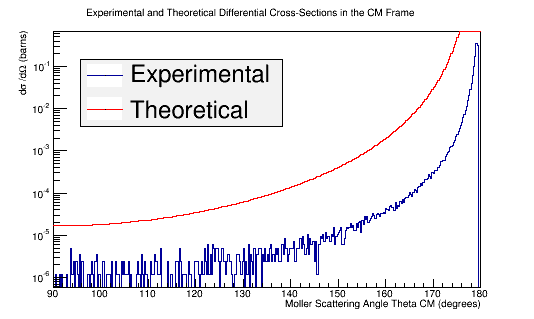
Figure 5c: The experimental and theoretical Moller electron differential cross-section for an incident 11 GeV(Lab) electron in the Center of Mass frame of reference.
Change to a NH3 Target
Replacing the LH2 target with an NH3 target
NH3 Momentum Distribution in the Lab Frame
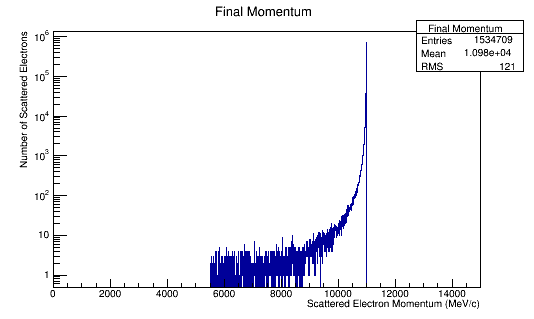
Figure 6a: The scattered electron momentum distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
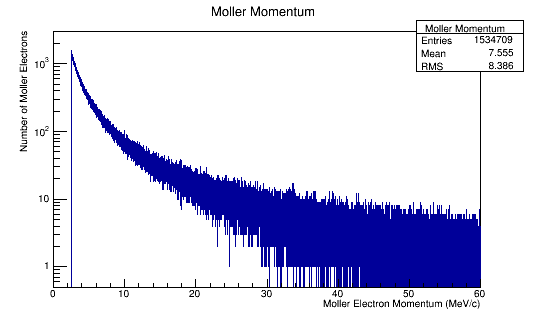
Figure 6b: The Moller electron momentum distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
Increasing the number of incident electrons, Moller Momentum now appears as:
NH3 Momentum Distribution in the Center of Mass Frame
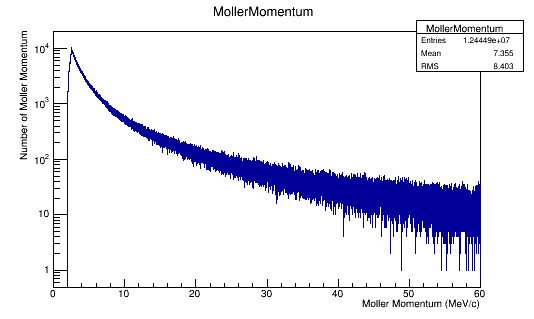
Figure 6c: The Moller electron momentum distribution for 4E8 incident 11 GeV electrons in the Lab frame of reference.
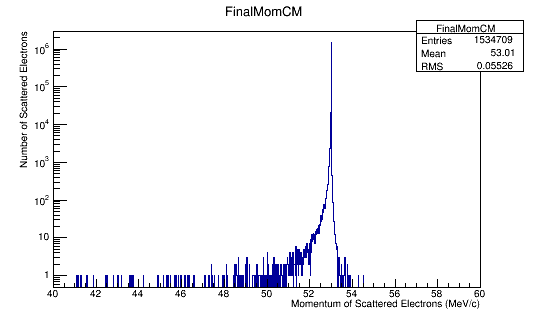
Figure 6d: The scattered electron momentum distribution for 4E7 incident 11 GeV(Lab) electrons in the Center of Mass frame of reference.
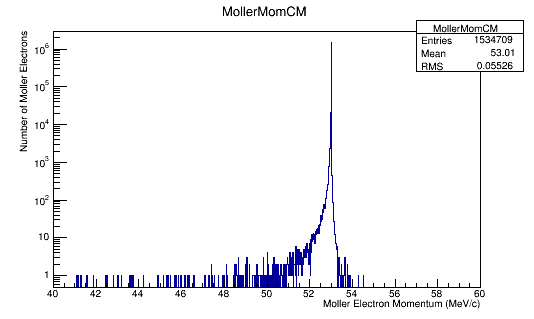
Figure 6e: The Moller electron momentum distribution for 4E7 incident 11 GeV(Lab) electrons in the Center of mass frame of reference.
NH3 Angular Distribution in the Lab Frame
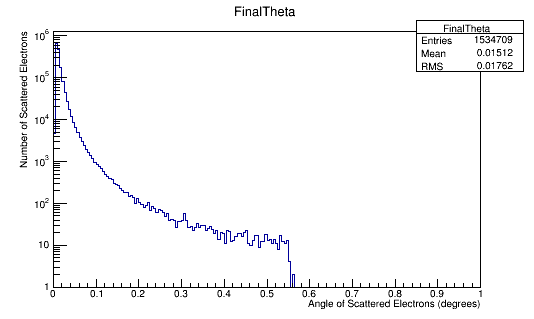
Figure 6f: The Moller electron scattering angle thetea distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.

Figure 6g: The Moller electron scattering angle theta distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
NH3 Angular Distribution in the Center of Mass Frame
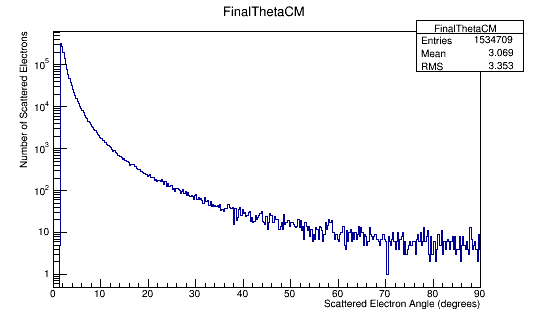
Figure 6h: The Scattered electron scattering angle theta distribution for 4E7 incident 11 GeV(Lab) electrons in the Center of Mass frame of reference.
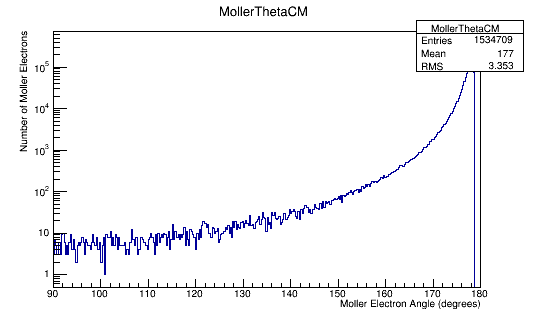
Figure 6i: The Moller electron scattering angle theta distribution for 4E7 incident 11 GeV(Lab) electrons in the Center of Mass frame of reference.
LH2 Vs. NH3
Plotting the Momentum and Scattering angle Theta in the Lab and Center of Mass frame of reference for LH2 and NH3 targets.
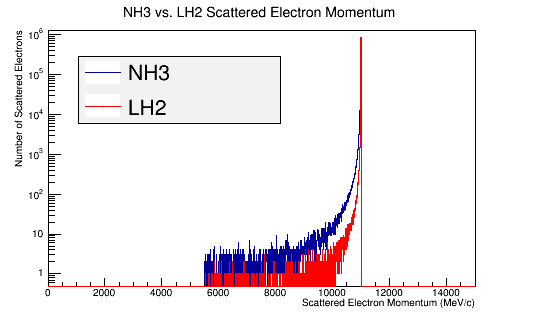
Figure 7a: The scattered electron momentum distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
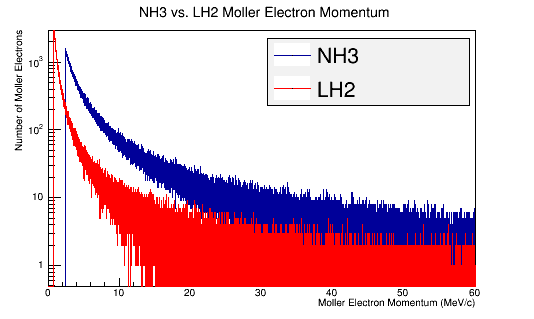
Figure 7b: The Moller electron momentum distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
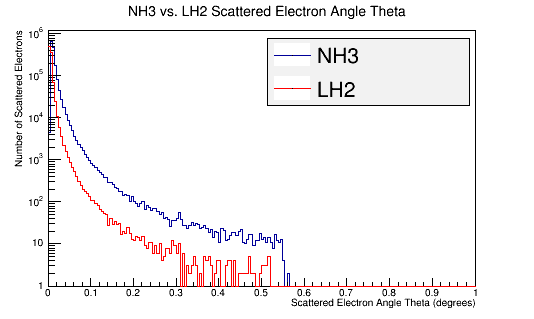
Figure 7c: The Scattered electron scattering angle theta distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
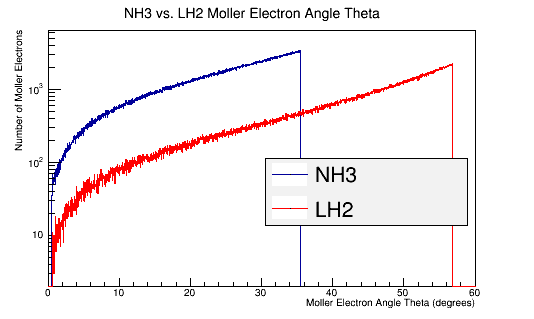
Figure 7d: The Moller electron scattering angle theta distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
Figure out the offset
Rerunning the GEANT simulation for a target of solo atoms of Carbon 12
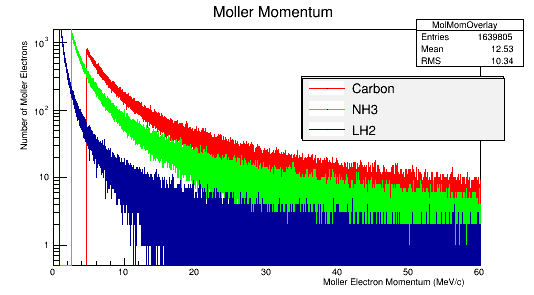
Figure 8a: The scattered electron momentum distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
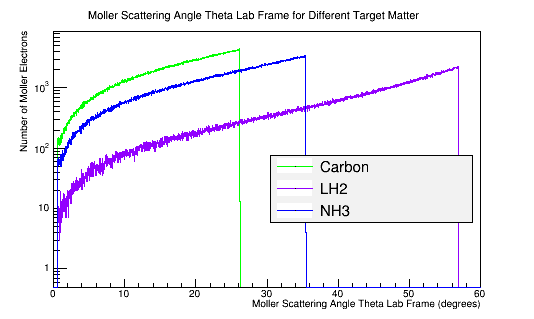
Figure 8b: The Moller electron momentum distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
These graphs show an offset based upon the density of the target material.
Density of target material
C=2.26 g/cm3
NH3=.86g/cm3
LH2=.07g/cm3
[math]\Longrightarrow[/math]The greater the density, the smaller the solid angle into which the Moller electron will scatter.
Density, atomic mass, and electron number effects
Temporarily changing the density of LH2 to be .86g/cm3, the density of NH3, and altering the atomic mass and electron number, we find
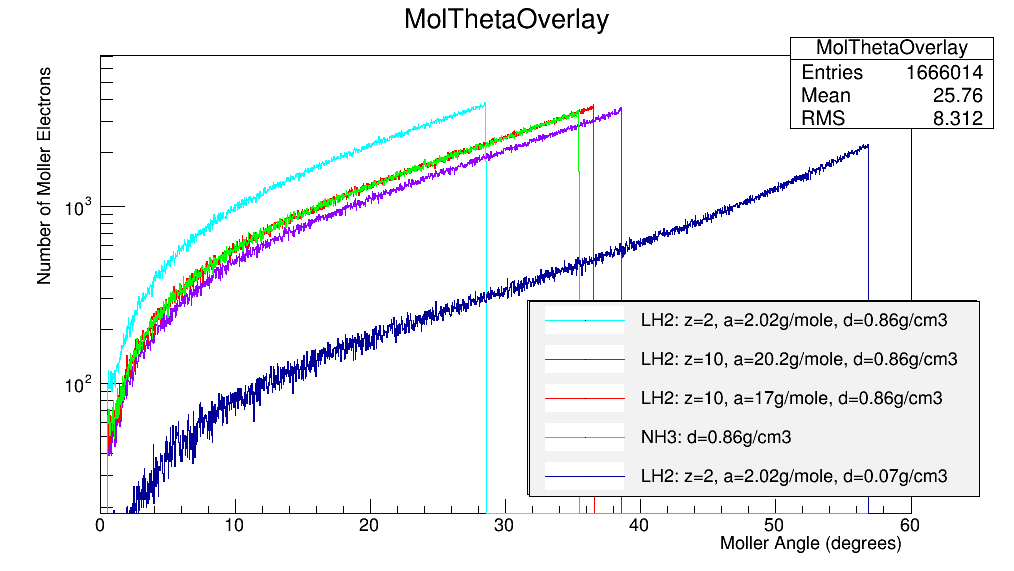
Figure 8c: The Moller electron scattering angle theta distribution for 4E7 incident 11 GeV electrons in the Lab frame of reference.
Differential Cross-Section Offset
Comparing this to the theoretical differential cross section:
As shown above , we find that the differential cross section scale is [math]\frac{d\sigma}{d\Omega}\approx 16.2\times 10^{-2}mb=16.2\mu b[/math]
Converting the number of electrons to barns,
[math]L=\frac{i_{scattered}}{\sigma} \approx i_{scattered}\times \rho_{target}\times l_{target}[/math]
where ρtarget is the density of the target material, ltarget is the length of the target, and iscattered is the number of incident particles scattered.
For LH2:
[math]\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1m^3}{(100 cm)^3} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^{2}}{barn} =2.10\times 10^{-2} barns[/math]
[math]\frac{1}{\rho_{target}\times l_{target} \times 4\times 10^7}=1.19\times 10^{-6} barns[/math]
For Carbon:
[math]\rho_{target}\times l_{target}=\frac{2.26 g}{1 cm^3}\times \frac{1 mole}{12.0107 g} \times \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^{2}}{barn} =1.13\times 10^{-1} barns[/math]
[math]\frac{1}{\rho_{target}\times l_{target} \times 4\times 10^7}=2.21\times 10^{-7} barns[/math]
For Ammonia:
[math]\rho_{target}\times l_{target}=\frac{.8 g}{1 cm^3}\times \frac{1 mole}{17 g} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^2}{barn} =2.82\times 10^{-2} barns[/math]
[math]\frac{1}{\rho_{target}\times l_{target} \times 4\times 10^7}=8.87\times 10^{-7} barns[/math]
Combing plots in Root:
new TBrowser();
TH1F *LH2=new TH1F("LH2","LH2",360,90,180);
LH2->Add(MollerThetaCM,1.19e-6);
LH2->Draw();
TH1F *C12=new TH1F("C12","C12",360,90,180);
C12->Add(MollerThetaCM,2.21e-7);
C12->Draw();
TH1F *NH3=new TH1F("NH3","NH3",360,90,180);
NH3->Add(MollerThetaCM,8.87e-7);
NH3->Draw();
LH2->Draw("same");
C12->Draw("same");
Theory->Draw("same");
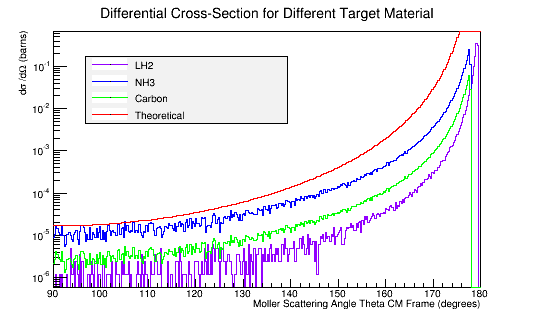
Figure 8c: The Moller electron differential cross-section for 4E7 incident 11 GeV electrons in the Center of Mass frame of reference.
Reconstruction
Moller Track Reconstruction in eg12
Papers used
[1]Farrukh Azfar's Derivation of Moller Scattering
- File:FarrukAzfarMollerScatter.pdf
A polarized target for the CLAS detector
- File:PHY02-33.pdf
An investigation of the spin structure of the proton in deep inelastic scattering of polarized muons on polarized protons
- File:1819.pdf
QED Radiative Corrections to Low-Energy Moller and Bhabha Scattering
http://arxiv.org/abs/1602.07609
EG12

















