PbBi BeamPipeHeatin 2015
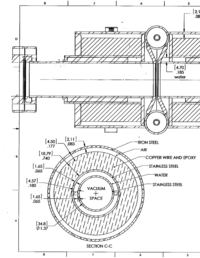
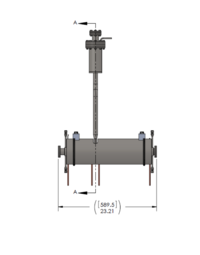
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm.
| Element | dimension |
| Inner beam pipe radius | 1.74 cm |
| Inner beam pipe thickness | 0.165 cm |
| water jacket thickness | 0.457 cm |
| outer beam pipe radius | 2.362 cm |
| outer beam pipe thickness | 0.165 cm |
| Solenoid inner radius | 2.527 cm |
| Solenoid outer radius | 4.406 cm |
Max power deposited in beam pipe from uniform beam heating
If you assume a 1mA beam then the beam power incident on the target is
Beam Power = E(MeV) I ( A) = 10 MeV 1000 mA = 10 kW
If the beam does not interact with the target and all the beam power is distributed uniformly along a 100 cm long beam pipe with a diameter of 3.48 cm then the power deposited per area would be
A simulation predicts that about 8 out of 20 electrons will interact with the target and intercept a 34.8 mm diameter beam pipe surrounding the target.
BUT the beam does not intersect the pipe uniformly and instead can have a hot spot.
Heating along the Z-axis
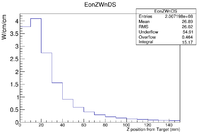
GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit
 |

|
According to the above figure, GEANT4 predicts a total of MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target. The peak energy deposition is 0.3 MeV/e
If this energy were uniformly distributed along the 5 mm thick beam pipe having a diameter of 3.48 cm then I would see
if you assume a 1 mA beam of electrons then this becomes
I converted the above histogram to deposited power by 1000 mA, divide by the number of incident electrons, divide by the circumference of the beam pipe, convert the number of electrons to Coulombs, and use a unit conversion from MeV to W-s per MeV.
If you use the above factors to weight the histogram, then the figure below shows that GEANT4 predicts a power deposition density of , 1 cm downstream of the target. Back scattered electrons appear to create the hottest spot of about 1cm upstream of the target.
 |

|
| Power Deposition Zoomed in and 902 mm offset applied | Power deposition over the 1 m long beam pipe |
BeamPipeHeating_4mmthick_PbBi_PositronTarget
NiowaveTargetHeatingResult_2015
Unit conversion
The energy deposited by photon, electrons, and positrons is predicted by GEANT4 and recorded in energy units of keV per incident electron on the PbBi target. To convert this deposited energy to a power you need to assume a beam current. Assuming 1 beam current of 1 mA, the conversion is given easily as
Results Table
| Beam Pipe Diameter (mm) | Hot Spot () |
| 34.8 | 0.35 |
| 47.5 | 0.24 |
| 60.2 | 0.20 |
| 72.9 | 0.16 |
| 97.4 | 0.12 |