Verification of Relativistic Components
Jump to navigation
Jump to search
Verifying that the kinematics are valid, the Moller momentum from GEANT simulations are extracted using
awk '{print $16, $17, $18}' MollerScattering_NH3_Large.dat > Just_Mol_Mom.dat
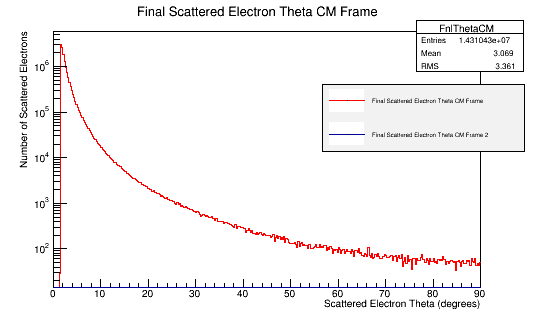
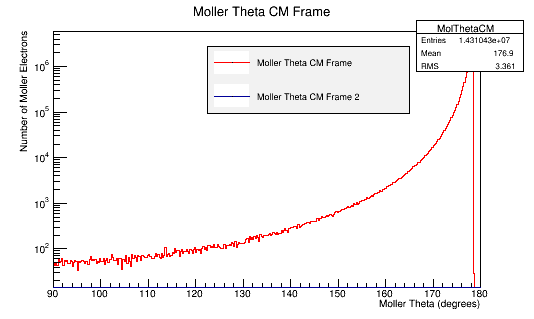
Then using the kinematics equations displayed above, used to reverse calculate the scattered electron's momentum and angles. The root histograms of an incoming 11GeV electron (in blue) are overlaid with the relativistic calculations starting with the Moller electron (Reverse Moller in red) and show good agreement.
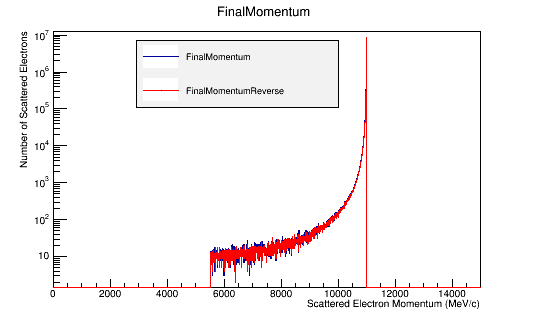
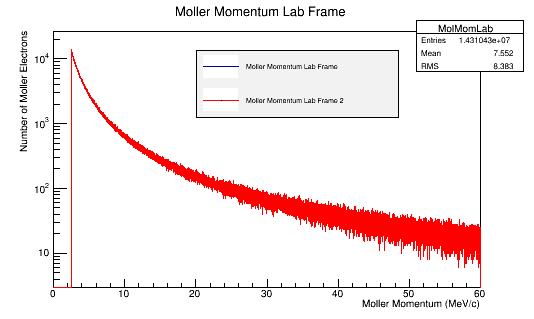
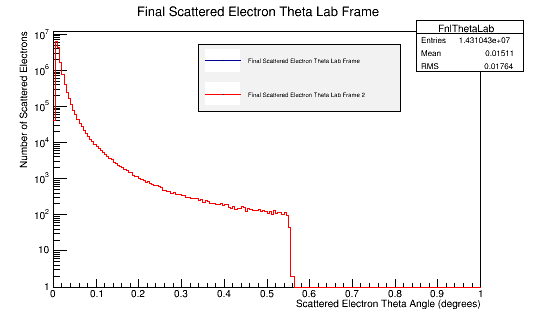
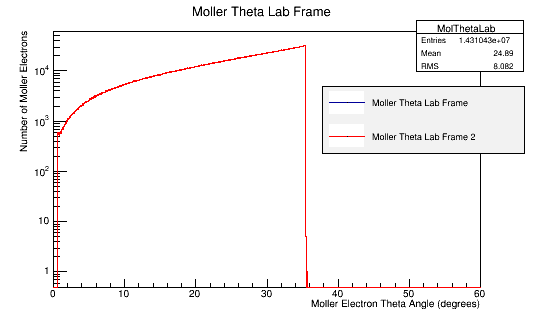
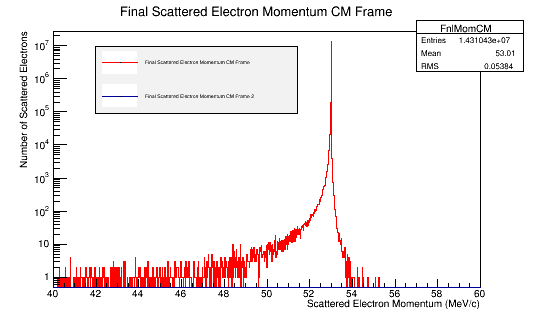
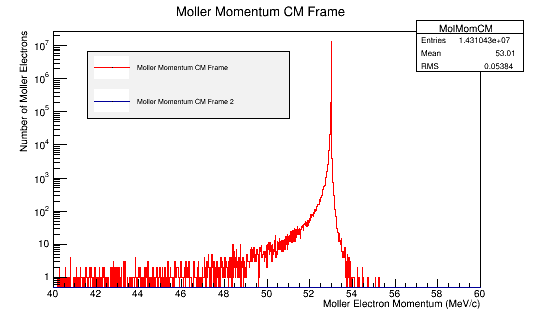
The differences in these plots come from the way the CM frame momentum is calculated.
- For the process starting with the Moller electron's momentum and working backwards to find the scattered electron:
- This only gives z component momentum.
- For the process using the scattered electron and Moller electron's momentum to find the CM frame:
- This allows momentum in all 3 cartesian coordinates.