DV RunGroupC Moller

Simulating the Moller scattering background for EG1

Step 1

Determine the Moller background using an LH2 target to check the physics in GEANT4

Incident electron energy varies from 1-11 GeV.

LH2 target is a cylinder with a 1.5 cm diameter and 1 cm thickness.

  (Following dimensions listed on page 8 of File:PHY02-33.pdf)

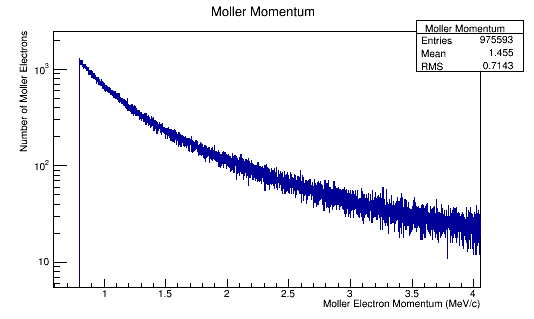
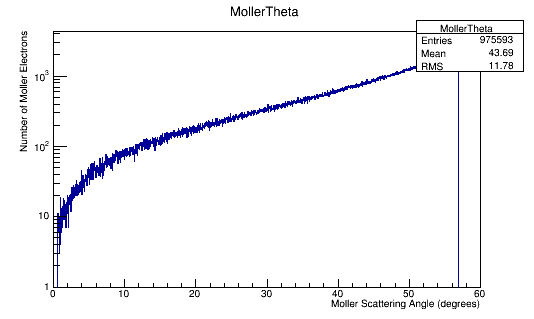
Numbers Moller electrons per incident electron.

  While 2nd and 3rd generations are created, only 2 2nd generation daughter particles are created for 1E6 incident particles.  All knock on electrons are not counted.

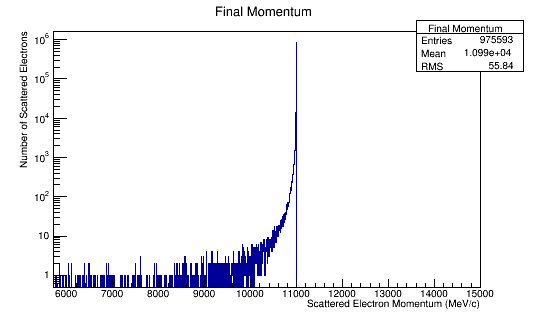
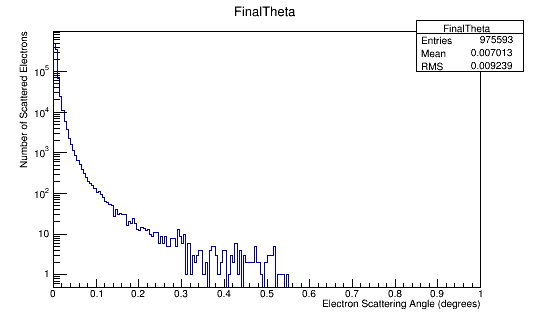
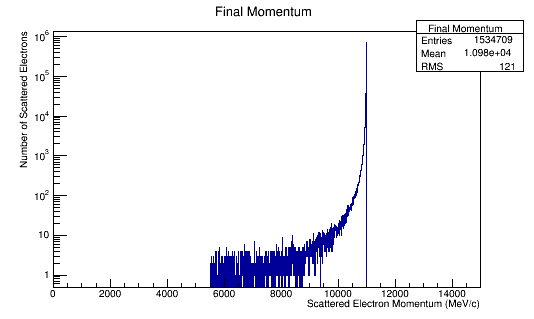
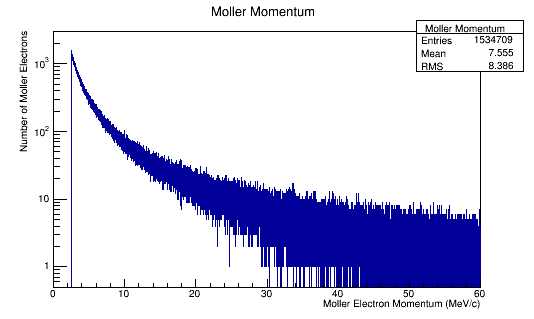
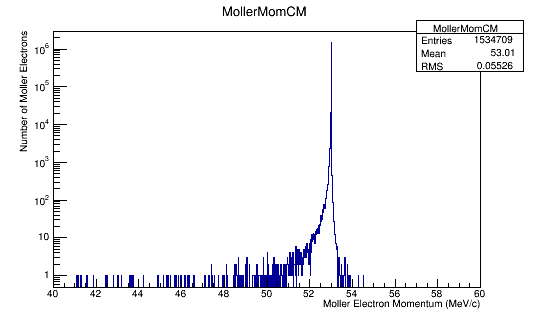
Momentum distributions in the Lab Frame.

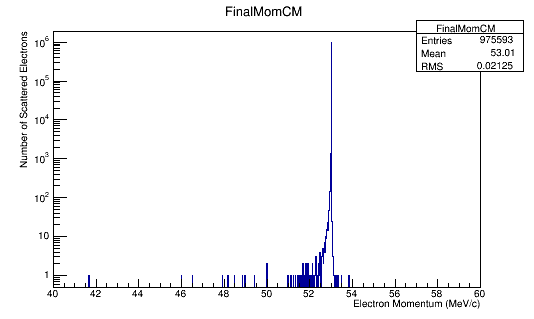
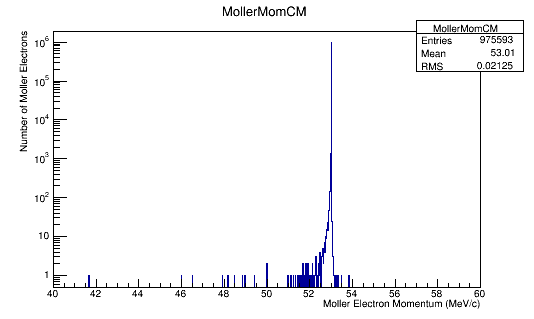
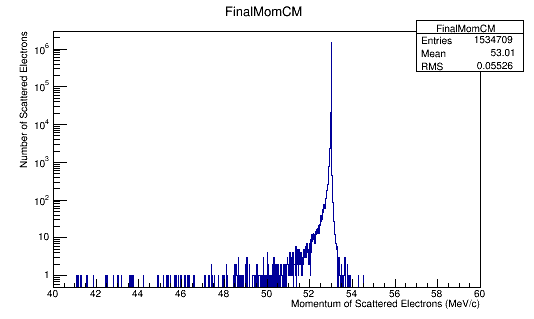
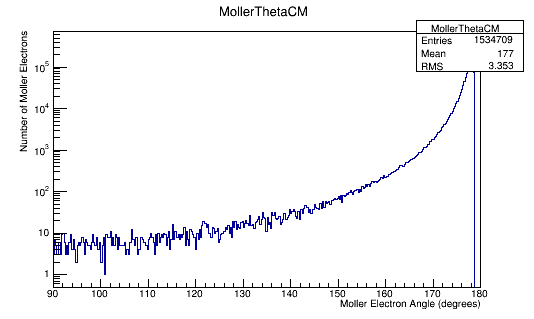
Momentum distributions in the Center of Mass Frame.

Estimated Momentum Distribution

In the collision of two particles of mass m_1 and m_2, the total energy in the center of mass frame can be written

[math]E_{cm}=[(E_{1lab}+E_{2lab})^2-(\vec{p_{1lab}}+p_{2lab})^2]^{1/2}[/math]

[math]E_{cm}=[m_1^2+m_2^2+2E_1E_2(1-\beta_1\beta_2cos\theta)]^{1/2}[/math] where θ is the angle between the particles.

In the frame where one particle (m₂) is at rest

[math]E_{cm}=(m_1^2+m_2^2+2E_{1_{initial} lab}m_2)^{1/2}[/math]

where [math]E_{1_{initial} lab}=KE_{1_{initial} lab}+m_1[/math] in MeV

The velocity of the center of mass in the lab frame is

[math]\beta_{cm}=\frac{p_{1_{initial}lab}}{(E_{1_{initial} lab}+m_2)}[/math]

[math]\gamma_{cm}\frac{(E_{1_{initial} lab}+m_2)}{E_{cm}}[/math]

This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions

[math]p_{cm}=\frac{p_{1_{initial}lab}m_2}{E_{cm}}[/math]

For an incoming electron with momentum of 11GeV, we should find the momentum in the center of mass to be around 53 MeV which is confirmed in the the data/plots.

KEi	Pxi	Pyi	Pzi	xi	yi	z1	KEf	Pxf	Pyf	Pzf	xf	yf	zf	KEm	Pxm	Pym	Pzm	xm	ym	zm
11000	0	0	11000.5	0	0	-510	10999.1	0.433025	-0.858867	10999.6	0	0	-509.276	0.905324	-0.433025	0.858867	0.905366	0	0	-509.276

Changing the code for the total Energy to [math]E=(p_1^2+m_1^2)^{1/2}[/math] in the lab frame gives

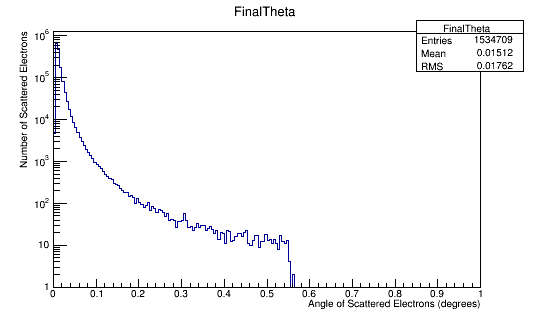
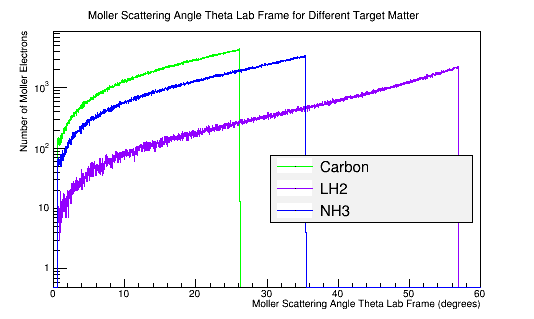
Angular Distribution in the Lab Frame

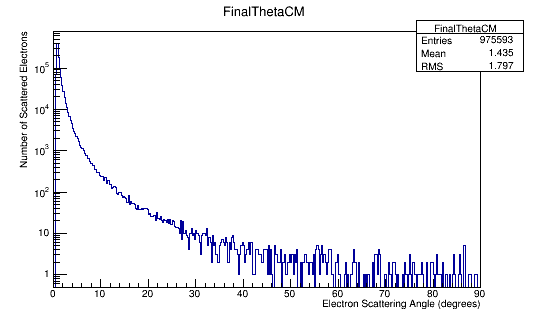
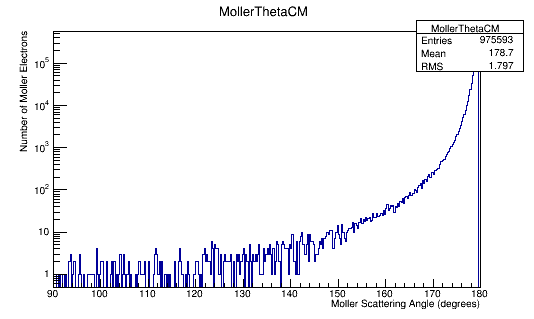
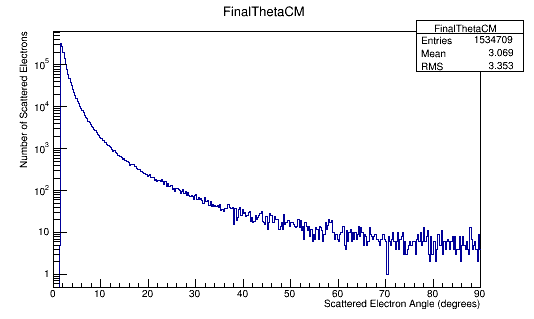
Angular Distribution in the Center of Mass Frame

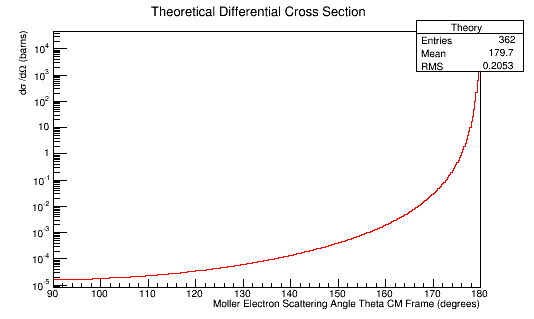
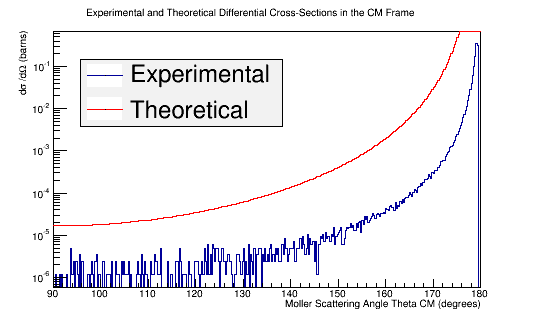
Comparing experimental vs. theoretical for Møller differential cross section 11GeV

Using the equation from [1]

[math]\frac{d\sigma}{d\Omega}=\frac{ e^4 }{8E^2}\left \{\frac{1+cos^4\frac{\theta}{2}}{sin^4\frac{\theta}{2}}+\frac{1+sin^4\frac{\theta}{2}}{cos^4\frac{\theta}{2}}+\frac{2}{sin^2\frac{\theta}{2}cos^2\frac{\theta}{2}} \right \}[/math]

where [math]\alpha=\frac{e^2}{\hbar c}\quad with\quad \hbar = c =1[/math]

This can be simplified to the form

[math]\frac{d\sigma}{d\Omega}=\frac{ \alpha^2 }{4E^2}\frac{ (3+cos^2\theta)^2}{sin^4\theta}[/math]

Plugging in the values expected for a scattering electron:

[math]\alpha ^2=5.3279\times 10^{-5}[/math]

[math]E\approx 53 MeV[/math]

Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around

[math]\frac{5.3279\times 10^{-5}}{4\times 2.809\times 10^{15}eV^2}=4.74\times 10^{-21} eV^{-2}=\frac{4.74\times 10^{-21}}{1eV^2}\times \frac{1\times 10^{18} }{1\times 10^{18}}=\frac{.0047}{GeV^2}[/math]

Using the conversion of

[math]\frac{1}{1GeV^2}=.3894 mb[/math]

We find that the differential cross section scale is [math]\frac{d\sigma}{d\Omega}\approx 2\times 10^{-3}mb=2\mu b[/math]

Converting the number of electrons to barns,

[math]L=\frac{i_{scattered}}{\sigma} \approx i_{scattered}\times \rho_{target}\times l_{target}[/math]

where ρ_target is the density of the target material, l_target is the length of the target, and i_scattered is the number of incident particles scattered.

[math]L=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1cm}{100 cm} \times \frac{1 m}{ } \times \frac{10^{-23} m^2}{barn} =2.10\times 10^{-2} barns[/math]

[math]\frac{1}{L \times 4\times 10^7}=1.19\times 10^{-6} barns[/math]

Combining these plots, and rescaling the Final Theta in the Center of Mass for micro-barns, we find

Step 2

Replace the LH2 target with an NH3 target and compare with LH2 target.

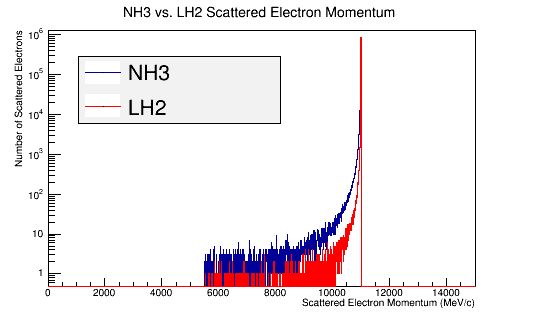
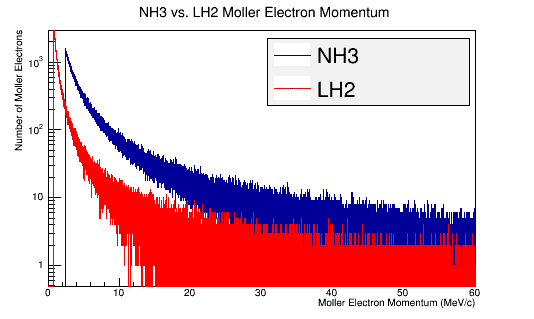
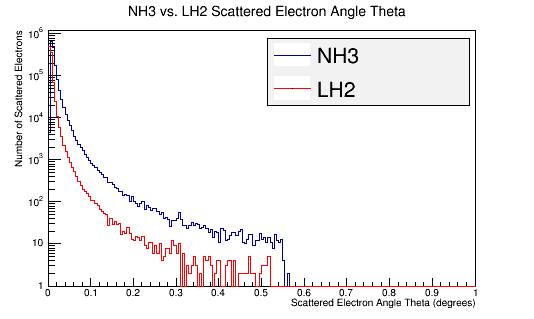
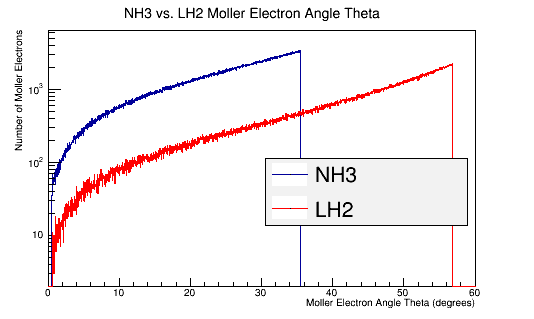
LH2 Vs. NH3

[math]L=\frac{870 kg}{1 m^3}\times \frac{1 mole}{17.03 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1cm}{100 cm} \times \frac{1 m}{ } \times \frac{10^{-23} m^2}{barn} =2.10\times 10^{-2} barns[/math]

Figure out the offeset

Rerunning the GEANT simulation for a target of solo atoms of Carbon 12, with 4^{10} incident 11GeV electrons

Step 3

Determine impact of Solenoid magnet on Moller events

Papers used

[1]Farrukh Azfar's Derivation of Moller Scattering

File:FarrukAzfarMollerScatter.pdf

A polarized target for the CLAS detector

File:PHY02-33.pdf

An investigation of the spin structure of the proton in deep inelastic scattering of polarized muons on polarized protons

File:1819.pdf

EG12