Kiwi Dipole Mappings

From New IAC Wiki
Jump to navigation Jump to search

Kiwi Dipole Documents

Cad drawing of kiwi dipole:

File:Hrrl pos wiki dipole 1.pdf File:Hrrl pos wiki dipole 2.pdf File:Hrrl pos wiki dipole 3.pdf File:Hrrl pos wiki dipole 4.pdf File:Hrrl pos wiki dipole 5.pdf

Bending Radius of the kiwi dipole is 318.5 mm, and it bends beam by 45 degree.

The path of the beam in the dipole then [math] S = \rho \times \theta = 318.5 \times \pi/4 = 318.5 \times 3.14159265 / 4 = 250.149315~ mm[/math]

1st Mapping

File:Kiwi Dipole Magnet Mappings.pdf

Tag Number: 079220

Bending magnet that was to be used with LCS (compact magnets) The horizontal and vertical tranlator have a range for 150 mm i.e. 15 cm.

Power on I = 20.4 A

x (mm) y (mm) B (kG)
127 0 [math] -6.7 \times 10^{-2} [/math]
127 10 -0.106
127 20 -0.169
127 30 -0.2729
127 40 -0.448
127 50 -0.728
127 60 -0.97
127 70 -1.025
127 80 -1.029
127 90 -1.03
127 100 -1.029
127 110 -1.028
127 120 -1.028
127 130 -1.028
127 140 -1.028
127 150 -1.028
y = 150 mm is roughly center of the bend.
127 150 -1.028
127 140 -1.031
127 130 -1.0342
127 120 -1.036
127 110 -1.036
127 100 -1.036
127 90 -1.036
127 80 -1.0355
127 70 -1.03
127 60 -0.977
127 50 -0.7354
127 40 -0.4527
127 30 -0.275
127 20 -0.17
127 10 -0.1066
127 0 -0.0673
Again
x (mm) y (mm) B (kG)
127 0 [math] -0.0672 [/math]
127 10 -0.1062
127 20 -0.1699
127 30 -0.2738
127 40 -0.449
127 50 -0.7283 edge of poles 100 px
127 60 -0.9712
127 70 -1.0253
127 80 -1.03
127 90 -1.03
127 100 -1.0298
127 110 -1.028
127 120 -1.0285
127 130 -1.0286
127 140 -1.0282
127 150 -1.0278 



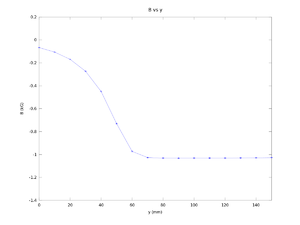
     y (mm)      B (kG)   error B (kG)
    0.00000    -0.06717     0.00015
   10.00000    -0.10627     0.00031
   20.00000    -0.16963     0.00055
   30.00000    -0.27390     0.00105
   40.00000    -0.44990     0.00248
   50.00000    -0.73057     0.00419
   60.00000    -0.97273     0.00374
   70.00000    -1.02677     0.00280
   80.00000    -1.03150     0.00350
   90.00000    -1.03200     0.00346
  100.00000    -1.03160     0.00383
  110.00000    -1.03067     0.00462
  120.00000    -1.03083     0.00448
  130.00000    -1.03027     0.00342
  140.00000    -1.02907     0.00168
  150.00000    -1.02793     0.00012

Mapping Figure 079220 X127 I204A.png

X at 127, Y at 150

x (mm) y (mm) I B (kG)
127 150 20.1 -1.0279
127 150 30.1 -1.53
127 150 25.1 -1.2916
127 150 20.1 -1.0359
127 150 15 -0.781
127 150 10 -0.534
127 150 5 -0.277
127 150 0 -0.017
Again
127 150 0 -0.01726
127 150 5 -0.266
127 150 10 -0.518
127 150 15 -0.7713
127 150 20 -1.02
127 150 25 -1.272
127 150 30 -1.52 



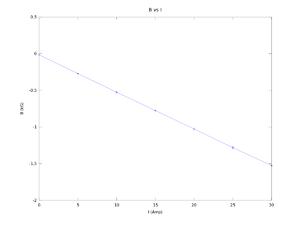
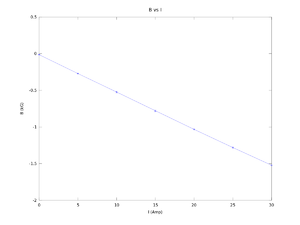
  I (Amps)    B (kG)    error B (kG)
   0.00000   -0.01713    0.00018
   5.00000   -0.27150    0.00778
  10.00000   -0.52600    0.01131
  15.00000   -0.77615    0.00686
  20.00000   -1.02795    0.01124
  25.00000   -1.28180    0.01386
  30.00000   -1.52500    0.00707

Mapping Figure 079220 X127 Y150.png

Vertical Scan

Power on I = 20 A

Gap width [math] \approx [/math]5cm.

x (mm) y (mm) B (kG)
135 (lower edge) 150 -1.0369
132 150 -1.0379
129 150 -1.0382
126 150 -1.0384
123 150 -1.0385
120 150 -1.0386
118 150 -1.0387
116 150 -1.0388
114 150 -1.039 


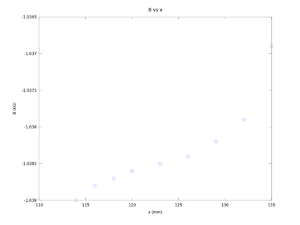
   x (mm)      y(mm)       B(kG)
  135.0000   150.0000    -1.0369
  132.0000   150.0000    -1.0379
  129.0000   150.0000    -1.0382
  126.0000   150.0000    -1.0384
  123.0000   150.0000    -1.0385
  120.0000   150.0000    -1.0386
  118.0000   150.0000    -1.0387
  116.0000   150.0000    -1.0388
  114.0000   150.0000    -1.0390

Mapping Figure 079220 X127 I120.png

Horizontal Scan

go for X = 124.5, y = 150 (dipole center), I = 20 A.


x (mm) y (mm) I (A) B (kG)
124.5 150 20 -1.0388
124.5 140 20 -1.04
124.5 130 20 -1.04
124.5 120 20 -1.0409
124.5 110 20 -1.041
124.5 100 20 -1.0411
124.5 90 20 -1.041
124.5 80 20 -1.0408
124.5 70 20 -1.355 This data is problematic.
124.5 60 20 -0.9799
124.5 50 20 -0.74
124.5 40 20 -0.457
124.5 30 20 -0.2776
124.5 20 20 -0.1718
124.5 0 20 -0.0684


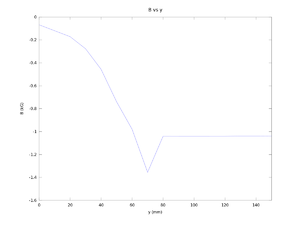
Figure according to the data above. There is problem when y = 70 mm. Mapping Figure 079220 X1245 I20 original.png 

   x (mm)      y  (mm)       I (A)      B  (kG)   
  124.50000   150.00000    20.00000    -1.03880
  124.50000   140.00000    20.00000    -1.04000
  124.50000   130.00000    20.00000    -1.04000
  124.50000   120.00000    20.00000    -1.04090
  124.50000   110.00000    20.00000    -1.04100
  124.50000   100.00000    20.00000    -1.04110
  124.50000    90.00000    20.00000    -1.04100
  124.50000    80.00000    20.00000    -1.04080
  124.50000    70.00000    20.00000    -1.03550
  124.50000    60.00000    20.00000    -0.97990
  124.50000    50.00000    20.00000    -0.74000
  124.50000    40.00000    20.00000    -0.45700
  124.50000    30.00000    20.00000    -0.27760
  124.50000    20.00000    20.00000    -0.17180
  124.50000     0.00000    20.00000    -0.06840

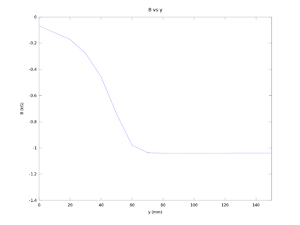
Figure according to the data above. The problem when y = 70 mm is changed to -1.0355 Mapping Figure 079220 X1245 I20 amended.png


Power on X = 124.5, Y = 150

x (mm) y (mm) I (A) B (kG)
124.5 150 0 -0.0123
124.5 150 5 -0.2676
124.5 150 10 -0.516
124.5 150 15 -0.771
124.5 150 20 -1.028
124.5 150 25 -1.2735
124.5 150 30 -1.5217
124.5 150 30 -1.5218
124.5 150 25 -1.287
124.5 150 20 -1.037
124.5 150 15 -0.7855
124.5 150 10 -0.5313
124.5 150 5 -0.2747
124.5 150 0 -0.0164 


    I (A)      B(kG)    error B(kG) 
  30.00000   -1.52175    0.00007
  25.00000   -1.28025    0.00955
  20.00000   -1.03250    0.00636
  15.00000   -0.77825    0.01025
  10.00000   -0.52365    0.01082
   5.00000   -0.27115    0.00502
   0.00000   -0.01435    0.00290


Mapping Figure 079220 X1245 Y150 amended.png

Tag Number: 42125

x (mm) y (mm) I (A) B (kG)
0 0 Power off [math]-3 \times 10^{-4}[/math]
0 0 20 [math]-6 \times 10^{-3}[/math]
111.75 0 20 [math] 0.0405[/math]



x (mm) y (mm) I (A) B (kG)
111.75 10 20 0.0637
111.75 20 20 0.102
111.75 30 20 0.1675
111.75 40 20 0.2774
111.75 50 20 0.4654
111.75 60 20 0.756
111.75 70 20 0.9898
111.75 80 20 1.0312
111.75 90 20 1.0358
111.75 100 20 1.0362
111.75 110 20 1.0363
111.75 120 20 1.0363
111.75 130 20 1.0362
111.75 140 20 1.036
111.75 150 20 1.036
111.75 0 20 0.0402
111.75 10 20 0.0635
111.75 20 20 0.1022
111.75 30 20 0.1674
111.75 40 20 0.2773
111.75 50 20 0.4652
111.75 60 20 0.755
111.75 70 20 0.9828
111.75 80 20 1.0312
111.75 90 20 1.0358
111.75 100 20 1.0362
111.75 110 20 1.0362
111.75 120 20 1.03625
111.75 130 20 1.0362
111.75 140 20 1.036
111.75 150 20 1.036



x (mm) y (mm) I (A) B (kG)
111.75 150 0 0.0076
111.75 150 5 0.263
111.75 150 10 0.52
111.75 150 15 0.7754
111.75 150 20 1.0313
111.75 150 25 1.2869
111.75 150 30 1.5389
111.75 150 30 1.5389
111.75 150 25 1.3
111.75 150 20 1.0484
111.75 150 15 0.7945
111.75 150 10 0.534
111.75 150 5 0.276
111.75 150 0 0.01386



x (mm) y (mm) I (A) B (kG)
123.25 150 20 1.0339
120.25.25 150 20 1.0338
117.25 150 20 1.034
114.25 150 20 1.034
111.25 150 20 1.0342
111.25 150 20 1.0343
108.25 150 20 1.0342
105.25 150 20 1.0343
102.25 150 20 1.0344
99.25 150 20 1.03435



x (mm) y (mm) I (A) B (kG)
111.25 150 20 1.0339
111.25 0 20 0.04
111.25 10 20 0.0633
111.25 20 20 0.102
111.25 30 20 0.1671
111.25 40 20 0.2767
111.25 50 20 0.4643
111.25 60 20 0.7544
111.25 70 20 0.9818
111.25 80 20 1.0295
111.25 90 20 1.034
111.25 100 20 1.0344
111.25 110 20 1.0345
111.25 120 20 1.0345
111.25 130 20 1.0345
111.25 140 20 4.0343
111.25 150 20 10.342
111.25 0 20 0.04
111.25 10 20 0.0632
111.25 20 20 0.1018
111.25 30 20 0.1669
111.25 40 20 0.2767
111.25 50 20 0.4639
111.25 60 20 0.754
111.25 70 20 0.9816
111.25 80 20 1.0294
111.25 90 20 1.034
111.25 100 20 1.0344
111.25 110 20 1.0344
111.25 120 20 1.0344
111.25 130 20 1.0343
111.25 140 20 4.0342
111.25 150 20 10.342



x (mm) y (mm) I (A) B (kG)
111.25 43 mm 0 [math]3.6 \times 10^{-3}[/math]
111.25 43 mm 5 0.0822
111.25 43 mm 10 0.1615
111.25 43 mm 15 0.242
111.25 43 mm 20 0.3227
111.25 43 mm 25 0.4014
111.25 43 mm 30 0.4793
111.25 43 mm 0 [math]2.8 \times 10^{-3}[/math]
111.25 43 mm 5 0.08
111.25 43 mm 10 0.1613
111.25 43 mm 15 0.242
111.25 43 mm 20 0.3215
111.25 43 mm 25 0.4
111.25 43 mm 30 0.4783


2nd Mapping

Bending radius of dipole is 319 mm. The bending radius in measurement is r = 280 mm.

Mapping of the dipole was divided into 3 parts according to the path of the ideal particle. This trajectory of particle with ideal energy should go through a fringe field (approximately straight line) and dipole field (rotation of near 45 degree with dipole bending radius of 319 mm), and another fringe field (approximately straight line). We called them A2 (entering fringe field), Rotation and A1 (Exiting fringe field).

A2

       I= - 6.5 A	I= - 15.25 A	I= - 24 A	I= - 33 A		
Z(mm) 	B (G)	        B (G)	         B (G)	         B (G)		
81.50	-55.2500	-128.3700	200.6800	-273.6085		
82.50	-52.6000	-122.1600	-191.0000	-260.3194		
83.50	-50.0700	-116.2700	-181.7600	-247.6903		
84.50	-47.6700	-110.6800	-173.0100	-235.7135		
85.50	-45.4000	-105.3700	-164.6920			
87.50	-41.1800	-95.5400	-149.2710	-203.2767		
89.50	-37.3800	-86.6600	-135.3760	-184.2830		
91.50	-33.9600	-78.6600	-122.8530	-167.1615		
93.50	-30.8600	-71.4600	-111.5640	-151.7285		
95.50	-28.0800	-64.9700	-101.3870	-137.8432		
98.00	-25.1200	-57.7600	-90.1060	-122.3860		
100.00	-22.8900	-52.6200	-82.0500	-111.3860		
103.00	-19.9800	-45.8400	-71.4230	-96.9286		
105.00	-18.2600	-41.8600	-65.1930	-88.3740		
110.00	-14.6600	-33.5200	-52.1380	-70.5650		
115.00	-11.8500	-27.1700	-41.9210			
120.00	-9.6500 	-22.0600	-34.0260	-45.8887		
130.00	-6.5400 	-14.8400	-22.9290	-30.7577		
140.00	-4.5600	        -10.2500	-15.7670	-21.0309		
150.00	-3.2600	        -7.2600	        -11.0980	-14.7070


A1

       I= - 6.505 A	I= - 15.25 A		I= - 24 A	        I= - 33 A
Z(mm) 	B (G)	         B (G)		        Z(mm) 	B (G)	        B (G)
137.50	-69.4460	-160.7070		137.50	-252.3900	-342.9800
136.50	-66.4320	-153.7000		136.50	-241.2700	-328.0530
135.50	-63.5170	-146.9330		135.50	-230.6500	-313.6100
134.50	-60.7320	-140.4650		134.50	-220.5150	-299.7060
133.50	-58.0720	-134.2840		133.50	-210.8160	-286.0330
132.50		        -128.3450		133.00	-206.0800	-279.6640
132.00	-54.3030	-125.5330		132.00	-197.0500	-267.3660
131.00	-51.9270	-120.0150		131.00	-188.4130	-255.5850
130.00	-49.6620	-114.7500		130.00	-180.1390	-244.2880
128.00	-45.4210	-104.9110		128.00	-164.6400	-223.1900
126.00	-41.5550	-95.9450		126.00	-150.5300	-204.0060
124.00	-38.0300	-87.7600		124.00	-137.6900	-186.4830
122.00	-34.8100	-80.2900		122.00	-125.9700	-170.5440
120.00	-31.8780	-73.4860		120.00	-115.2900	-156.0020
118.00	-29.2060	-67.2900		118.00	-105.5500	-142.7470
116.00	-26.7690	-61.6400		116.00	-96.6900	-130.6987
114.00	-24.6392	-56.5000		114.00	-88.6240	-119.7218
112.00	-22.6060	-51.5000		112.00	-81.2700	-109.7030
110.00	-20.7550	-47.5500		110.00	-74.5700	-100.6170
105.00	-7.6170	        -38.4870		105.00	-60.3500	-81.2724
100.00	-13.6900	-31.3000		100.00	-49.0700	-65.9450
95.00	-11.2000	-25.6840		95.00	-40.1000	-53.7603
90.00	-9.2140	        -21.1000		90.00	-32.9500	-44.0770
85.00	-7.6170	        -17.4250		85.00	-27.3370	-36.3176
80.00	-6.3283	        -14.4650		80.00	-22.6950	-30.0751
70.00	-4.4300	        -10.1160		70.00	-15.8800	-20.9880
60.00	-3.1525   	-7.2000 		60.00	-11.3140	-14.8445
50.00	-2.2720 	-5.2060 		50.00	-8.1950 	-10.6612
40.00	-1.6530 	-3.8125 		40.00	-6.0240 	-7.7550
30.00	-1.2085 	-2.8200 		30.00	-4.4750 	-5.6980
20.00	-1.8830 	-2.1020 	 	20.00	-3.3570 	-4.2240
10.00	-0.6410 	-1.5740 		10.00	-2.3800 	-3.1460
0.00	-0.4590 	-1.1800 		0.00	-1.9360 	-0.3540


Rotation

 I= - 6.505 A			I= - 15.25 A			I= - 24 A			I= - 33 A	
 Theta    B 		        Theta    B		        Theta    B		        Theta    B
(degree) (G)                   (degree) (G)                    (degree) (G)                    (degree) (G)
0.00	0.0288		        0.00	-0.1150		        0.00	-0.1540		        0.00	-0.2640
55.00	-61.9200		55.00	-148.7800		55.00	-230.0300		55.00	-316.2940
55.50	-68.2600		55.25	-155.1740		55.50	-263.5000		55.25	-332.5850
55.60	-69.6200		55.40	-159.6800		55.40	-248.7940		55.30	-335.9620
55.55	-69.9400		55.45	-161.2270		55.60	-258.7300		55.40	-342.2980
56.00	-75.2000		55.50	-162.7950					        55.50	-348.8980
57.00	-91.6000		56.00	-179.4560		56.00	-279.6800		55.60	-355.9930
58.00	-112.0400		57.00	-218.6250		57.00	-341.2300		56.00	384.8570
59.00	-137.5000		58.00	-267.4440		58.00	-417.3400		57.00	-468.7430
60.00	-169.3500		59.00	-328.7500		59.00	-512.4800		58.00	-573.3970
61.00	-208.8200		60.00	-404.8500		60.00	-631.2200		59.00	-704.0110
62.00	-254.4200		61.00	-498.4100		61.00	-777.3000		60.00	-867.4160
63.00	-298.9400		62.00	605.4600		62.00	-944.5000		61.00	-1068.4410
64.00	-327.8700		63.00	-706.3700		63.00	-1102.0000		62.00	1297.4500
65.00	-340.4800		64.00	-771.0200		64.00	-1203.0000		63.00	-1514.5900
66.00	-345.0700		65.00	-299.3600		65.00	-1247.3000		64.00	1653.1900
67.00	-346.7200		66.00	-809.8500		66.00	-1263.7700		65.00	1714.0200
68.00	-347.3000		67.00	-813.6000		67.00	-1269.6000		66.00	1736.4600
69.00	-347.5400		68.00	-814.9900		68.00	-1271.8000		67.00	1744.4900
70.00	-347.6100		69.00	-815.4800		69.00	-1272.6800		68.00	1747.3940
72.00	-347.7000		70.00	-815.6800		70.00	-1273.0000		69.00	-1748.6040
74.00	-347.7800		72.00	-815.8400		72.00	-1273.3000		70.00	1749.0000
76.00	-347.9000		74.00	-816.0100		74.00	-1273.6000		72.00	1749.3300
78.00	-347.9200		76.00	-816.2300		76.00	-1273.9500		74.00	-1749.7370
80.00	-348.0000		78.00	-816.4200		78.00	-1274.2700		76.00	-1750.1000
82.00	-348.0200		80.00	-816.5400		80.00	-1274.5000		78.00	-1750.4300
84.00	0.0500		        82.00	-816.6400		82.00	-1274.7000		80.00	-1750.6940
86.00	-348.0700		84.00	-816.7200		84.00	-1274.8700		82.00	-1751.0460
88.00	-348.1000		86.00	-816.8700		86.00	-1275.1000		84.00	-1751.2660
90.00	-348.1200		88.00	-817.0000		88.00	-1275.3500		86.00	-1751.5740
92.00	-348.1200		90.00	-817.0800		90.00	-1275.5000		88.00	-1751.8930
94.00	-348.1300		92.00	-817.1700		92.00	-1275.6000		90.00	-1752.0800
96.00	-348.1200		94.00	-817.2500		94.00	-1275.7700		92.00	-1752.2120
98.00	-348.1000		96.00	-817.3100		96.00	-1275.9000		94.00	-1752.3660
100.00	-348.0700		98.00	-817.3200		98.00	-1275.8500		96.00	-1752.4760
102.00	-348.0400		100.00	-817.2600		100.00	-1275.7600		98.00	-1752.4210
103.00	-348.0100		102.00	-817.2100		102.00	-1275.6000		100.00	-1752.2230
104.00	-347.9200		103.00	-817.1200		103.00	-1275.4500		102.00	-1752.0030
105.00	-347.6700		104.00	-816.9100		104.00	-1275.1100		103.00	-1751.8050
106.00	-346.8200		105.00	-816.2700		105.00			        104.00	-1751.3320
107.00	-343.8600		106.00	-813.9200		106.00	-1270.3000		105.00	-1749.8250
108.00	-334.4600		107.00	-805.8400		107.00	-1257.6000		106.00	-1744.7540
109.00	-303.6700		108.00	-778.4700		108.00	-1214.5200		107.00	-1727.3300
109.50	-280.2300		109.00	-704.9500		109.00	-1099.7000		108.00	-1668.2600
110.00	-253.5100		109.50	-648.9400		109.50	-1012.5200		108.50	1604.0420
110.50	-226.2950		110.00	-587.0300		110.00	-915.9200		109.00	-1510.1900
111.00	-201.0330		110.50	-524.0800		110.50	-817.5300		109.50	1389.5200
112.00	-156.6420		111.00	-465.1000		111.00	-725.0000		110.00	-1256.9700
113.00	-122.1500		112.00	-362.9700		112.00	-565.5800		110.50	-1122.2200
113.50	-108.0300		113.00	-283.0300		113.00	-440.9100		111.00	-996.0170
114.00	-95.7700                 								112.00	-777.0400
115.00	-75.4300		114.00	-221.4100		114.00	-345.2400		113.00	-605.7040
116.00	-59.7560		115.00	-174.4670		115.00	-272.1800		113.50	-535.4470
116.25	-56.3900		116.00	-138.0970		116.00	-214.8900		114.00	-474.2650
116.30	-55.7380		116.25	-130.2390		116.25	-202.6770		115.00	-373.6700
116.40	-54.4500		116.30	-128.6700		116.30	-200.3710		116.25	-295.8560
116.35	-55.0800		116.40	-125.6880		116.40	-195.7000		116.30	-275.3740
116.33	-55.3180		116.50	-122.7610		116.50	-191.1400		116.35	-272.1400
180.00	-0.1100 	 	180.00	-0.1970 		117.00	-170.1670		116.40	-268.9280
                                                                180.00	-0.1900 		116.50	-262.6151
                                                                                                116.60	-256.8720
                                                                                                117.00	-233.8292
                                                                                                180.00	-0.2970


Mapping Origin

File:Hrrl wiki dipole map Origin File.txt

Mapping data and are under the curve

-6.5 A

Mapping at -6.5 Amp. 

S	B
mm	G
Beam	Magnetic 
Path   Field
0	-5.996
5	-7.024
10	-8.265
15	-9.766
20	-11.596
25	-13.836
30	-16.596
35	-20.011
40	-24.25
45	-29.55
50	-35.96
55	-44.25
60	-54.67
65	-67.776
70	-84.225
75	-104.806
80	-130.495
85	-162.485
90	-202.426
92	-221.08
94	-241.527
96	-263.96
98	-288.57
100	-315.31
102	-344.89
104	-377.23
105.11	-395.22
107.9	-447.35
110.68	-505.17
113.46	-576.45
116.24	-629.02
119.02	-686.3
121.81	-733.05
124.59	-766.68
127.37	-788.63
132.94	-809.26
138.5	-815.77
144.07	-817.76
149.63	-818.35
155.2	-818.59
166.33	-818.79
177.46	-819.04
188.58	-819.25
199.71	-819.45
210.84	-819.59
221.97	-819.72
233.1	-819.86
244.23	-820
255.36	-820.16
266.49	-820.3
277.62	-820.4
288.75	-820.43
294.32	-820.4
305.44	-820.38
311.01	-820.24
316.57	-819.74
322.14	-817.73
324.92	-815.06
327.7	-809.82
330.49	-799.64
333.27	-780.86
336.05	-749.13
338.83	-700.97
341.62	-639.14
344.4	-570.24
347.18	-500.24
349.96	-435.41
352.75	-377.2
355.53	-326.14
356.53	-305.79
358.53	-275.51
360.53	-248.38
362.53	-224.38
365.53	-192.56
368.53	-165.48
371.53	-142.4
372.53	-135.47
377.53	-105.75
382.53	-82.85
387.53	-65.196
392.53	-51.56
397.53	-41.05
402.53	-32.897
412.53	-21.705
422.53	-14.625
447.53	-6.12
472.53	-2.94

Area under the curve 

[4/18/2012 01:47 "" (2456035)]
integ1
 Input
   iy = [Book1]6A!(A"S",B"B")
   type = 0 (math:Mathematical Area)
   plot = 0
 Output
   oy = [Book1]6A!(,C"Integrated Y1")
   x1 = 0
   x2 = 472.53
   i1 = 1
   i2 = 85
   area = -90700.3274
   y0 = -353.05
   x0 = 272.06
   dx = 245.38386115956

-15.25 A

Mapping at -15.25 Amp. 

S	B
mm	G
Beam	Magnetic 
Path   Field
0	-5.996
5	-7.024
10	-8.265
15	-9.766
20	-11.596
25	-13.836
30	-16.596
35	-20.011
40	-24.25
45	-29.55
50	-35.96
55	-44.25
60	-54.67
65	-67.776
70	-84.225
75	-104.806
80	-130.495
85	-162.485
90	-202.426
92	-221.08
94	-241.527
96	-263.96
98	-288.57
100	-315.31
102	-344.89
104	-377.23
105.11	-395.22
107.9	-447.35
110.68	-505.17
113.46	-576.45
116.24	-629.02
119.02	-686.3
121.81	-733.05
124.59	-766.68
127.37	-788.63
132.94	-809.26
138.5	-815.77
144.07	-817.76
149.63	-818.35
155.2	-818.59
166.33	-818.79
177.46	-819.04
188.58	-819.25
199.71	-819.45
210.84	-819.59
221.97	-819.72
233.1	-819.86
244.23	-820
255.36	-820.16
266.49	-820.3
277.62	-820.4
288.75	-820.43
294.32	-820.4
305.44	-820.38
311.01	-820.24
316.57	-819.74
322.14	-817.73
324.92	-815.06
327.7	-809.82
330.49	-799.64
333.27	-780.86
336.05	-749.13
338.83	-700.97
341.62	-639.14
344.4	-570.24
347.18	-500.24
349.96	-435.41
352.75	-377.2
355.53	-326.14
356.53	-305.79
358.53	-275.51
360.53	-248.38
362.53	-224.38
365.53	-192.56
368.53	-165.48
371.53	-142.4
372.53	-135.47
377.53	-105.75
382.53	-82.85
387.53	-65.196
392.53	-51.56
397.53	-41.05
402.53	-32.897
412.53	-21.705
422.53	-14.625
447.53	-6.12
472.53	-2.94


Area under the curve 

[4/18/2012 02:17 "" (2456035)]
integ1
 Input
   iy = [Book1]15A!(A"S",B"B")
   type = 0 (math:Mathematical Area)
   plot = 0
 Output
   oy = [Book1]15A!(,C"Integrated Y1")
   x1 = 0
   x2 = 472.53
   i1 = 1
   i2 = 87
   area = -210413.9633
   y0 = -820.43
   x0 = 288.75
   dx = 245.25506096565

24 A

Mapping at - 24 A Amp. 

S	B
mm	G
Beam	Magnetic 
Path   Field
0	-9.243
5	-10.843
10	-12.773
15	-15.12
20	-17.98
25	-21.488
30	-25.808
35	-30.97
40	-37.575
45	-45.83
50	-56.175
55	-69.179
60	-85.536
65	-106.117
70	-131.394
75	-164.266
80	-204.61
85	-254.866
90	-317.34
92	-346.6
94	-378.67
96	-413.85
98	-452.39
100	-494.75
102	-541.15
104	-591.94
105.11	-615.64
107.9	-696.51
110.68	-787.1
113.46	-884.2
116.24	-979.92
119.02	-1069.3
121.81	-1142.4
124.59	-1195
127.37	-1229.2
130.15	-1249.7
132.94	-1261.3
138.5	-1271.5
144.07	-1274.7
149.63	-1275.7
155.2	-1276.2
166.33	-1276.7
177.46	-1277
188.58	-1277.5
199.71	-1277.9
210.84	-1278.2
221.97	-1278.4
233.1	-1278.7
244.23	-1279
255.36	-1279.2
266.49	-1279.44
277.62	-1279.56
288.75	-1279.52
294.32	-1279.46
299.88	-1279.4
305.44	-1279.26
311.01	-1279
316.57	-1278.17
322.14	-1275
324.92	-1270.8
327.7	-1262.6
330.49	-1246.67
333.27	-1217.4
336.05	-1167.8
338.83	-1092.5
341.62	-996.14
344.4	-888.66
347.18	-779.86
349.96	-679.2
352.75	-588.1
355.53	-508.2
356.53	-481.38
358.53	-433.77
360.53	-391.15
362.53	-353
365.53	-302.89
368.53	-260.44
371.53	-224.09
372.53	-213.18
377.53	-166.37
382.53	-130.298
387.53	-102.48
392.53	-81.009
397.53	-64.45
402.53	-51.6
412.53	-33.78
422.53	-22.83
447.53	-9.45
472.53	-4.46


Area under the curve 

[4/18/2012 02:22 "" (2456035)]
integ1
 Input
   iy = [Book1]24A!(A"S",B"B")
   type = 0 (math:Mathematical Area)
   plot = 0
 Output
   oy = [Book1]24A!(,C"Integrated Y1")
   x1 = 0
   x2 = 472.53
   i1 = 1
   i2 = 89
   area = -328194.84795
   y0 = -1279.56
   x0 = 277.62
   dx = 245.22443902201

33 A

Mapping at - 33 Amp. 

S	B
mm	G
Beam	Magnetic 
Path   Field
0	-11.425
5	-13.417
10	-15.828
15	-18.25
20	-22.315
25	-26.683
30	-31.873
35	-38.504
40	-46.74
45	-57.044
50	-69.95
55	-86.175
60	-106.593
65	-132.263
70	-164.517
75	-204.863
80	-255.216
85	-317.7
90	-395.93
92	-432.4
94	-472.48
96	-516.44
98	-564.64
100	-617.51
102	-675.33
104	-738.69
105.11	-767.57
107.9	-868.32
110.68	-980.56
113.46	-1101.2
116.24	-1220.8
119.02	-1331.6
121.81	-1422.5
124.59	-1487.8
127.37	-1530.3
130.15	-1558.4
132.94	-1570.3
138.5	-1582.9
144.07	-1586.9
149.63	-1588.2
155.2	-1588.74
166.33	-1589.3
177.46	-1589.8
188.58	-1590.37
199.71	-1590.73
210.84	-1591.05
221.97	-1591.4
233.1	-1591.8
244.23	-1592.07
255.36	-1592.3
266.49	-1592.4
277.62	-1592.7
288.75	-1592.7
294.32	-1592.6
299.88	-1592.46
305.44	-1592.3
311.01	-1592
316.57	-1590.9
322.14	-1586.97
324.92	-1581.7
327.7	-1571.5
330.49	-1551.8
333.27	-1515.25
336.05	-1453.6
338.83	-1360
341.62	-1239.46
344.4	-1105.5
347.18	-969.8
349.96	-844.62
352.75	-732.05
355.53	-632.51
356.53	-597.3
358.53	-538.2
360.53	-485.2
362.53	-437.7
365.53	-375.37
368.53	-322.4
371.53	-277.28
372.53	-263.9
377.53	-205.84
382.53	-161.1
387.53	-126.58
392.53	-99.94
397.53	-79.38
402.53	-63.56
412.53	-41.35
422.53	-27.64
447.53	-11.3
472.53	-5.193


Area under the curve 

[4/18/2012 02:23 "" (2456035)]
integ1
 Input
   iy = [Book1]30A!(A"S",B"B")
   type = 0 (math:Mathematical Area)
   plot = 0
 Output
   oy = [Book1]30A!(,C"Integrated Y1")
   x1 = 0
   x2 = 472.53
   i1 = 1
   i2 = 89
   area = -408481.827
   y0 = -1592.7
   x0 = 277.62
   dx = 245.24936698806

Effective B-Field

Effective B-field = (Area Under the Curve) / (Beam path in dipole)

Scan Current Area Under the Curve (G*mm) Beam path in dipole (mm) Effective B-field (G)
-6.50A -90700.3274 250.149315 -362.584752
-15.25A -210413.9633 250.149315 -841.153466
-24A -328194.84795 250.149315 -1 311.99579
-33 A -408481.827 250.149315 -1 632.95201


Coil current vs Electron Beam Energy

Magnet (or momentum) rigidity: [math] p = qB\rho [/math]

p is momentum of the particle. q is the charge of the particle. [math] \rho [/math] is the bending radius of the dipole. B is magnetic filed strength.

For an electron

Unit Conversion

[math] p [kg*m/s]= e*B*\rho [/math]

[math] p / (5.36704629 \times 10^{-19}) [GeV/C]= e*B*\rho [/math]

[math] p [GeV/C]= 0.299792458*B*\rho [/math]

1 Gauss is [math] 10^{-4} [/math] Tesla

Coil Current (Amp) dipole (m) Effective B-field (T) P [MeV/c]
-6.50 0.3185 -0.0362584752 3.46210054
-15.25 0.3185 -0.0841153466 8.03166116
-24 0.3185 -0.131199579 12.5274472
-33 0.3185 -0.163295201 15.5920623


[math] E^2= P^2 + m_e^2[/math]

Coil Current (Amp) P [MeV/c] En using field map (MeV) Corresponding En from table (MeV)
-6.50 3.46210054 3.49960871 2.403
-15.25 8.03166116 8.04790047 (6.129+6.350)/2
-24 12.5274472 12.5378648 10.095
-33 15.5920623 15.6004336 14.064 



Coil           En 
Current 
(Amp)          (MeV)
6.50 	 	3.49960871
15.25 	 	8.04790047
24 	 	12.5378648
33 	 	15.6004336

Fitting for En vs I

File:Hrrl-wiki-dip-mag-map-En vs I.png 400 px

matlab Poly fit method

       R: [3x3 double]
      df: 1
   normr: 0.9538


table = 

   3.4996    6.5000    6.6725   -0.1725
   8.0479   15.2500   14.6937    0.5563
  12.5379   24.0000   24.6903   -0.6903
  15.6004   33.0000   32.6935    0.3065

MATLAB Polyfit Fit for En vs I: En = 1.17221 + 1.17221I + 0.05121I^2


Matrix Inversion Method

Matrix Inversion Method Fit for En vs I: En = (1.94299+-2.50720) + (1.17221+-0.61575)I + (0.05121+-0.03189)I^2

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Kiwi_Dipole_Mappings&oldid=73850"