Go Back to All Lab Reports
DC Bipolar Transistor Curves
Data sheet for transistors.
Media:2N3904.pdf Media:2N3906.pdf


Using 2N3904 is more srtaight forward in this lab.
Transistor circuit
1.) Identify the type (n-p-n or p-n-p) of transistor you are using and fill in the following specifications.
I am going to use n-p-n transistor 2N3904. Below are some specifications from data shits for this type of transistor:
| Value
|
Description
|
| [math]V_{(BR)CEO} = 40\ V[/math] |
Collector-Base breakdown voltage
|
| [math]V_{(BR)EBO} = 6\ V[/math] |
Emitter-Base Breakdown Voltage
|
| [math]V_{(BR)CEO} = 40\ V[/math] |
Maximum Collector-Emitter Voltage
|
| [math]V_{(BR)CBO} = 60\ V[/math] |
Maximum Collector-Emitter Voltage
|
| [math]I_C = 200\ mA[/math] |
Maximum Collector Current - Continuous
|
| [math]P = 625\ mW[/math] |
Transistor Power rating([math]P_{Max}[/math])
|
| [math]h_{FE}\ min \ [/math] |
[math]h_{FE}\ max \ [/math] |
[math]I_C[/math], [math]V_{CE}[/math]
|
| 40 |
300 |
[math]I_C=0.1\ mA[/math], [math]V_{CE}=1.0\ V[/math]
|
| 70 |
300 |
[math]I_C=1\ mA[/math], [math]V_{CE}=1.0\ V[/math]
|
| 100 |
300 |
[math]I_C=10\ mA[/math], [math]V_{CE}=1.0\ V[/math]
|
| 60 |
300 |
[math]I_C=50\ mA[/math], [math]V_{CE}=1.0\ V[/math]
|
| 30 |
300 |
[math]I_C=100\ mA[/math], [math]V_{CE}=1.0\ V[/math]
|
2.) Construct the circuit below according to the type of transistor you have.
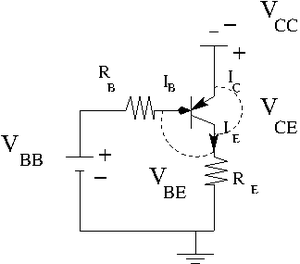
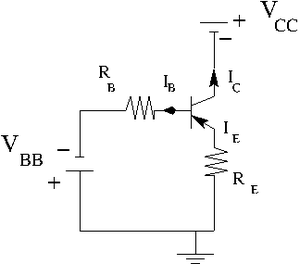
Let [math]R_E = 100 \Omega[/math].
[math]V_{CC} \lt 5 Volts[/math] variable power supply
[math]V_{BE}= 1\ V[/math].
Find the resistors you need to have
[math]I_B = 2 \mu A[/math] , [math]5 \mu A[/math] , and [math]10 \mu A[/math]
By measurements I was able to find that [math]V_{BE}= 0.6\ V[/math]. So I am going to use this value. Also let picks up [math]V_{BB}= 1.6\ V[/math]. So my current [math]I_B = \frac{V_{BB} - V_{BE}}{R_B} = \frac{(1.6 - 0.6)\ V}{R_B} = \frac{1.0\ V}{R_B}[/math].
Now to get [math]I_B = 2\ \mu A[/math] I need to use [math]R_B = \frac{1.0\ V}{2\ \mu A} = 500\ k\Omega[/math]
To get [math]I_B = 5\ \mu A[/math] I need to use [math]R_B = \frac{1.0\ V}{5\ \mu A} = 200\ k\Omega[/math]
To get [math]I_B = 10\ \mu A[/math] I need to use [math]R_B = \frac{1.0\ V}{10\ \mu A} = 100\ k\Omega[/math]
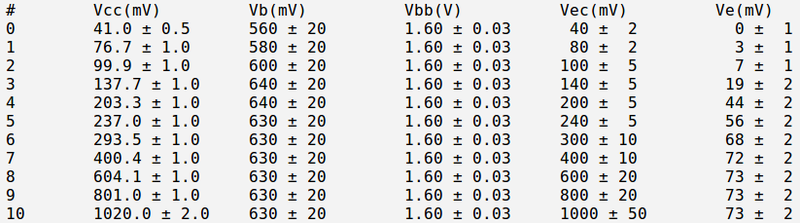
3.) Measure the emitter current [math]I_E[/math] for several values of [math]V_{CE}[/math] by changing [math]V_{CC}[/math] such that the base current [math]I_B = 2 \mu[/math] A is constant. [math]I_B \approx \frac{V_{BB}-V_{BE}}{R_B}[/math]
I used:
[math]R_1 = (199.5 \pm 1.0)\ k\Omega [/math]
[math]R_1 = (198.7 \pm 1.0)\ k\Omega [/math]
[math]R_1 = (100.0 \pm 1.0)\ k\Omega [/math]
[math]R_B = (R_1 + R_2 + R_3) = (498.2 \pm 1.7)\ k\Omega [/math]
and
[math]R_E = (100.0 \pm 1.0)\ \Omega [/math]
Below is the table with my measurements:
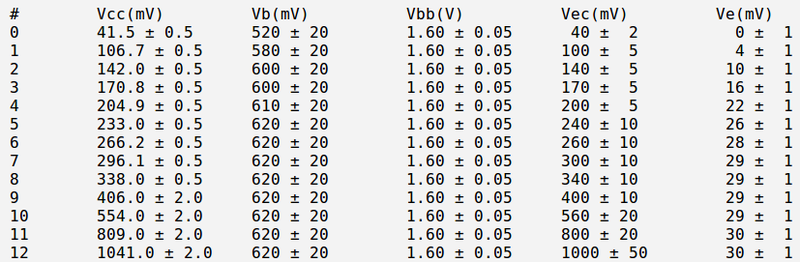
And below is my currents and power calculation:
Here:
[math]I_{E} = \frac{V_E}{R_E}[/math]
[math]I_{B} = \frac{V_{BB}-V_B}{R_B}[/math]
[math]P_{max} = I_C \cdot V_{EC} = (I_E - I_B) \cdot V_{EC} [/math]
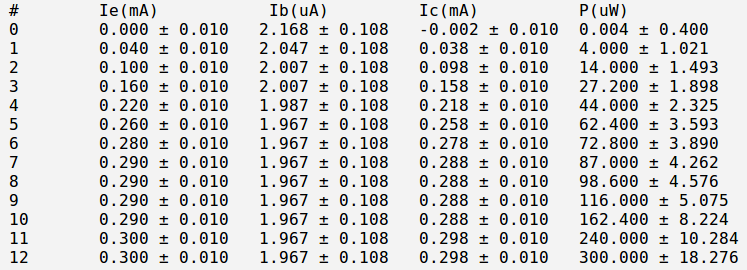
4a.) Repeat the previous measurements for [math]I_B \approx 5\ \mu A[/math]. Remember to keep [math]I_CV_{CE} \lt P_{max}[/math] so the transistor doesn't burn out
I used:
[math]R_B = (199.5 \pm 1.0)\ k\Omega [/math]
and
[math]R_E = (100.0 \pm 1.0)\ \Omega [/math]
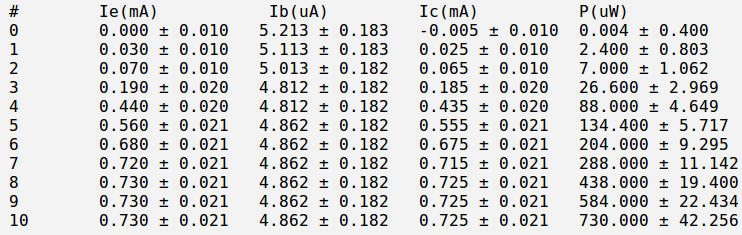
Below is the table with my measurements:
And below is my currents and power calculation:
Here:
[math]I_{E} = \frac{V_E}{R_E}[/math]
[math]I_{B} = \frac{V_{BB}-V_B}{R_B}[/math]
[math]P_{max} = I_C \cdot V_{EC} = (I_E - I_B) \cdot V_{EC} [/math]
4a.) Repeat the previous measurements for [math]I_B \approx\ 10 \mu A[/math]. Remember to keep [math]I_CV_{CE} \lt P_{max}[/math] so the transistor doesn't burn out
I used:
[math]R_B = (100.0 \pm 1.0)\ k\Omega [/math]
and
[math]R_E = (100.0 \pm 1.0)\ \Omega [/math]
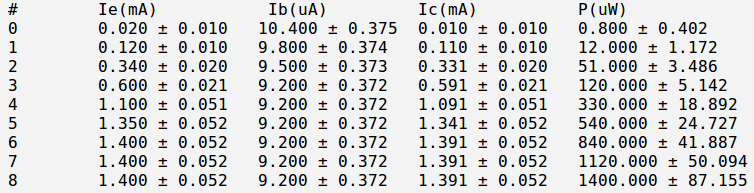
Below is the table with my measurements:

And below is my currents and power calculation:
Here:
[math]I_{E} = \frac{V_E}{R_E}[/math]
[math]I_{B} = \frac{V_{BB}-V_B}{R_B}[/math]
[math]P_{max} = I_C \cdot V_{EC} = (I_E - I_B) \cdot V_{EC} [/math]
5.) Graph [math]I_C[/math] -vs- [math]V_{CE}[/math] for each value of [math]I_B[/math] and [math]V_{CC}[/math] above. (40 pnts)
Bellow is my plot for the case of [math]I_B = 2 \mu A[/math]
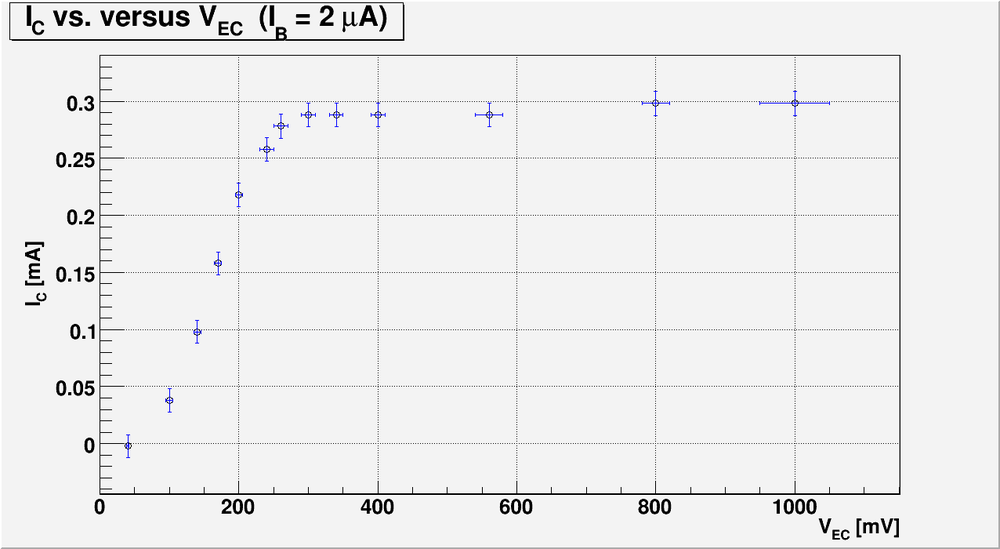
Bellow is my plot for the case of [math]I_B = 5 \mu A[/math]
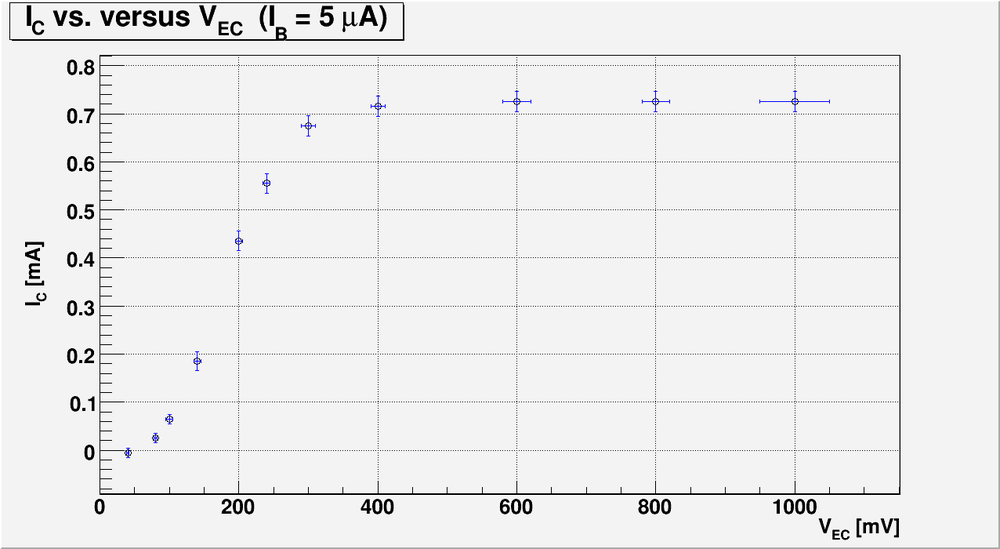
Bellow is my plot for the case of [math]I_B = 10 \mu A[/math]
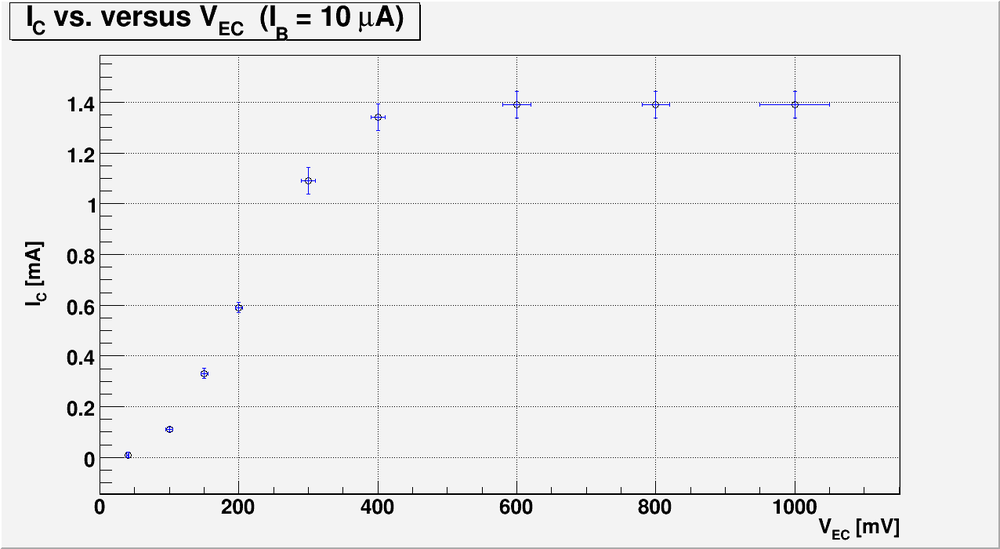
6.) Overlay points from the transistor's data sheet on the graph in part 5.).(10 pnts)
Questions
- Compare your measured value of [math]h_{FE}[/math] or [math]\beta[/math] for the transistor to the spec sheet? (10 pnts)
I will calculate my [math]\beta[/math] from my measurements above in saturation region:
1)[math]I_B = 2\ \mu A[/math]: [math]\beta = \frac{I_C}{I_B} = \frac{(0.298 \pm 0.010) mA}{(1.967 \pm 0.108) uA} = (151 \pm 9) [/math]
2)[math]I_B = 2\ \mu A[/math]: [math]\beta = \frac{I_C}{I_B} = \frac{(0.725 \pm 0.021) mA}{(4.862 \pm 0.121) uA} = (149 \pm 6) [/math]
3)[math]I_B = 2\ \mu A[/math]: [math]\beta = \frac{I_C}{I_B} = \frac{(1.391 \pm 0.052) mA}{(9.200 \pm 0.372) uA} = (151 \pm 8) [/math]
- What is [math]\alpha[/math] for the transistor? [math]\alpha = \frac {I_{C}}{I_{E}}[/math] (10 pnts)
- The base must always be more positive (negative) than the emitter for a npn (pnp) transistor to conduct I_C.(10 pnts)
- For a transistor to conduct I_{C} the base-emitter junction must be forward biased.(10 pnts)
- For a transistor to conduct I_{C} the collector-base junction must be reversed biased.(10 pnts)
Measure the Base-Emitter breakdown voltage. (10 pnts)
I expect to see a graph [math](I_{B} -vs- V_{BE} )[/math] and a linear fit which is similar to the forward biased diode curves. Compare your result to what is reported in the data sheet.
I used:
[math]R_B = (199.5 \pm 1.0)\ k\Omega [/math]
[math]R_E = (100.0 \pm 1.0)\ \Omega [/math]
[math]V_{CC} = (840 \pm 20)\ mV [/math]
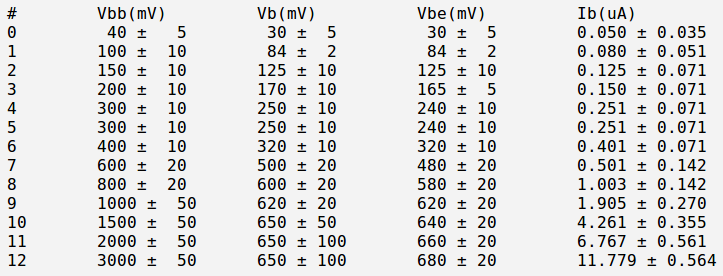
Below is the table with my measurements and current calculations:
Here:
[math]I_{B} = \frac{V_{BB}-V_B}{R_B}[/math]
And bellow is my plot for the Base-Emitter breakdown voltage
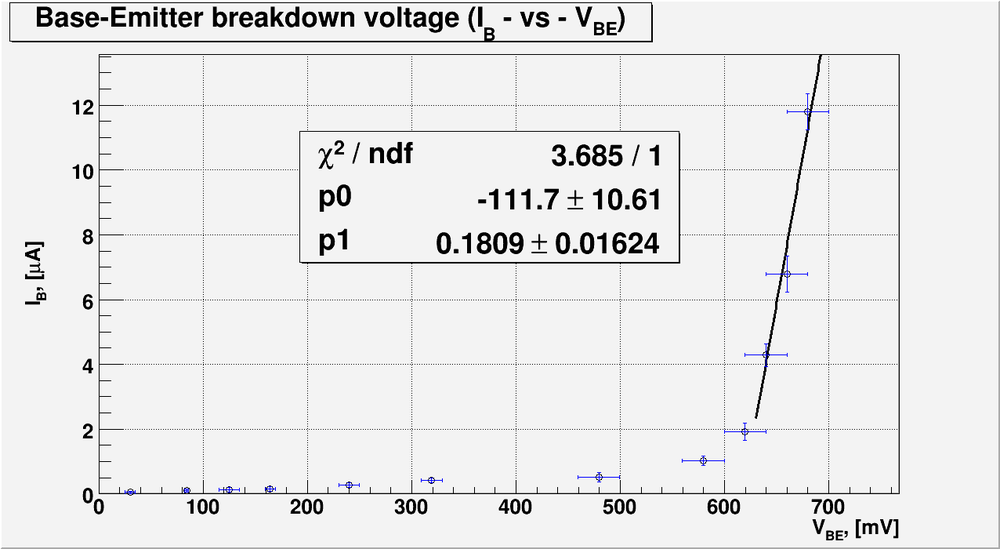
The fitting line is [math]I_B[\mu A] = (111.7 \pm 10.61) + (0.1809 \pm 0.01634)[mV] [/math]. The intersection this line with x-axis gives the forvard turn on voltage:
[math]V_{turn\ on} = \frac{p_0}{p_1} = \frac{111.7 \pm 10.61}{0.1809 \pm 0.01634} = (617.46 \pm 80.93)[mV][/math]
Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement














