Lab 4 RS

Go Back to All Lab Reports

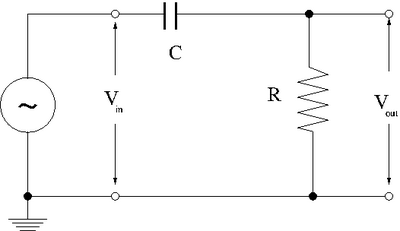
RC High-pass filter

1-50 kHz filter (20 pnts)

1. Design a high-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter's attenuation of the AC signal goes to 0(not passed). For a High pass filter, AC signals with a frequency below the 1-50 kHz range will be attenuated .

To design low-pass RC filter I had:

[math]R=10.5\ \Omega[/math]  
[math]C=1.250\ \mu F[/math]

So

[math]\omega_b = \frac{1}{RC} = 76.19\cdot 10^3\ \frac{rad}{s}[/math]
[math]f_b = \frac{\omega_b}{2\pi} = 12.13\ \mbox{kHz}[/math]

2. Now construct the circuit using a non-polar capacitor.

3. Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter.

4. Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz.

Table1. Voltage gain vs. frequency measurements

[math]\nu\ [\mbox{kHz}][/math]	[math]V_{in}\ [V][/math]	[math]V_{out}\ [V][/math]	[math]\frac{V_{out}}{V_{in}}[/math]
0.1
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
11.0
12.0
15.0
20.0
30.0
40.0
50.0
100.0
200.0

5. Graph the [math]\log \left(\frac{V_{out}}{V_{in}} \right)[/math] -vs- [math]\log (\nu)[/math]

phase shift (10 pnts)

1. measure the phase shift between [math]V_{in}[/math] and [math]V_{out}[/math]

Questions

Calculate and expression for [math]\frac{V_{out}}{ V_{in}}[/math] as a function of [math]\nu[/math], [math]R[/math], and [math]C[/math].(5 pnts)

We have:

[math]1)\ V_{in} = I \left(R+R_C\right) = I\left(R+\frac{1}{i\omega C}\right)[/math]

[math]2)\ V_{out} = I R [/math]

Dividing second equation into first one we get the voltage gain:

[math]\ \frac{V_{out}}{V_{in}} = \frac{I R}{I\left(R+\frac{1}{i\omega C}\right)} = \frac{i\omega RC}{1 + i\omega RC}[/math]

And we are need the real part:

[math]\left |\frac{V_{out}}{V_{in}} \right | = \sqrt{ \left( \frac{V_{out}}{V_{in}} \right)^* \left( \frac{V_{out}}{V_{in}} \right)} = \sqrt{\left ( \frac{i\omega RC}{1 + i\omega RC}\right ) \left ( \frac{-i\omega RC}{1 - i\omega RC}\right )} = \frac{\omega RC}{\sqrt{(1 + (\omega RC)^2}} = \frac{\omega RC}{\sqrt{(1 + (2\pi\nu RC)^2}}[/math]

Compare the theoretical and experimental value for the phase shift [math]\theta[/math]. (5 pnts)

The experimental phase shift is [math]\ \Theta_{exper} = (\omega\ \delta T)_{exper}[/math]

The theoretical phase shift is [math]\ \Theta_{theory}=\arctan\ \left (\frac{1}{\omega R C}\right )[/math]

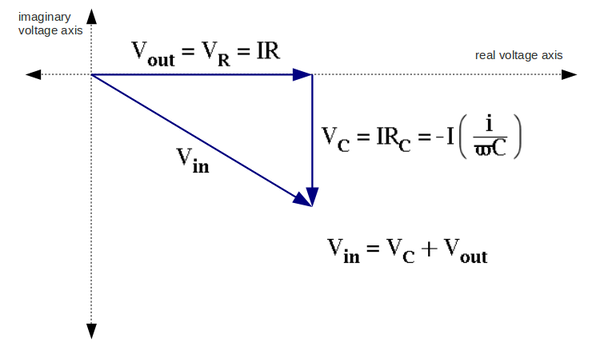
Sketch the phasor diagram for [math]V_{in}[/math],[math] V_{out}[/math], [math]V_{R}[/math], and [math]V_{C}[/math]. Put the current [math]I[/math] along the real voltage axis. (30 pnts)

What is the phase shift [math]\theta[/math] for a DC input and a very-high frequency input?(5 pnts)

Because a DC circuit doesn't have any oscillation there are no any phase shift.

Calculate and expression for the phase shift [math]\theta[/math] as a function of [math]\nu[/math], [math]R[/math], [math]C[/math] and graph [math]\theta[/math] -vs [math]\nu[/math]. (20 pnts)

From the phasor diagram above (question 4) the angle between vectors [math]V_{in}[/math] and [math]V_{out}[/math] given by

[math]\Phi = \arctan \ (V_C/V_R) = =\arctan \left( \frac{I \left|\frac{1}{i\omega C}\right|}{IR} \right) = \arctan \left ( \frac{1}{\omega RC} \right )[/math]

Forest_Electronic_Instrumentation_and_Measurement Go Back to All Lab Reports