Go Back
condition 1: fitting the collimator size into the hole
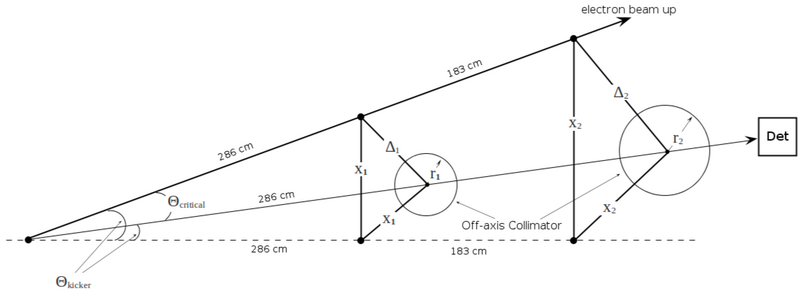
The minimum energy of accelerator (MeV) is limited by fitting the collimator size [math]r_2[/math] into the hole R = 8.73 cm:
[math]x_2 + r_2 = R[/math]
1) Assuming the collimator diameter is [math]\Theta_C[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV [/math]
2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV [/math]
3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/2[/math]:
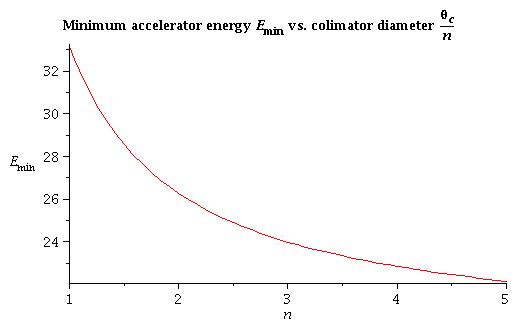
All energy under this line is good to run experiment for condition above
condition 2: F1A = 286 cm
1) assuming the collimator diameter is [math]\Theta_C[/math]
[math] E_{min} = 73.7\ MeV [/math]
2) assuming the collimator diameter is [math]\Theta_C/2[/math]
[math] E_{min} = 36.9\ MeV [/math]
3) assuming the collimator diameter is [math]\Theta_C/4[/math]
[math] E_{min} = 18.4\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/m[/math]:
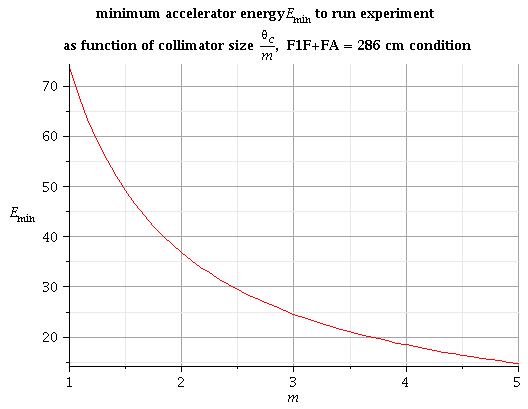
All energy under this line is good to run experiment for condition abov
both conditions above are together
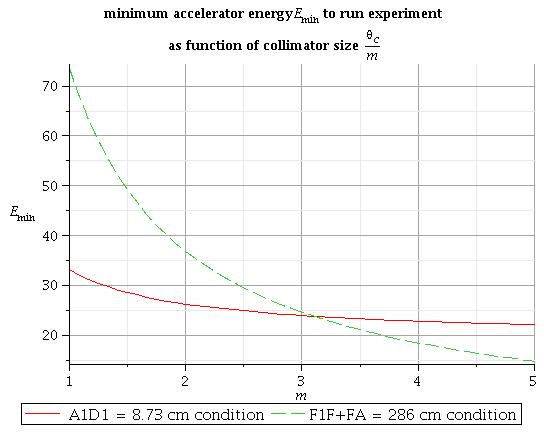
All energy above this lines is good to run experiment
Go Back



