Go Back
Minimum accelerator energy to run experiment
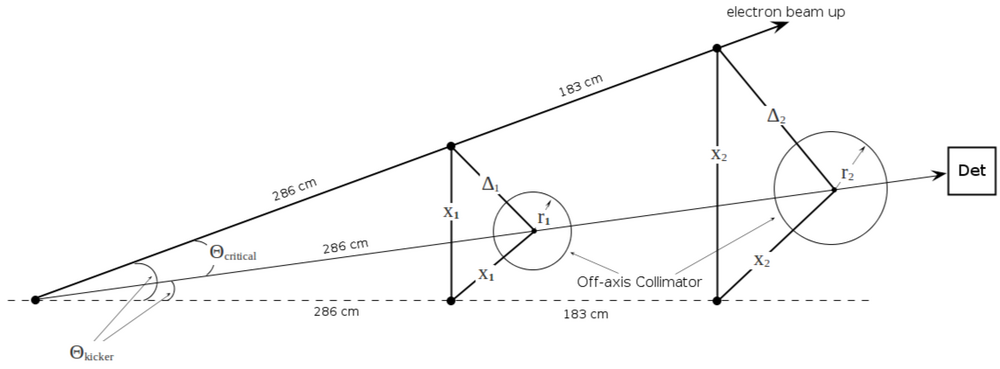
The minimum energy of accelerator (MeV) is limited by fitting the collimator ([math]r_2[/math]) into the hole ([math]R = 8.73\ cm[/math])
[math]x_2 + r_2 = R[/math]
1) Assuming the collimator diameter is [math]\Theta_C[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV [/math]
2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV [/math]
3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV [/math]
4) In general:
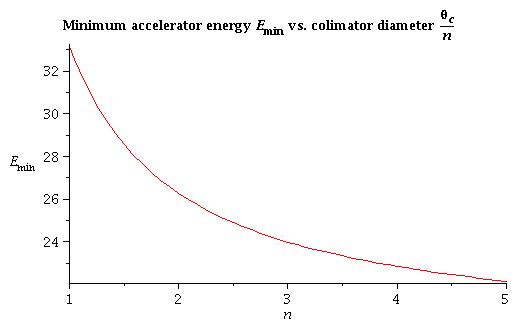
25 MeV geometry
geometry calculation
| collimator diameter
|
[math]\Theta_{critical}[/math]
|
[math]\Theta_{kicker}[/math]
|
[math]\alpha_{collimator}[/math]
|
[math]AC[/math]
|
[math]A_1C_1[/math]
|
[math]BD[/math]
|
[math]B_1D_1[/math]
|
| [math]\frac{\Theta_{critical}}{2}[/math] |
[math]1.17^o[/math] |
[math]0.83^o[/math] |
[math]2.03^o[/math] |
4.13 |
6.78 |
2.92 |
4.79
|
| [math]\frac{\Theta_{critical}}{4}[/math] |
[math]1.17^o[/math] |
[math]0.82^o[/math] |
[math]1.43^o[/math] |
4.13 |
6.78 |
1.46 |
2.40
|
geometry pictures
how it looks 1 ([math] \Theta_c/2[/math], box 3"x4" and then pipe 4")
File:Vacuum pipe collimator .png
how it looks 2 ([math] \Theta_c/4[/math], box 3"x4" and then pipe 4")
File:Vacuum pipe collimator .png
Go Back

