Go Back
Counts Rate for U238
LINAC parameters used in calculations
1) pulse width 50 ps
2) pulse current 50 A
3) repetition rate 300 Hz
4) energy 44 MeV
Number of electrons/sec on radiator
[math] 50\ \frac{Coulomb}{sec} \times \frac{1\cdot e^-}{1.6\cdot 10^{-19}C} \times 50ps \times 300Hz = 0.47 \cdot 10^{13} \frac{e^-}{sec}[/math]
Number of photons/sec on target
bremsstrahlung
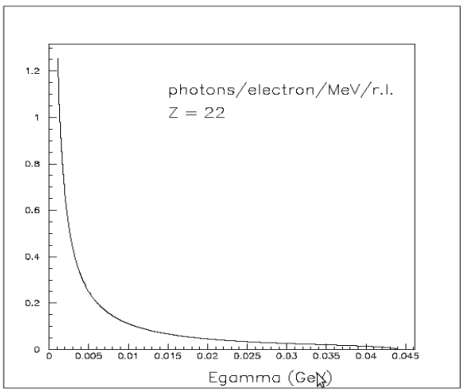
in (10,20) MeV region we have about
0.1 photons/electrons/MeV/r.l
radiation length
r.l.(Ti) = 3.59 cm
radiator thickness = 12.5 [math]\mu m[/math]
[math]12.5\mu m/3.59 cm = 3.48 \cdot 10^{-4} \ r.l.[/math]
steps together...
[math]0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 3.48 \cdot 10^{-4} r.l. \times 10\ MeV \times 0.47 \cdot 10^{13} \frac{e^-}{sec}=1.64 \cdot 10^{9} \frac{\gamma}{sec}[/math]
Alex factor (GEANT4 calculation)
Collimation factor is
6.85 % of total # of photons
then, incident flux on target is
[math]1.64 \cdot 10^{9} \frac{\gamma}{sec} \cdot 6.85\ % = 11.2 \cdot 10^{7} \frac{\gamma}{sec}[/math]
Number of neutrons/sec (yields)
photonuclear cross section for [math]^{238}U(\gamma , n)[/math] reaction
From the paper "Giant resonance for the actinide nuclei: Photoneutron and photofission cross sections for 235U, 236U, 238U, and 232Th", J. T. Caldwell and E. J. Dowdy, B. L. Berman, R. A. Alvarez, and P. Meyer. Physical Review C, (21), 1215, April 1980:
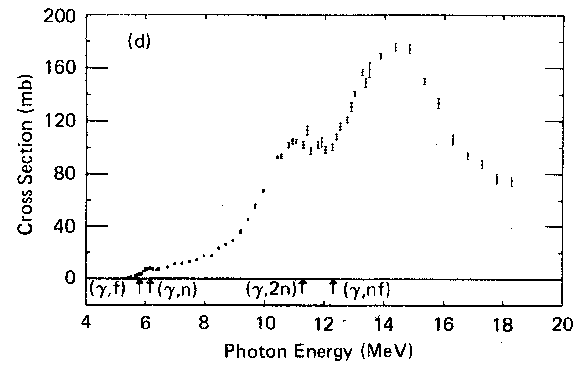
in (10,20) MeV region the average cross section, say, is:
130 mb
target thickness, [math]^{238}U[/math]
[math]\frac{19.1\ g/cm^3}{238.02\ g/mol} = 0.08\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ atoms}{mol} = 0.48\cdot 10^{23}\ \frac{atoms}{cm^3}[/math]
Target thickness = 1 cm:
[math]0.48\cdot 10^{23}\ \frac{atoms}{cm^3} \times 1\ cm = 0.48\cdot 10^{23}\ \frac{atoms}{cm^2}[/math]
neutrons per fission
2.4 neutrons/fission
steps together...yeild
[math] Y = \frac{\gamma}{sec} \times t \times \sigma \times 2.4 = [/math]
[math] = 11.2 \cdot 10^{7} \frac{\gamma}{sec} \times 130\ mb \times 0.48\cdot 10^{23}\ \frac{atoms}{cm^2} \times 2.4 = 1.68 \cdot 10^{6}\ \frac{neutrons}{sec}[/math]
Worst Case Isotropic Neutrons
checking detector distance
we want:
the time of flight of neutron >> the pulse width
take the worst case 10 MeV neutron:
[math] E_{tot} = E_{kin} + E_{rest} = 10\ MeV + 938\ MeV = 948\ MeV [/math]
[math] \gamma = \frac{E_{tot}}{m_p} = \frac{948\ MeV}{938\ MeV} = 1.0107 [/math]
[math] \gamma^2 = \frac{1}{1 - \beta^2} \ \ \ \rightarrow \ \ \ \beta = 0.145\ c[/math]
take the neutron detector 1 meter away:
[math] t = \frac{1\ m}{0.145\ c} = \frac{1\ m}{0.145\cdot 3\cdot 10^8\ m/sec} = 23\ ns [/math]
23 ns >> 50 ps <= time resolution is good
geometrical factor
taking real detector 3" x 2" => S is about 40 cm^2
1 meter away
fractional solid angle = [math]\frac{\pi * 40\ cm^{2}}{4 \pi\ (100\ cm)^{2}} = \frac{1}{4} \cdot 10^{-4}[/math] <= geometrical acceptance
Yield
the yield per second:
[math]1.2 \cdot 10^{6}\ \frac{neutrons}{sec} \times \frac{1}{4} \cdot 10^{-4} = 30\ \frac{neutrons}{sec} [/math]
the yield per pulse:
[math] 30\ \frac{neutrons}{sec} \times \frac{1\ sec}{300\ pulses} = 0.1\ \frac{neutrons}{pulse} [/math]
30 neutrons/sec <= this experiment is do able
0.1 neutrons/pulse <= good for stopping pulse
Counts Rate for Deuteron
Photonuclear cross section for [math] ^2H(\gamma , n) [/math] reaction=
From the paper "Absolute total cross sections for deuteron photodisintegration between 7 and 19 MeV", A. De Graeva and other. Physical Review C, (45), 860, February 1992:
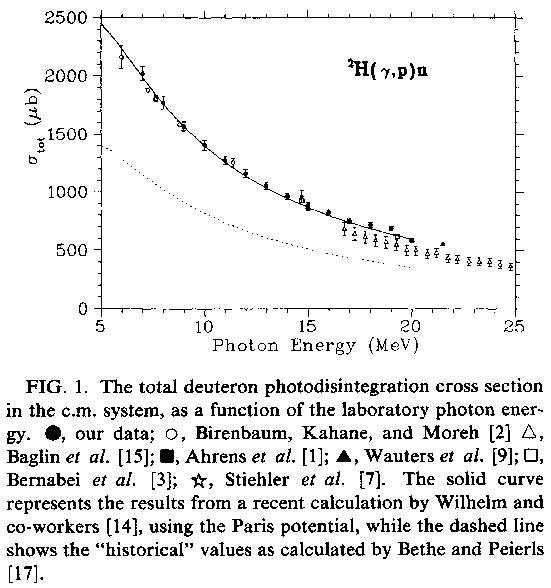
in (10,20) MeV region the average cross section, say, is:
1000 mb
target thickness, [math] D_2O [/math]
take [math]D_2O[/math], liquid (20°C):
[math] \frac{1.1056\ g/mL}{20.04\ g/mol} = 0.055\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ molecules}{mol} = 0.33\cdot 10^{23}\ \frac{molecules}{cm^3} [/math]
[math] 0.33\cdot 10^{23}\ \frac{molecules}{cm^3} \times \frac{2\ deuterons}{molecule} = 0.66\cdot 10^{23}\ \frac{deuterons}{cm^3} [/math]
Target thickness = 1 cm:
[math]0.66\cdot 10^{23}\ \frac{atoms}{cm^3} \times 1\ cm = 0.66\cdot 10^{23}\ \frac{atoms}{cm^2}[/math]
Calibration factor
The only difference from calculations above is:
1. cross section:
1000 mb (D) / 130 mb (238U) = 1000/130
2. target thickness:
[math] \frac{0.66\cdot 10^{23}\ atoms/cm^2\ (D)}{0.48\cdot 10^{23}\ atoms/cm^2\ (238U)} = 0.66/0.44 [/math]
3. neutrons per reaction:
1 neutron (D) / 3 neutrons(238U) = 1/3
total calibration factor is:
1000/130 * 0.66/0.44 * 1/3 = 3.8
Yield
saying all other factors is the same =>
the yield per second :
[math] 30\ \frac{neutrons}{sec} \times 3.8 = 114\ \frac{neutrons}{sec} [/math]
the yield per pulse:
[math] 114\ \frac{neutrons}{sec} \times \frac{1\ sec}{300\ pulses} = 0.4 \frac{neutrons}{pulse} [/math]
Go Back


