PhD Proposal Tamar
Tamar PhD Proposal
Abstract
Semi-inclusive deep inelastic scattering experiments using longitudinally polarized hydrogen () and deuterium () targets and a longitudinally polarized electron beam can be used to measure the ratio of the polarized valence quark distribution function to the unpolarized. Semi-inclusive scattering identifies an electron scattering experiment in which the scattered electron and one hadron are detected in the final state. I propose to analyze an electron scattering data set collected using the CEBAF Large Acceptance Spectrometer (CLAS) at Thomas Jefferson National Laboratory. The incident electron energy ranged between 1.6 GeV to 5.7 GeV. The electons impinged on either polarized proton or deuteron target. This work focuses on a kinematic region where the struck quark carries at least 30% of the nucleons total momentum . The leptons scatter mostly from valence quarks in this kinematic region allowing contributions from sea quarks to be neglected. The above measurements are able to distinguish between the predictions made by the hyperfine perturbed quark constituent model (pQCM) and perturbative Quantum Chromodynamics (pQCD). As a result, the following study can be used to test the validity of the above models describing the structure of the nucleon.
Introduction
The mid 1960's were a revolutionary period in the physics of elementary particles in which the field was challenged to explain the list of particles which became known as the "particle zoo". The most successful scheme to explain the "particle zoo" was proposed by the Gell-Mann and Ne'eman, the ansatz scheme. The scheme classified hadrons in group-theoretical terms as multiplets of the special unitary Lie group SU(3), using as the relevant quantum numbers, such as isospin, baryon number and strangeness.
what is the sentence below trying to say?
However, the ansatz scheme had classified hadrons, which were in the higher dimensional representations of SU(3), the fundamental ones were empty. In order to solve this problem Gell-Mann Zweig stated that a set of three particles which were the fundamental representations of the SU(3) group should also exist, so called quarks. According to the SU(3) they carry the fractional charge and . The quantum numbers of those new particles, which represent their properties, were u(up), d(down) and s(strange). At the time experimental evidence to support their existence was not present.
Electron scattering has been used for more than 40 years to measure the structure of a nucleon, a neutron or a proton. The early experiments at the Stanford Linear Accelerator Center (SLAC) showed that a nucleon(hadron) was really composed of constituents called quarks. The constituent quark model describes a baryon as a combination of three quarks and mesons as a quark-antiquark bound state. According to the quark model, two of the three quarks in a proton are labeled as having a flavor "up" and the remaining quark a flavor "down". The two up quarks have fractional charge while the down quark has a charge All quarks have spin . In the quark model each quark carries one third of the nucleon mass.
While elastic scattering measures the ground state properties of a nucleon, inelastic scattering experiments are used to probe a nucleon's excited states. The experiments at the SLAC used high energy electrons scattered by nucleons. The mediator between the target nucleon and coulomb scattering of an electron is the virtual photon. The four-momentum, Q, of the virtual photon serves as a measure of the resolution of the scattering and may be formulated as:
The electron scattering data taken during the SLAC experiments revealed a scaling behavior, which was later defined as Bjorken scaling. The inelastic cross section was anticipated to fall sharply with like the elastic cross section. The limited dependence, scaling, observed suggested that the nucleons constituents are pointlike.
Independently, Richard Feynman introduced the quark parton model where the nucleons, a proton or neutron, are constructed by the three point like constituents, which were called partons.
Shortly afterwards, it was discovered that partons and quarks are the same particles. In the QPM the mass of the quark is much smaller than in the naive quark model. In the parton model the inelastic electron nucleon interaction via the virtual photon is understood as an incoherent elastic scattering processes between the electron and the constituents of the target nucleon. "In other words, one assumes that a single interaction does not happen with the nucleon as a whole, but with exactly one of its constituents."<ref> G. Dissertori, I.K. Knowles, M. Schmelling, Quantum Chromodynamics: High energy experiments and theory, International Series of Monographs on Physics No. 115, ISBN 0198505728, Oxford University Press, Feb. 2003.</ref> In addition, two categories of quarks were introduced, "sea" and "valence" quarks. The macroscopic properties of the particle is determined by its valence quarks. The valence quarks in the proton are the up, up and down quarks. On the other hand, the so called sea quarks, virtual quarks and antiquarks, are constantly created from the vacuum.
the QCD paragraph below seems out of place, you devoted several paragraph to CQM an one to QCD
A new theory, called quantum chromodynamics(QCD), proposed that in addition to the sea and valence quarks, there are neutral particles, gluons, that bind quarks together. Gluons are able to interact with each other and create virtual quark anti-quarks pairs. In 1979, evidence of gluons was discovered in a "three jet event" at PETRA . <ref>http://en.wikipedia.org/wiki/Three_jet_event</ref>
Baryon resonances were reproduced partially by the models described above. The constituent quark model can reproduce the octet and decuplet baryons, which represent the ground states with respect to the orbital motion of the quarks. In addition, the negative-parity baryon resonances, which are the spatial excitation of the quarks are well classified by the constituent quark model.<ref> M. Arima, K. Masutani, T. Sato, Progress of Theoretical Physics Supplement, No. 137, pp. 169-188 </ref> However, the masses of particular resonances, such as A(1405) and N(1440) have not been shown by the CQM. On the other hand, lattice QCD gives access to the N(1440) baryon resonance and others.
The understanding of the spin structure in the nucleon remains a major challenge for hadron physics. The parton model predicted that quarks carry about 60 % of the
define acronyms below
total nucleon spin. Experiments performed at CERN by EMC found out that only 12 % of the nucleon spin is carried by the quarks. Other experiments at CERN(SMC) and SLAC(E142 && E143) did not agree with the naive quark parton model. "This reduction is often attributed to the effect of a negatively polarized quark sea at low momentum fraction x, which is typically not included in quark models." The complete picture of the nucleon spin can be obtained by taking into account the spin contributions from the gluons, the sea quarks and in addition the quarks orbital momentum. So the spin of the nucleon can be written as the sum of the following terms<ref>B. Hommez, Ph.D Thesis, University of Gent (2003).</ref>:
where is the spin contribution from the quarks, - from the gluons and - the orbital angular momentum contribution from the partons(quarks).
Physics Motivation
In inclusive deep inelastic scattering only the electron is detected in the final state and in the case of semi inclusive deep inelatic scattering the hadron is detected in coincidence with the scattered electron. Both physics processes can be characterized by the differential cross section. The cross section is equivalent to the detection rate. The differential cross section for the inclusive deep inelastic scattering can be written in terms of a lepton and a hadronic ( tensor<ref> R. G. Roberts, The structure of the proton, Cambridge Monographs on Mathematical Physics, ISBN 0521351596, Cambridge University Press, 1990.</ref> :
where the leptonic tensor describes the coupling between the scattering lepton and the virtual photon. The hadronic tensor - the absorption of the virtual photon by the target nucleon. The hadronic tensor contains the information about the nucleon structure. It can be written in terms of structure functions using symmetry arguments and conservation laws. However, the information about the spin distribution inside the nucleon is contained in the asymmetric part of the hadronic tensor, which can be obtained by taking the difference of the cross sections with opposite spin states of the initial electron beam.
The double spin asymmetry can be defined as the difference between the cross section observed when the spin of the initial electron beam is antiparallel and parallel to the target nucleon spin divided by the sum.<ref name="Airapetian2005"> A. Airapetian et al. (HERMES), Phys. Rev. D 71, 012003 (2005), hep-ex/0407032.</ref>
where the cross section difference for polarized case is given by
where E and are the initial and final energy of the electron, - the electron scattering angle, - the four momentum transferred square, x and y - bjorken scaling variables, and and polarized structure functions, which contain information on the spin structure of the nucleon.
Measurement of the double spin asymmetry and the ratio of the polarized valence down quark distribution function to the unpolarized can be used to distinguish between two descriptions of nucleon structure.
pQCD and a hyperfine perturbed constituent quark model both predict that when the scaling variable = 1, the proton and neutron double spin asymmetries ~1. On the other hand, the well-studied SU(6) constituent quark model for =1 states that and . Semi inclusive double spin asymmetry measurements using the CLAS Detector in combination with polarized proton and deuteron targets can be used to distinguish between prediction of pQCD and the hyperfine perturbed CQM, unlike inclusive scattering were they have the same prdictions.<ref> K.V. Dharmawardane et al., (The CLAS Collaboration), Phys. Lett. B 641, 11 2006, nucl-ex/0605028</ref> <ref name="Forest">T. A. Forest, Measurement of Polarized Valence Quark Distribution Functions using Polarized Proton and Deuteron Targets with CLAS, 2000.</ref>
Deep inelastic scattering has provided a wealth of information about the quark gluon structure. Inclusive deep inelastic lepton-nucleon scattering experiments were used to measure the spin structure of the nucleon(the fraction of the spin of the nucleon which is carried by the quarks). A nucleon's spin can be expressed as the sum of the quark spins, the quark orbital momentum, and the total angular momentum of the gluons. Inclusive DIS provides information about the total quark spin contribution to the nucleon and a limited amount information for the polarization of the sum of quarks and antiquarks. The reason is that the scattering cross section is proportional to the the square of the charge of the nucleon quark.
On the other hand, semi inclusive deep inelastic scattering experiments, where the hadrons in the final state are detected in coincidence with the scattered lepton, are sensitive to individual quark flavors. "The technique of detecting hadrons in the final state to isolate contributions to the nucleon spin by specific quark and antiquark flavors is called flavor tagging."<ref name="Airapetian2005"> A. Airapetian et al. (HERMES), Phys. Rev. D 71, 012003 (2005), hep-ex/0407032.</ref> "This exploitation of hadrons in SIDIS measurements requires knowledge of the probabilities of the various types of hadrons emerging from a struck quark of a given flavor . These probabilities are embodied in the fragmentation function, where and and are the energies in the target rest frame of the absorbed virtual photon (the struck quark) and the detected hadron." <ref>A. Airapetian et al. (HERMES) Phys. Rev. Lett. 92 012005(2004) </ref> In addition, it is known that at high values of the sea quarks(like (up antiquark)) do not have a major contribution in the nucleon.
The polarized quark distribution functions can be extracted from the SIDIS measurements using quark flavor tagging method excluding the assumptions used in inclusive DIS measurements. In SIDIS the double spin asymmetry can be expressed in terms of the cross sections of final state hadrons produced in the experiment<ref name="Airapetian2005"> A. Airapetian et al. (HERMES), Phys. Rev. D 71, 012003 (2005), hep-ex/0407032.</ref>:
where () represents the semi inclusive cross section of hadrons type which were produced in the final state when the spin of the initial electron beam was antiparallel(parallel) to the target nucleon spin. The semi-inclusive cross sections can be expressed in terms of the quark distribution functions and fragmentation functions:
The measured structure function in inclusive deep inelastic scattering experiments contains the contribution from all the different quark flavors to the total nucleon momentum and spin, without distinguishing the input from the individual quark flavors. Semi inclusive deep inelastic scattering experiments give us opportunity to determine the struck quark flavor, by detecting the hadron in the final state in coincidence with an electron.
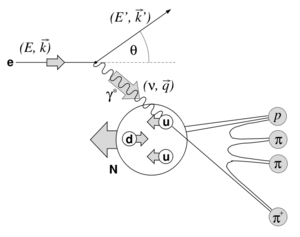
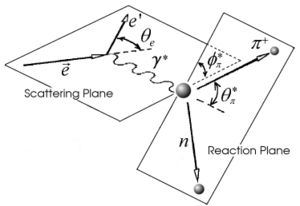
The kinematics of single pion electroproduction in SIDIS can be described by five variables: the virtual photon negative four-momentum transfered squared , W invariant mass of the photon-nucleon system, the polar and the azimuthal angle of the outgoing pion in center of mass frame and the scattered electron azimuthal angle. The incoming electron with four momentum is scattered of the target with four momentum , where M represents the rest mass of the target nucleon. The four momentums of the detected scattered electron and hadron are respectively and . Semi inclusive deep inelastic scattering is shown below on Figure. 1. The four momentum of the exchanged virtual photon, through which the SIDIS occurs, is the four momentum lost by the initial electron
The negative square of the four momenta can be written as , where is greater then zero. The energy transferred from the scattering electron to the target nucleon, which is also the energy of the virtual photon is given by
The Bjorken scaling variable x
The energy fraction of the virtual photon transferred to a hadron, which is detected in the final state in coincidence with the scattered electron is
where the last kinematical variable is the invariant mass of the scattering process available to produce the final hadronic state
Table 1. Kinematic variables in deep inelastic scattering
| Kinematic variable | Description |
|---|---|
| , | 4 - momenta of the initial and final state leptons |
| , | Polar and azimuthal angle of the scattered lepton |
| 4 - momentum of the initial target nucleon | |
| 4 - momentum of the virtual photon | |
| Negative squared 4 - momentum transfer | |
| Energy of the virtual photon | |
| Bjorken scaling variable | |
| Fractional energy of the virtual photon | |
| Squared invariant mass of the photon-nucleon system | |
| 4 - momentum of a hadron in the final state | |
| Fractional energy of the observed final state hadron |
The cross section for the electron scattering off the nucleon can be written as<ref>R. G. Roberts, The structure of the proton, Cambridge Monographs on Mathematical Physics, ISBN 0521351596, Cambridge University Press, 1990.</ref> :
and in the target rest frame it can be expressed in terms of the initial and final energies of electron and electron scattering angle :
where and are so called structure functions, and E the energy of the initial proton and electron. - the direction of the scattered electron. M is the mass of the target, in our case the proton.
As it was mentioned above, the DIS an interaction doesn't happen with the hadron as a whole, but with exactly one of its constituents. Each quark(constituent) carries the fraction four-momentum of the nucleon with probability density is the probability of finding the qth quark with fraction of the proton(neutron) four-momentum. Assuming all this, the structure functions can be written as sum of the elastic structure fractions weighted by . Taking into consideration that the mass of the ith quark is also the fraction of the nucleon mass :
and
DIS of the unpolarized electron by a nucleon can be described in terms of two so called structure functions and :
- and
The relation between the structure functions and can be obtained from the following equation:
where is the ratio of longitudinal to transverse deep inelastic scattering cross sections and . In the naive quark parton model the longitudinal transverse interference is neglected. In the Bjorken limit it can be reduced to the Callan-Gross relation:
"The structure function measures the parton density as function of x while describes the momentum density, both weighted with the coupling strength to the photon probe."[reference]
The distributions of up and down quarks in the nucleon are defined as u(x) and d(x). There are two categories of quarks: valence and sea quarks , assuming that . The constituent quark model (CQM and QPM) states that the proton(neutron) for example contains two up(down) quarks and one down(up) quark. So in the proton, summing over all the constituents should result in the following sum rule:
and
The electromagnetic structure function for proton and neutron can be expressed in terms of quark distribution functions:
can be obtained from by replacing u->d and vice versa.
From the last two equations the structure functions for proton and neutron can be written in terms of valence quark distribution functions:
and
For most of the fixed-target experiments, like EG1, the spin asymmetry is given by the ratio of the polarized structure function to the unpolarized: , where the polarized structure function is similar of the unpolarized structure function. The polarized structure function represents the helicity difference of quark number densities. As it is known the spin asymmetry and unpolarized structure function are measurable quantities and through them one can determine :
where is the quark distribution function with spin oriented parallel(antiparallel) to the spin of nucleon.
Independent from fragmentation function
The asymmetries from semi inclusive pion electroproduction using proton or deuteron targets can be written in terms of the difference of the yield from oppositely charged pions, a measurable quantity:<ref>E. Christova et al., hep-ph/9907265</ref>
rewrite sentences below
Assuming independent fragmentation, which states that the quark fragmentation into the hadrons is independent of the photon-quark scattering process or in other words the fragmentation process is independent of the initial quark environment, which starts the hadronisation process and using isospin and charge conjugation invariance for the fragmentation functions, i.e.
(Factorization Theorem: The quark fragmentation into the hadrons is independent of long distance effects and particularly of the final hadron identity.)
Eliminating strange quark contributions the polarized and unpolarized cross sections for pion electroproduction permits an expression in terms of valence quark distribution functions:
and unpolarized:
In the valence region where x_B>0.3, where sea quark contribution is minimized, the above asymmetries can be expressed in terms of polarized and unpolarized valence quark distributions:
The ratio of polarized to unpolarized valence up and down quark distributions may then be written as
and
The ratio of polarized to unpolarized valence quark distribution functions can be extracted using the last two equations.
- Fragmentation Function test
A complete test of independent fragmentation can be performed with polarized proton and neutron targets.
rewrite sentence below
An asymmetry we consider to be following :
The last expression of the asymmetry was obtained from the following equations:
and
"Independent fragmentation would hold if the measured asymmetry followed the x and behavior of the quantities and measured in deep inelastic scattering independent of z." <ref name="Forest">T. A. Forest, Measurement of Polarized Valence Quark Distribution Functions using Polarized Proton and Deuteron Targets with CLAS, 2000.</ref>
Experimental Setup
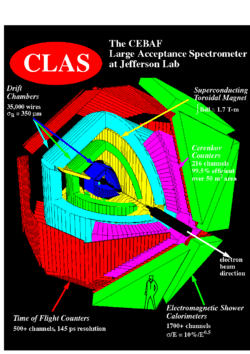
The CEBAF large acceptance spectrometer (CLAS) located in Jefferson Lab's Hall B was used to measure the final state particles resulting from the scattering of a polarized electron by a polarized nucleon. The CLAS uses six superconducting coils to establish a toroidal magnetic field along the incident electron's momentum direction. A set of three drift chambers are positioned to determine the trajectories of particles which pass through the 6 gaps between the magnet coils. The first drift chamber, Region 1 (R1), is placed at the entrance to the magnetic coil. A second chamber, Region 2 (R2), is placed in the center of the coils. The final chamber, Region 3 (R3), measures charged particle leaving the toroidal field. A total of 18 drift chambers are used to reconstruct the trajectory of charged particles passing through the magnetic field. After the drift chamber system, the CLAS detector is equiped with a Cherenkov counter for separating electrons from pions and with scintillators to determine the Time of Flight of a charged particle.
what is the sentence below suppose to say?
At the end of the detector the particle identification and timing(resolution) is achieved using electromagnetic calorimeters.
Five different targets were used during the experiment: , ,C12, liquid He-4 and frozen N15. The last three target were used to extract the contributions of the proton and deuteron from the other nucleons present when using the first two targets.
Target
- Target Materials
The EG1 experiment at Jefferson Lab used five different targets to measure polarized structure functions of the nucleon and perform background corrections. The main target materials for the experiment used frozen ammonia, , for the polarized protons and deuterated ammonia, for the polarized deuterons. A target ladder. placed 50 cm upstream of the standard CLAS target position, was used to position the desired target. The target ladder was designed and built by collaboration of the Italian Istituto di Fisica Nucleare, TJNAF, Oxford instruments and the University of Virginia. The solid targets(NH3 and ND3) were polarized using the method of Dynamic Nuclear Polarization(DNP). <ref name="Prok2004">Y. Prok, Ph.D Thesis, University of Virginia (2004).</ref> Three other targets, C12, liquid He-4 and frozen N15 were used to remove the Nitrogen and Helium background from NH3 and ND3 target data. Helium is used to cool the ammonia targets
Ammonia targets were selected because of their ability to produce high polarization and they are less effected by beam radiation. On the other hand, the damage caused by this radiation can be repaired by annealing. The target is warmed up to liguid nitrogen temperature for annealing. In addition, the ammonia target has a high ratio of free nucleons (~3/18) approximately 16.5 % for and 26.6 % for . One disadvantage of choosing ammonia is the polarization background caused by 15N(spin - 1/2), or 14N(spin - 1), which was accounted for by taking data using a solid N-15 target.<ref name="Chen">S. Chen, Ph.D Thesis, The Florida State Universuty (2006)</ref>
- Target Magnet
A 5 T magnetic field is established using a produced pair of superconducting Helmholtz coils oriented such that the magnetic field is parallel to the beam direction. The field induces the hyperfine splittings needed to polarize the target material using 140 Ghz RF waves. The uniformity of the field is varying less than over a cylindrical volume of 20 mm in diameter and length. This configuration is necessary for DNP. The particles with scattering angles between 0-50 degrees are detected in the CLAS as well as 75-105 degrees. The Helmholtz coils block particles scattering between 50 and 75 degrees. The target magnetic field does not interact with the electron beam, however it is effective in shielding the drift chambers from low energy Moller electrons. The target field bends the scattered particles in the azimuthal direction and it falls rapidly with distance as (). The effect of the magnetic field on the drift chambers is negligible.<ref name="Chen">S. Chen, Ph.D Thesis, The Florida State University (2006)</ref>
The CEBAF Large Acceptance spectrometer
- The Torus Magnet
The torus magnet for CLAS detector consists the six superconducting coils located around the beam line in a toroidal geometry, producing the magnetic field in the direction. Each magnetic coil defines the sector of detector. So the CLAS detector has six sectors(spectrometer). The system of the magnet is defined in spherical coordinates where the z-axis are along the beam direction and the x and y axis along the horizontal and vertical plane normal to the beam line.
The maximum current for the CLAS magnet is 2860 A, in the forward direction the total magnetic field is 2.5 T-m and at a polar scattering angle with 90 degrees 0.6 T. The magnet itself is around 5 m in diameter and 5 m in length. The coils of the magnet are cooled by liquid helium circulating through cooling tubes to a superconducting temperature of 4.5 K.<ref name="Prok2004">Y. Prok, Ph.D Thesis, University of Virginia (2004).</ref> One can find out the charged particles momentum knowing the trajectory of a particle. In Eg1b experiment, the operated torus values were: 2250, -2250, 1500, -1500.
- Drift Chambers
In order to track the charged particles in the EG1b experiment a drift chamber system is used. A drift chamber is a particle tracking detector that measures the drift time of ionization electrons in a gas to calculate the spacial position of an ionizing particle.
The electric field in a drift chamber is produced by the anode(sense wire) and cathode(field wire) wires. The charge particle traveling trough the drift chamber ionizes the gas, producing the electrons that drift to the anodes. After time(drift time) electrons are collected at the anode(sense wire) generating the pulse at t time. The distance from the traversing particle to the sense wire can be calculated using the drift time and velocity.
The drift chamber system in CLAS detector is divided into three regions, each consisting six separate chambers(six sectors). Region 1 (R1) chambers are placed closest to the target, where the magnetic filed is low. Region 2 (R2) chambers are in a high magnetic field region, they are located between the magnetic coils. Region 3 (R3) chambers are outside the torus coils and they are largest ones. The drift chambers contain three type of wires stretched between the endplates: sense, guard and field. The endplates are attached to the drift chamber so that the angle they form is equal to 60 degrees. Each drift chamber is subdivided into two separate superlayers. Each superlayer with six layers of drift cells, and each drift cell with one sense wire surrounded by six field wires forming a hexagonal shape. Each superlayer is surrounded by guard wires at a positive potential to stimulate the electric field caused by the drift cells. The sense wire is operated at positive potential and the field wire at negative. In each superlayer the distance between the sense and field wire increases with the radial distance from the target. In R1 the average distance between the sense and field is 0.7 cm, in R2 1.15 cm and in R3 2.0 cm.<ref>M. D. Mestayer, et. al., The CLAS drift chamber system, NIM A 449 (2000) 81.</ref>
The gas used to fill the CLAS drift chamber is a 90 - 10 % mixture of the argon(Ar) and , where Ar has an ionization gain of . Inside the drift chamber the constant pressure is provided by outflowing the gas. The chamber endplates are equipped with the circuit board with a single channel differential pre-amplifier for each sense wire.
- Cherenkov detector
The threshold CLAS Cherenkov detector is used to distinguish electrons from pions. The mixture gas used to fill the Cherenkov counter is perfluorobutane gas at atmospheric pressure. The advantage of Perfluorobutane gas is its high index of refraction n=1.00153, which results in a high photon yield and the following energy thresholds. The threshold for the Cerenkov radiation can be written as , or for energies , where v is the velocity of charged particle, n index of refraction for the medium, c speed of light and . In our case , accordingly one can calculate the energy threshold for different charged particles, for electrons it is 9 MeV and for pions 2.5 GeV. The Cherenkov detector was designed to maximize the coverage in each of the sectors up to an angle degrees.<ref>G. Adams, V.Burkert, et. al., The CLAS Cerenkov Detector, NIM A 465 (2001) 414-427 </ref>
As a light collector were used the system of mirrors , the light collecting cones and photomultiplier tubes(PMTs). In the extreme regions of the angular acceptance of the spectrometer the number of detected photoelectrons is too low. To get acceptable efficiency of the detector in these regions photomultiplier tubes were placed. The calibration of the Cherenkov detector is in terms of the collected number of photoelectrons.
- Scintillators
The CEBAF Large Acceptance Spectrometer (CLAS) is equipped with 288 scintillator counters. The purpose of the scintillator is to determine the time of flight for the charged particles and to trigger it in coincidence with another detector system for the particle identification. The time of flight system is built so that time resolution at small polar angles ps and at angles above 90 degrees ps. This time resolution helps to discriminate pions and kaons up to 2 GeV/c.
The time of flight system is located between the Cherenkov detectors and electromagnetic calorimeters. The scintillator strips(BC_408) are located perpendicularly to the average particle trajectory with an angular polar coverage of 1.5 degrees. Each sector of The CLAS detector consists of 48 scintillator strips with a thickness of 5.08 cm. The length of the scintillators varies from 30 cm to 450 cm and the width is between 15 cm at small polar angles and 22 cm for the large angles.
- Calorimeter
The CLAS detector contains 8 modules of electromagnetic calorimeter. A calorimeter is a device that measures the total energy deposited by a crossing particle. They are useful in detecting neutral particles and distinguishing between electrons and hadrons due to their different mechanism of depositing energy. The CLAS calorimeter has three main functions:
1) detection of electrons at energies above 0.5 GeV;
2) detection of photons with energies higher than 0.2 GeV;
3) detection of neutrons, with discrimination between photon and neutrons using time-of-flight technique.
6 calorimeter modules of the CLAS detector are placed in each sector in the forward region (polar angle of 10-45 degrees, forward angle calorimeter), while the other two modules are located at large angles in sectors 1 and 2(50-70 degrees, large angle calorimeter). The forward calorimeter has a lead/scintillator thickness ratio 0.2, with 40 cm of scintillators and 8 cm of lead per module. The lead-scintillator sandwich is shaped as a equlaterial triangle in order to match the hexagonal geometry of the CLAS detector. It is made of 39 layers of a 10 mm BC_412 scintillator and lead sheet of thickness of 2.2 mm. Each scintillator layer contains 36 strips parallel to one side of the triangle, with this configuration each orientation is rotated by 120 degrees from another one. This gives three views each containing 13 layers providing stereo information of the location of the energy deposition.
To improve hadron identification, there was provided longitudinal sampling of the shower. Each set of 13 layers were subdivided into an inner 5 layers and outer 8 layers stack.
Experiment running conditions
| Beam Energy | Torus Current | Begin Run | End Run | file used | # trig() | expected # evts() | Target |
|---|---|---|---|---|---|---|---|
| 5627 | 2250 | 27356 | 27364 | dst27358_02.B00 | 56 | 19.4 | 12C |
| 5627 | -2250 | 27366 | 27380 | dst27368_02.B00 | 130 | 13.6 | 15N |
| 5627 | 2250 | 27386 | 27499 | dst27388_02.B00 | 1210 | 20.2 | NH3 |
| 5735 | -2250 | 26874 | 27068 | dst26904_02.B00 | 1709 | 19.9 | 12C |
| 5735 | 2250 | 27069 | 27198 | dst27070_02.B00 | 31509 | 15 | MT |
| 5764 | -2250 | 26468 | 26722 | dst26489_02.B00 | 1189 | 10 | NH3 |
| 5764 | -2250 | 26776 | 26851 | dst26779_02.B00 | 662 | 15.9 | NH3 |
Table 2. Experimental running conditions.<ref>http://www.jlab.org/Hall-B/secure/eg1/EG2000/fersch/QUALITY_CHECKS/file_quality/runinfo.txt</ref>
Preliminary Results
The differential cross-section and electron beam asymmetries were measured using the CEBAF Large Acceptance spectrometer (CLAS) at Thomas Jefferson National Lab with a 5.7 GeV continues electron beam of luminosity and polarized target(frozen ammonia) and compared to the E99-107 data.
The kinematics of single pion electroproduction can be described by five variables: the virtual photon negative four-momentum transfered squared , W invariant mass of the photon-nucleon system, the polar and the azimuthal angle of the outgoing pion in center of mass frame and the scattered electron azimuthal angle. <ref name="Park2008" >K. Park, V. D. Burkert, W. Kim, (The CLAS Collaboration), Phys. Rev. C 77, 015208 (2008). arXiv:0709.1946v2 [nucl-ex] </ref>
The five-fold differential cross section can be written in the following way for a single pion electroproduction:
where represents the efficiency of the cherenkov detector, - the integrated luminosity, is the acceptance factor and the Jacobian term can be expressed in terms of the initial and final energy of lepton:
- Cuts
In the semi-inclusive asymmetry analysis scattered electrons are used. The contamination in the electron sample is removed using the cuts on the energy deposited in the electromagnetic calorimeter, the number of photoelectrons in the Cherenkov counter and fiducial cuts.
The energy deposition in the calorimeter for electrons and pions is different. Pions are minimum ionizing charge particles and energy deposited into the calorimeter, independent of the particles momentum is constant. It is approximately ~ 0.08 GeV. On the other hand, electrons produce photoelectrons and create electromagnetic shower releasing the energy into the calorimeter which is proportional to their momentum. In order to remove contamination due to the energy deposition in the calorimeter the following cut was introduced: . The cut was also applied to the energy collected in the inner part of the calorimeter: , because the ratio of the energy deposited in the total to the inner calorimeter depends on the thickness of the detector and is a constant.
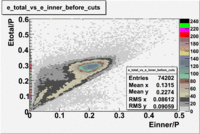
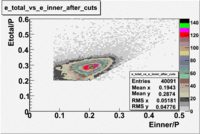
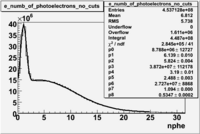
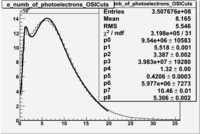
In addition to the cut on the energy deposited into the electromagnetic calorimeter, the misidentified electrons were excluded requiring a signal in the threshold CLAS Cherenkov detector, which is used to distinguish electrons from pions up to 2.5 GeV momentum of the particle. The energy threshold for electrons in the Cherenkov counter is 9 MeV and for pions 2.5 GeV. There are no many pions above 2.5 GeV momentum. A bad recollection of the cherenkov light that occurs for a particular kinematics is responsible for a faulty peak around ~1.5 on the number of photoelectons distribution shown below. To eliminate the faulty peak and high energy pions, which have enough energy to produce photons the geometrical cuts were applied on the data. The second histogram below shows that after cuts the peak around 1.5 disappears.
| No cuts | OSI Cuts |
Because of wide range of kinematics, was measured only for certain lepton scattering angle and W invariant mass. Applying above described cuts: EC_inner>0.06, EC_tot/p>0.2, nphe>2.5 and , for he following invariant mass and the vs relative rate distribution is shown below on the graph and compared with E99-107 data, which by itself is in agreement with the models.
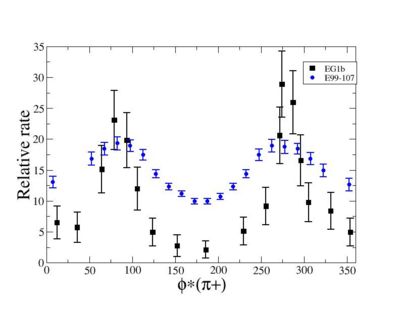 vs Relative rate for fixed and <ref name="Park2008" > Bogus text</ref> <ref> http://clasweb.jlab.org/cgi-bin/clasdb/msm.cgi?eid=14&mid=16&data=on </ref> |
The EG1b data for kinematics chosen above show the same shape as E99-107 data.
Future Plans
Data analyzed above was for unpolarized beam, we are planning to analyze data for double polarized experiments. Future goals are to plot the double spin asymmetry and the ratio of polarized valence quark distribution function to unpolarized.
Notes
<references/>