HRRL Simulations

This document describes the simulations performed to estimate the radiological background in the event that a 1 nA electron current from the HRRL enters the experimental cell.

Radiation monitors: Ludlum Model 45-8.

Low energy gamma cutoff = 60 keV

Tungsten SImulation

I created a world volume filled with Air to represent the experimental cell.

I created a 2mm thick tungsten target that is 30 cm x 30 cm in area.

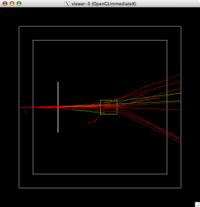
The image below shows several electrons hitting the tungsten foil, then scattering in air. The red lines are electrons and the green ones are photons.

Run 1

I then ran 1 million events in which an incident 7 MeV electron hit the 2 mm thick Tungsten with the physics processes

    if (particleName == "gamma") {
     // gamma         
   pmanager->AddDiscreteProcess(new G4PhotoElectricEffect);
     pmanager->AddDiscreteProcess(new G4ComptonScattering);
     pmanager->AddDiscreteProcess(new G4GammaConversion);
     
   } else if (particleName == "e-") {
     //electron
     pmanager->AddProcess(new G4MultipleScattering,-1, 1,1);
     pmanager->AddProcess(new G4eIonisation,       -1, 2,2);
     pmanager->AddProcess(new G4eBremsstrahlung,   -1, 3,3);      

I only kept event in which had a momentum component towards the ceiling

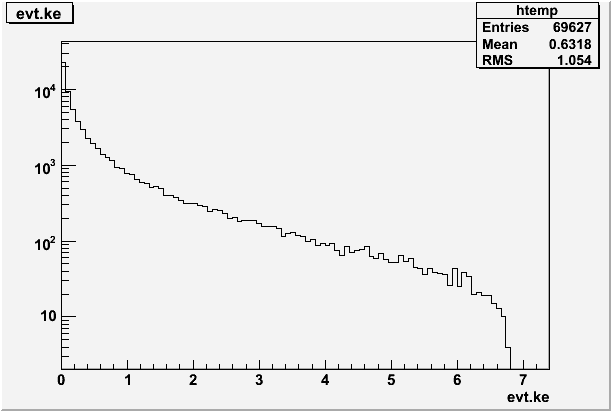
The energy distribution (in MeV) of the gammas headed towards the roof is shown below. Of the 1 million electrons incident on the 2 mm thick Tungsten target, only 70,000 gammas were headed towards the cieling. This does not mean that they hit it, they could have hit the wall.

If I sum the above distribution I see a total energy of 43,987 MeV going up from the 1 million 7 MeV electrons hitting the 2mm Tungsten target.

1 Rad =[math]\frac{J}{100 kg}[/math] = the amount of energy absorbed per 100 kg of material

To calculate the worst possible case lets assume all of the radiation is absorbed by a person (there is no concrete ceiling).

Converting the energy from MeV to Joules

[math]4.4 \times 10^4 MeV \times \frac{1.6 \times 10^{-19} J }{10^{-6} MeV} = 4.4 \times 10^{-9} J[/math]

In terms of the energy per beam current charge we would have

[math]\frac{4.4 \times 10^{-9} J}{10^6 e^-} \times \frac{1 e^-}{1.6 \times 10^{-19} C} = \frac {44 krad}{C}[/math]

I we ran the HRRL for 1 hour at the maximum beam current of 80 mA per 100 ns pulse and 1 kHz rep rate then the dose to the ceiling would be

[math]80 mA \times 100 ns = 8 \times 10^{-9} Coul \times \frac{1000 pulses}{sec} \times \frac{3600 sec}{hr} = 0.0288 Coul/hr \times \frac {44 krad}{C} = 1.4 kRad/hr[/math]

The total photon radiation hitting the upper half of the experimental cell is predicted to be 1.4 krad/hr. To determine the dose on a radiation detector you just need to scale by the solid angle.

Go back