R3DC Report 2-08
Introduction
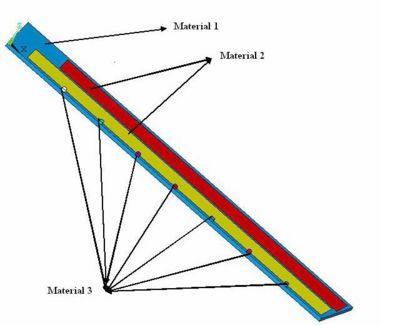
R3 Description
Geometry
Material Specifications
Specific part Drawings
Endplate Deflection
Point Load Deflection
A simple calculation based on the definition of Young's modulus can yield an order of magnitude level estimate for the deflection of an endplate made from Aluminum. According to the definition of Young's modulus
where
- Young's Modulus for Aluminum
- point force/load
- width of the endplate
- deflection of endplate due to point force
- length of the endplate
- thickness of the endplate
A deflection of 6 mm is expected for a 5 cm thick Aluminum endplate, after solving the above equation for and inserting the given values. If a 5 cm thick stainless steel endplate were used, the deflection would drop from 6 mm to 2 mm. The amount of deflection does not substantially decrease when stainless steel is used despite its larger Young's Modulus. The cubic dependence of the deflection on the thickness of the endplate is used to reach the minimum endplate deflection criteria of 50 \ instead of using stiffer material. Composite materials were considered in order to increase the thickness of the material without substantially increasing the weight of the endplate.
| Material | Youngs Modulus | Density |
| MPa | ||
| Polyeurethane Foam FR-3700 | 140 | 240 |
| Hexacell with holes | ||
| Carbon Fiber Rods | 210 | 580 |
Distributed Load Deflection
Distributed load FEA
Carbon Rod Buckling
Compression
Buckling Load Threshold
Buckling FEA
=3-D Analysis