Analysis

EG1 run database
run summary
polarization info

Particle Identification

Electron

Cuts

Calorimeter based cuts

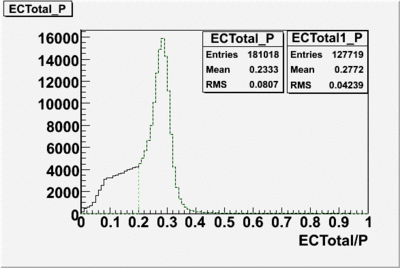
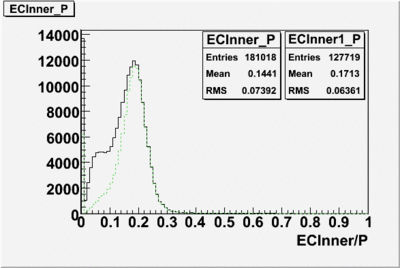
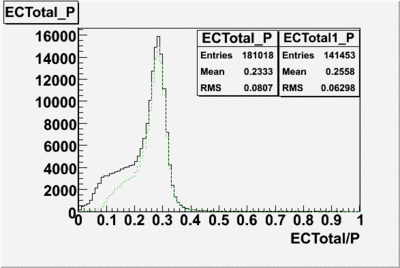
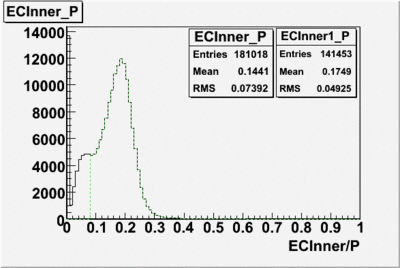
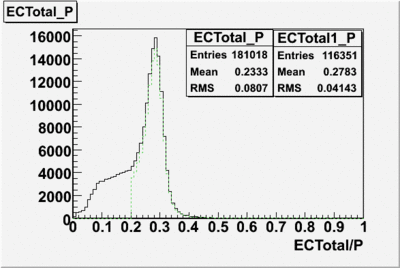
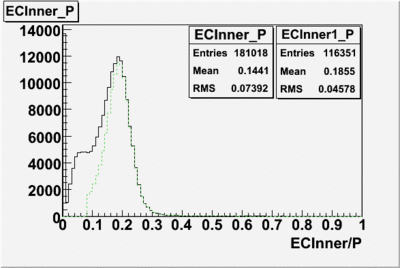
The distributions below represent two types of cuts applied to improve the electron particle identification (PID) using a 4 GeV electron beam incident on an NH3 target. The electron calorimeter is segmented into an inner[math]EC_{inner}[/math] and an outer[math]EC_{outer}[/math] region. The total energy absorbed by the calorimeter system is recorded in the variable [math]EC_{tot}[/math]. The momentum ([math]P[/math]) is calculated using the reconstructed track and the known torus magnetic field. The distributions of [math]EC_{tot}[/math] and [math]EC_{inner}[/math] are shown below where both have been divided by the electron momentum and no cuts have been applied.

[math]EC_{tot}\gt 0.2*p[/math]

Without any cuts we have 181018 entries. After using the following cut [math]EC_{tot}\gt 0.2*p[/math] we are getting 127719 entries, which is about 70.55% of 181018.

[math]EC_{inner}\gt 0.08*p[/math]

After the cut on the energy deposited into inner part of electron calorimeter, number of entries decreases by 22%.

Both cuts [math] EC_{tot}\gt 0.2*p [/math] and [math] EC_{inner}\gt 0.08*p [/math]

In case of using the cuts of the total deposited energy and the energy deposited into inner calorimeter number of entries decreases ~36%

summary table

Beam Energy	Torus Current	Begin Run	End Run	file used	cuts			num trig	expected # evts
					[math]EC_{tot}\gt 0.2*p[/math]	[math]EC_{inner}\gt 0.08*p[/math]	[math]EC_{tot}\gt 0.2*p [/math] and [math] EC_{inner}\gt 0.08*p[/math]
1606	1500	25488	25559	dst25504_02.B00	64%	49.5%	78%
1606	1946	25560	25605
1606	1500	25669	25732	dst25669_02.B00	64%	49%	78%
1606	1500	25742	26221	dst25754_02.B00	21%	11%	24%
1606	-1500	26222	26359	dst26224_02.B00	4.6%	3%	6.6%
1724	-1500	27644	27798	dst27649_02.B00	4.8%	2.2%	5.9%
1724	1500	28512	28526
1724	-1500	28527	28532
2288	1500	27205	27351	dst27225_02.B00	20.2%	13%	25.6%
2562	-1500	27799	27924	dst27809_02.B00	5.7%	4.6%	8.6%
2562	-1500	27942	27995	dst27942_02.B00	6.1%	4.4%	8.9%
2562	1500	28001	28069	dst28002_02.B00	27.8%	13%	29.6%
2792	-1500	27936	27941	dst27937_02.B00	6.7%	5%	9.9%
3210	-2250	28549	28570
4239	2250	28074	28277	dst28075_02.B00	35.3%	23.9%	40.5%
4239	-2250	28280	28479	dst28281_02.B00	9.1%	9.4%	13.6%
4239	2250	28482	28494
4239	-2250	28500	28505
4239	2250	28506	28510	dst28509_02.B00	29.5%	22%	36%
5627	2250	27356	27364	dst27358_02.B00	33.2%	27.8%	41.3%
5627	-2250	27366	27380	dst27368_02.B00	12.6%	14.8%	19.5%
5627	2250	27386	27499	dst27388_02.B00	33.4%	27.8%	41.4%
5627	965	27502	27617
5735	-2250	26874	27068	dst26904_02.B00	13%	15%	20%
5735	2250	27069	27198	dst27070_02.B00	33.3%	28.8%	42.2%
5764	-2250	26468	26722	dst26489_02.B00	12.2%	14.4%	19.1%
5764	0	26723	26775
5764	-2250	26776	26851	dst26779_02.B00	13.5%	15.5%	20.5%

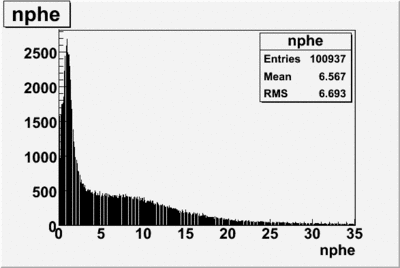
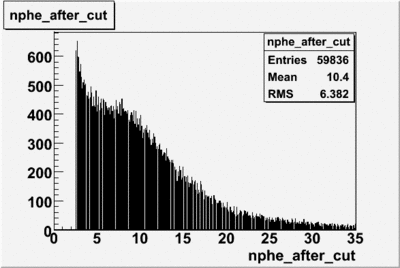
Cut on the number of photoelectrons

In this case is used a cut on the number of photoelectrons, which is [math]nphe\gt 2.5[/math]. The plots below show the effect of the number of photoelectrons cuts on the Cerenkov distribution. We see that after using cut the number of entries decreases ~40.7%