VanWasshenova_Thesis#Mlr_Summ_TF
Moller Summary
Scattering Xsect
https://wiki.iac.isu.edu/index.php/Converting_to_barns
[math]\frac{d\sigma}{d\Omega}=\frac{ e^4 }{8E^2}\left \{\frac{1+cos^4\frac{\theta}{2}}{sin^4\frac{\theta}{2}}+\frac{1+sin^4\frac{\theta}{2}}{cos^4\frac{\theta}{2}}+\frac{2}{sin^2\frac{\theta}{2}cos^2\frac{\theta}{2}} \right \}[/math]
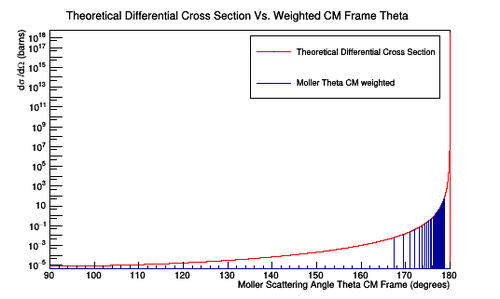 Figure 3a: A plot of the number of Moller scattering angle theta in the center of mass frame versus the theoretical differential cross section. The width of the bins is 0.001 degrees for the angles in the center of mass frame corresponding to angles of 5 to 40 degrees in the lab frame. A weight has been assigned for each value in theta which will give the theoretical differential cross section when applied. |
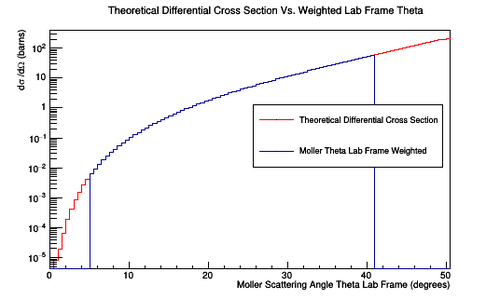 Figure 3b: A plot of the number of Moller scattering angle theta in the lab frame versus the theoretical differential cross section. The width of the bins is 0.5 degrees for the angles in the lab frame. A weight has been assigned for each value in theta which will give the theoretical differential cross section when applied. |
Weight the E-vs-Theta plot with Xsect
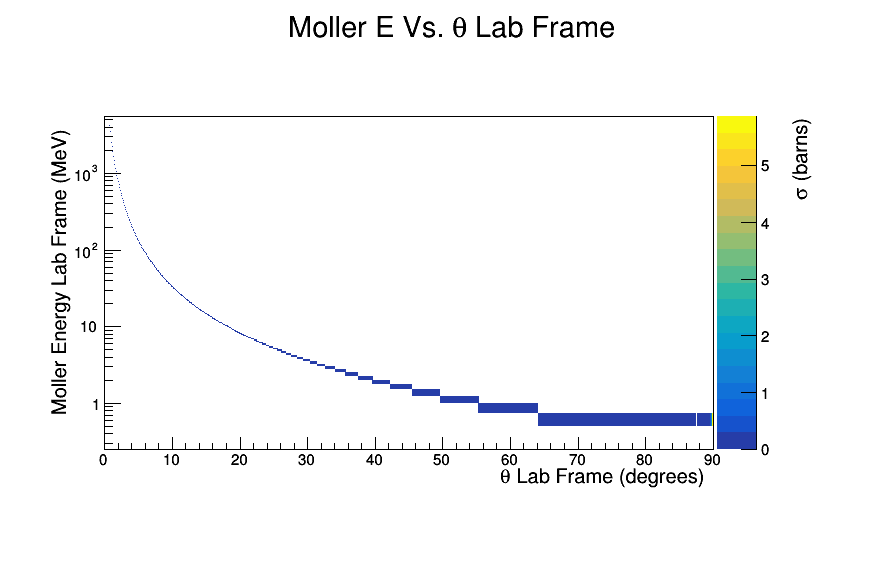
Figure 2: Using the theoretical differential cross section, the distribution of Moller electrons for a CM energy of approximately 53Mev can be distributed through the CM scattering angle Theta. Using Lorentz transformations, these distributions can be transformed to the lab frame. At around 60 degrees in the lab the Moller electron has an energy of close to 1 MeV. Such a low energy does not allow the Moller electron to leave the constrains of the target where they are created.
Baseline
Moller events using an lH2 target geometry No Raster
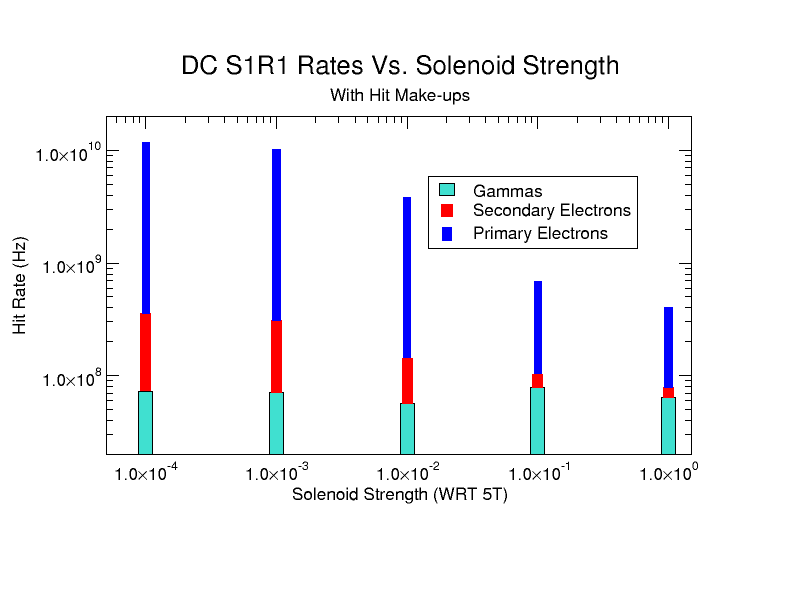
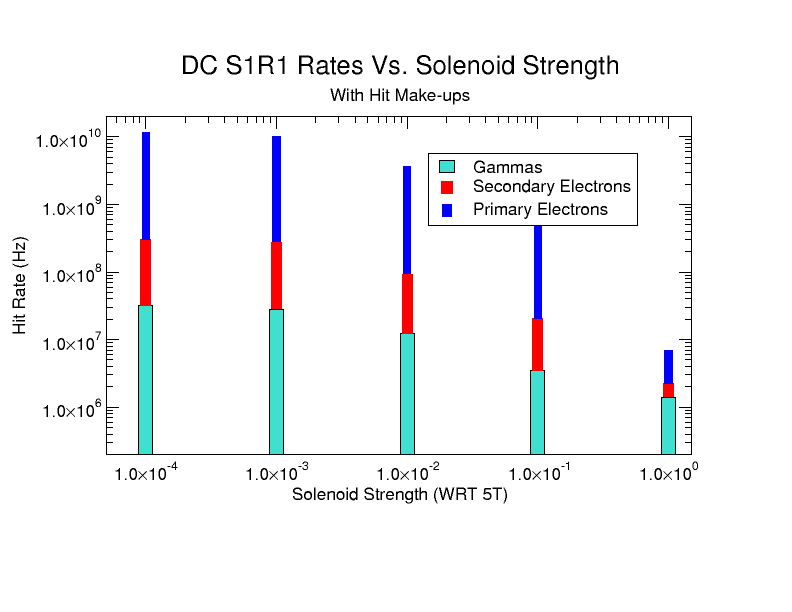
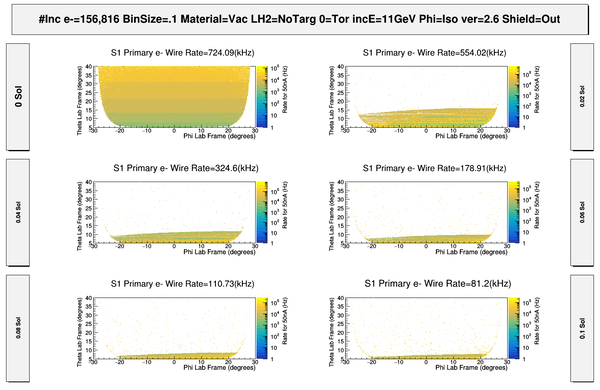
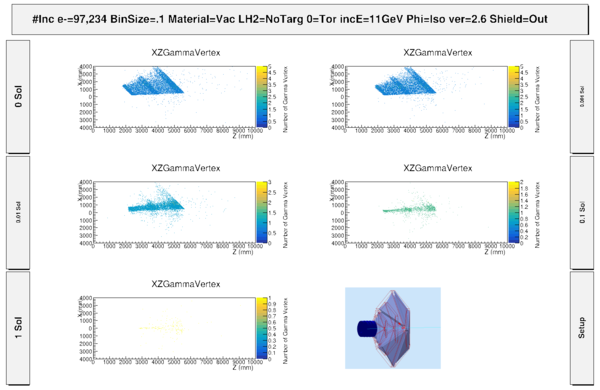
DC hits -vs- Solenoid
Starting the clas12 Moller simulation with a simple configuration, most components downstream with respect to the drift chambers are taken out of the gcard file. The remaining components, the Drift Chamber (DC), the Solenoid, and the Magnetic Components (CAD) are all that remain as shown below. The Torus field is held at zero Tesla, and the Solenoid field strength is increased from 0 to it's max of 5T.
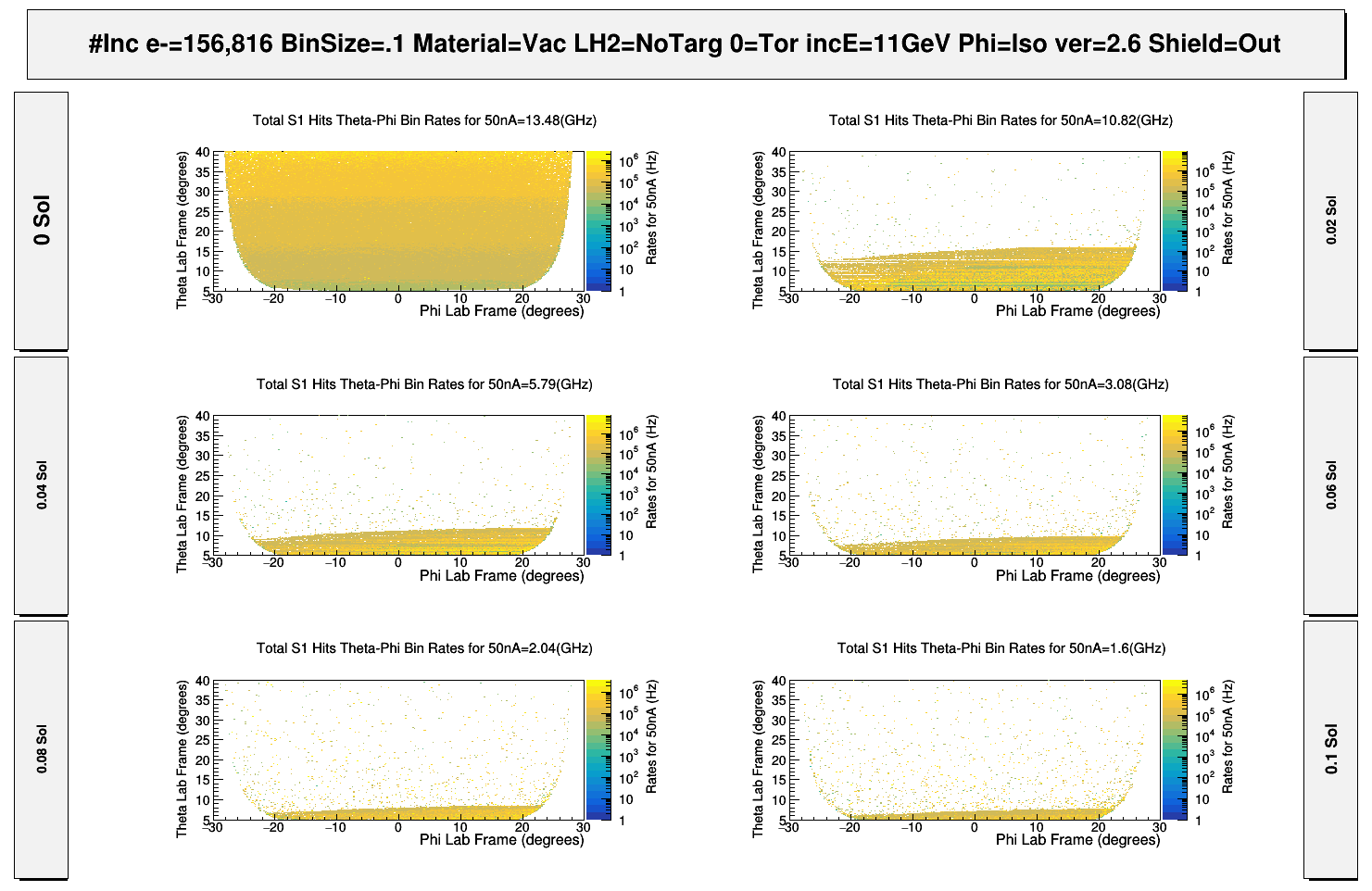
Figure 2: With the Torus strength at zero Telsa, the solenoid is varied to show the hits within the DC moving off the faces of R1. These hits consist of primary Moller electrons, as well as secondary electrons and photons created by the Moller electrons.
As the Solenoid field strength increases, the Moller electrons are forced to into a helical path of decreasing radius, effectively "rotating" off the DC face. However, as the field reaches maximum, there are still particles which are found at higher values of [math]/theta[/math] that would have been expected to have remained after the effects of the Solenoid.
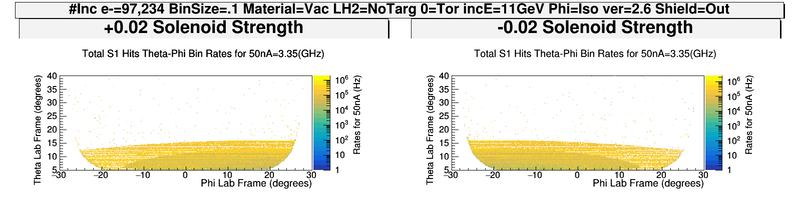
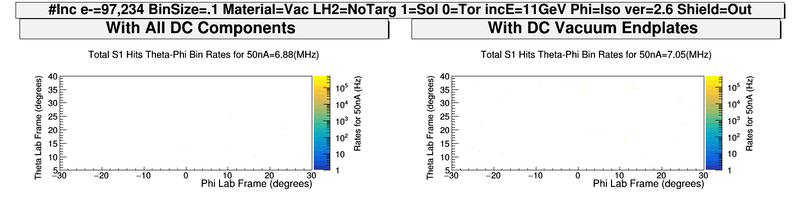
Without Magnet Components
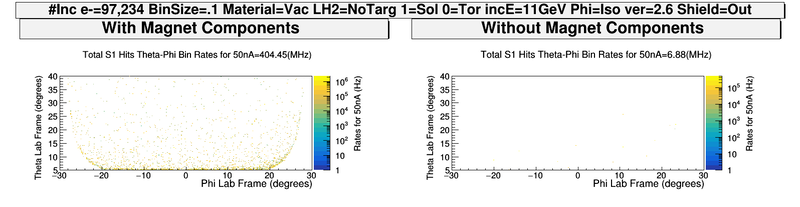
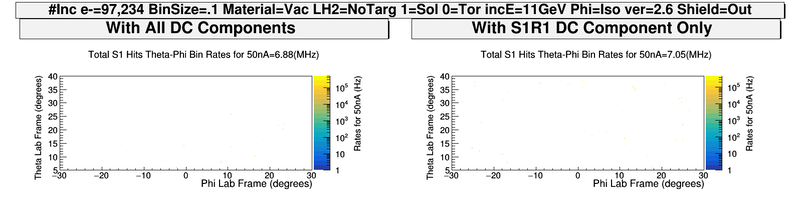
With Only S1R1 DC
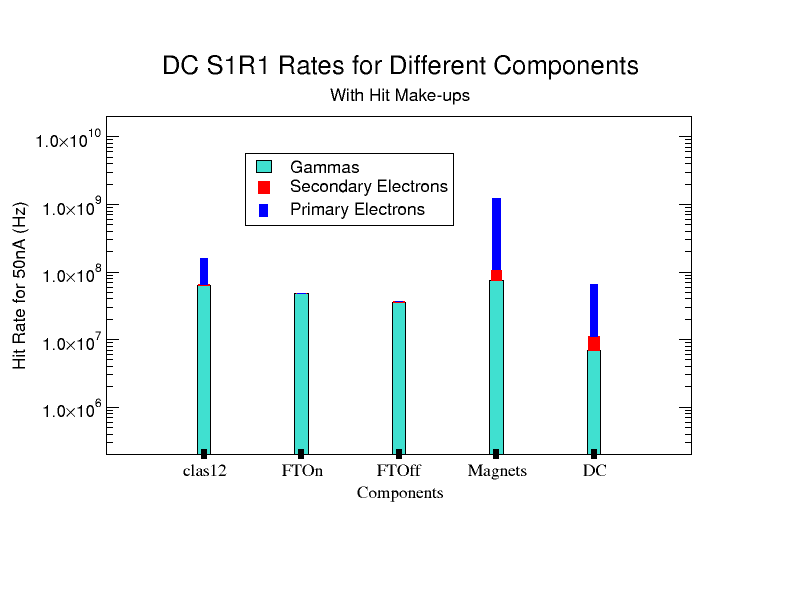
What are the particles in the R1S1 only plot and where are they from
Moller Electron Events(1st hits)
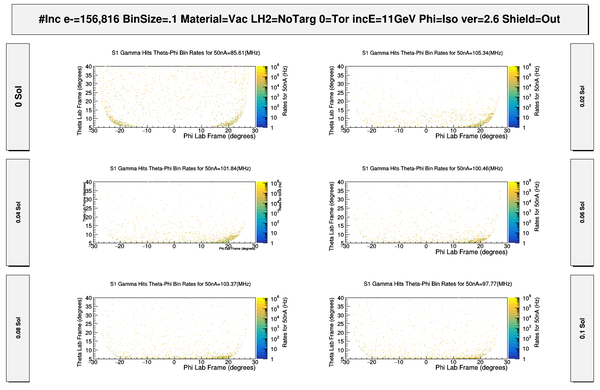
Photons Hits in R1
Tomography
Moller events using an dual polarized target geometry with Raster
Photon Hits in R1 when Raster size has radius of 0.2 cm
Moller rate -vs- length of a single taerget
0.5 cm radius -vs- Z
Target is a one 0.5 cm radius cylinder of length Z.
By how much does the moller rate change at full field ?
Latest Stuff
VanWasshenova_Thesis#Mlr_Summ_TF













