Mlr Summ TF
Revision as of 20:12, 30 August 2018 by Vanwdani (talk | contribs) (→Moller events using an lH2 target geometry No Raster)
VanWasshenova_Thesis#Mlr_Summ_TF
Moller Summary
Scattering Xsect
https://wiki.iac.isu.edu/index.php/Converting_to_barns
Weight the E-vs-Theta plot with Xsect
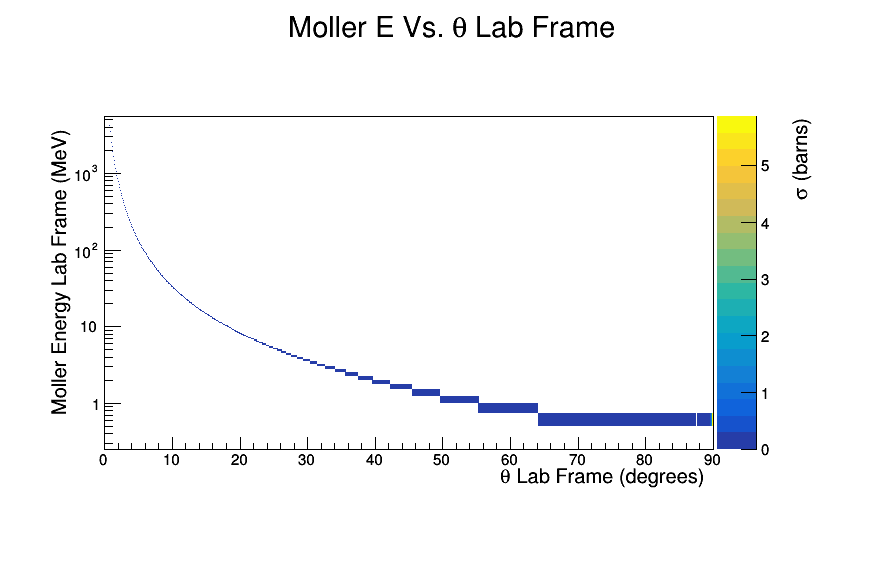
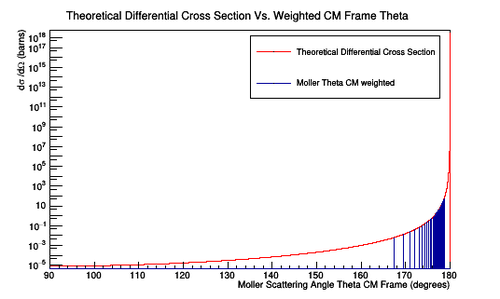
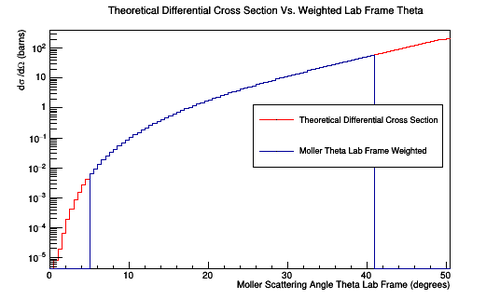
Figure 2: Using the theoretical differential cross section, the distribution of Moller electrons for a CM energy of approximately 53Mev can be distributed through the CM scattering angle Theta. Using Lorentz transformations, these distributions can be transformed to the lab frame. At around 60 degrees in the lab the Moller electron has an energy of close to 1 MeV. Such a low energy does not allow the Moller electron to leave the constrains of the target where they are created.
Baseline
Moller events using an lH2 target geometry No Raster
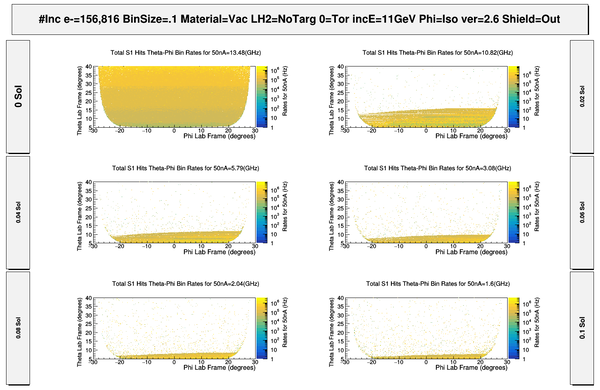
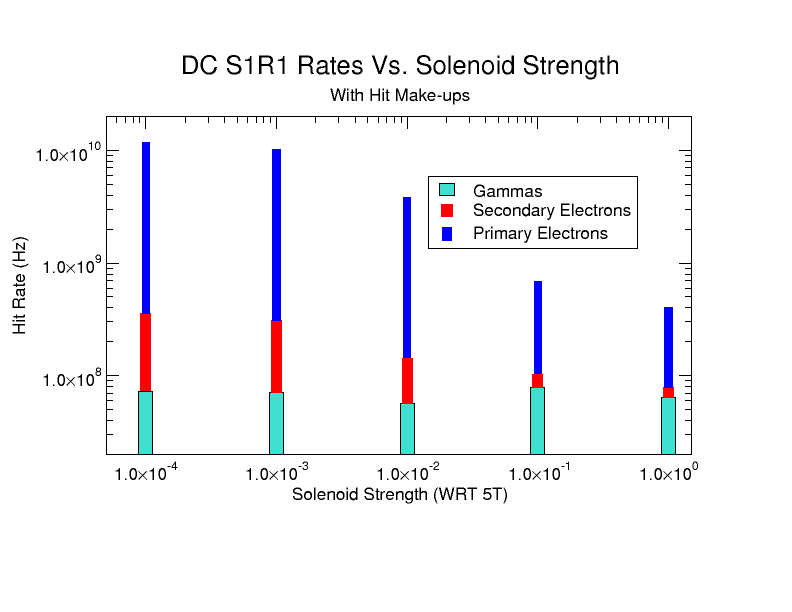
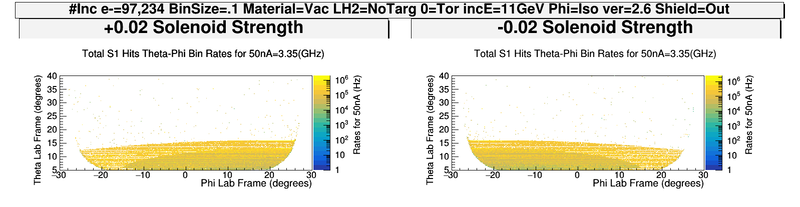
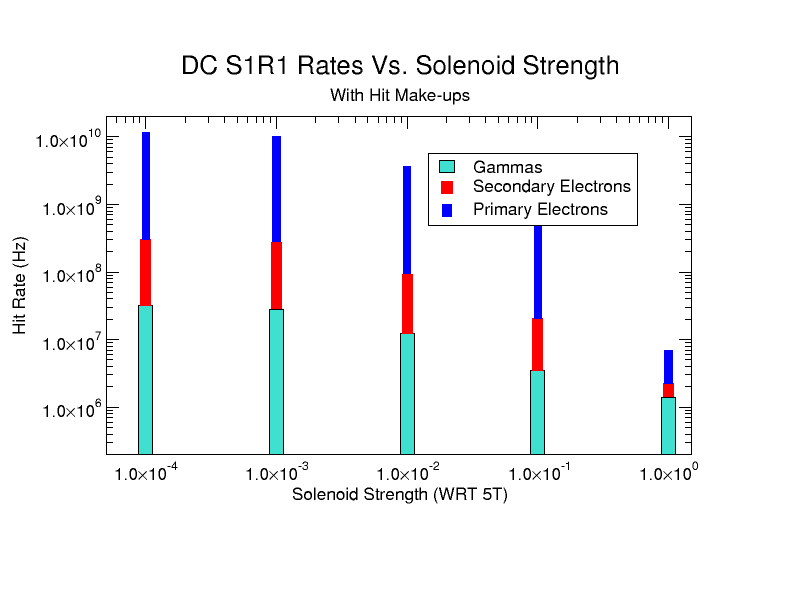
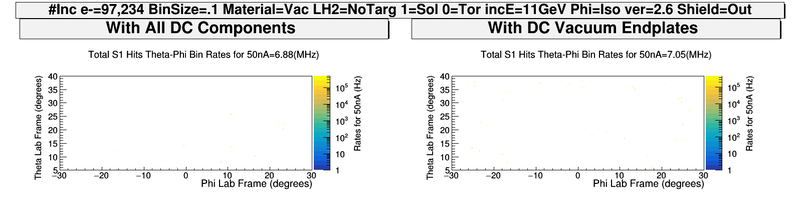
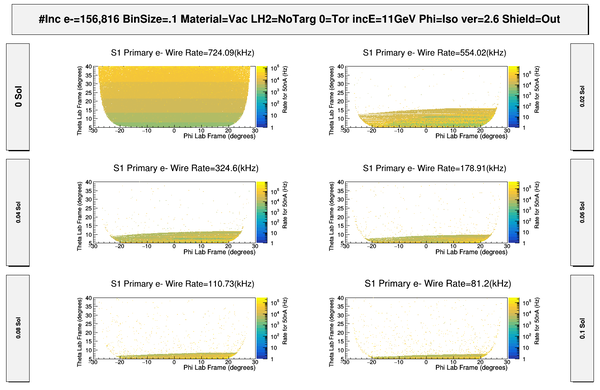
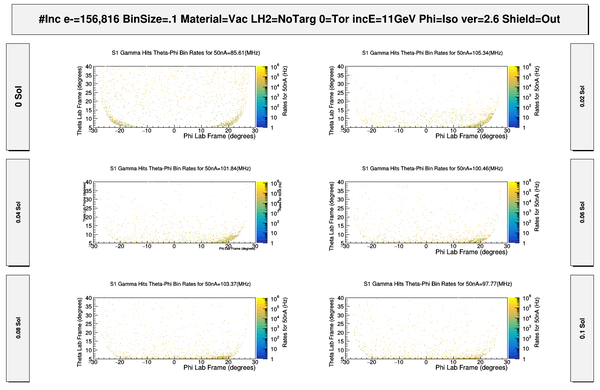
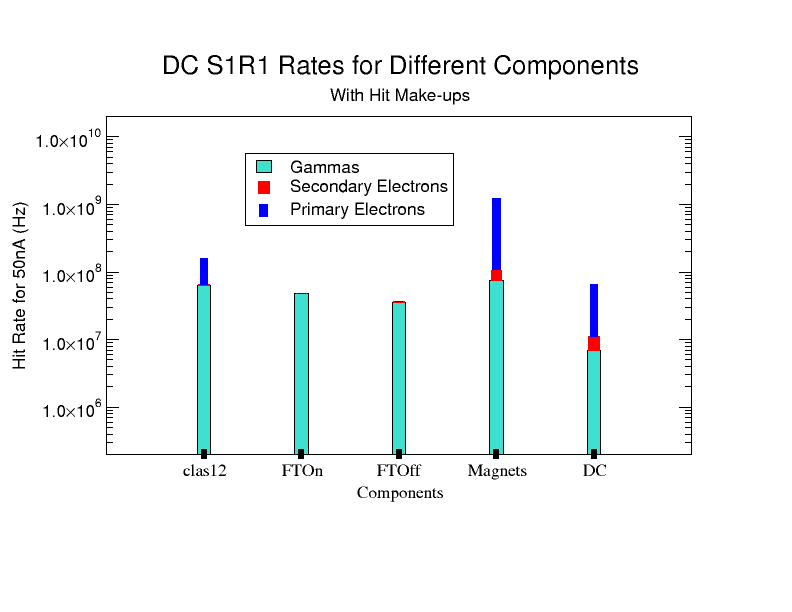
DC hits -vs- Solenoid
With the Torus at zero Magnetic field the solenoid is changes to show how moller electrons move off the faces of R1 DC.
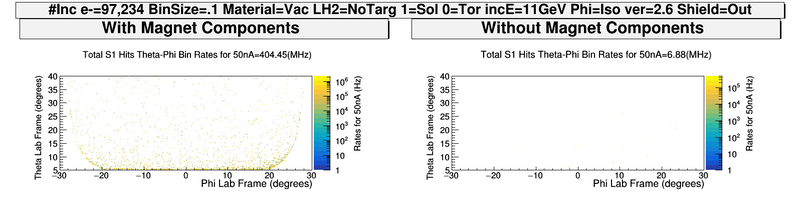
With Magnet Components
Without Magnet Components
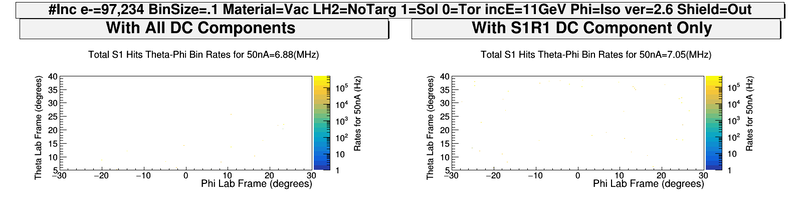
With Only S1R1 DC
What are the particles in the R1S1 only plot and where are they from
Moller Electron Events(1st hits)
Photons Hits in R1
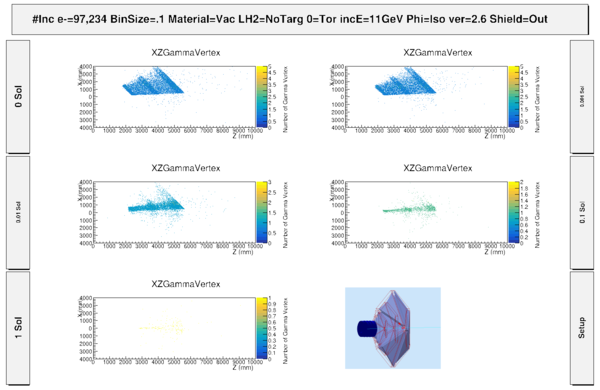
Tomography
Moller events using an dual polarized target geometry with Raster
Photon Hits in R1 when Raster size has radius of 0.2 cm
Moller rate -vs- length of a single taerget
0.5 cm radius -vs- Z
Target is a one 0.5 cm radius cylinder of length Z.
By how much does the moller rate change at full field ?