LB Thesis NewSNR Corrections

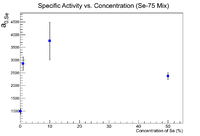
First plot the efficiency corrected activity as a function of concentration. These points are not weighted by mass, but they are fully corrected as per the thesis otherwise. These values are the activity at the highest value of N/B

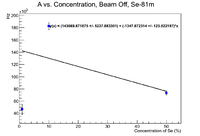
This plot doesn't look very good as the 50% sample has a lower activity than the 10% sample. Try plotting this at the time of beam off. Note these are done using fits with the accepted half life vs. the experimental half life. The error bars represent |(Free Fit A) - (Fixed Fit A)|

Perhaps the difference comes from the fact that the irradiation times were different, but to normalize to a standard beam time, a reference material must be used. Segebade says "Since, as already mentioned, yield values are normalized for a common exposure period of one hour, the following expression is required, which converts the individual activities yielded using other irradiation times to those after standard exposure period T (1h):

[math] N(T) = \frac{A_{0,el}}{A_{0,Ni}} \times \frac{(1-e^{-\lambda_{el}T})}{(1-e^{- \lambda_{el} T_i})} \times \frac{(1-e^{- \lambda_{Ni} T_i})}{(1-e^{-\lambda_{Ni} T})} [/math]

Where [math] T_i [/math] is the actual exposure period and T is the normalized exposure period of 1 hour"

So lets try to correct these ratios using Nickel

For correcting the 50%, we have (note these are the fixed fit values)

[math] N(T) = 0.62 \times \frac{0.52}{0.32} \times \frac{0.01}{0.02} = 0.50 [/math]

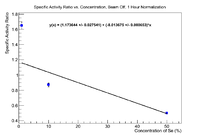
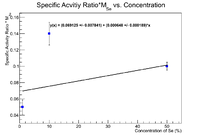
This ratio is lower than its original value (0.62), which makes sense because the nickel would not die off as much in the beam. The 10% and 1% values should not need this correction as they were irradiated for an hour, so the correction goes to unity. Plot the ratio of the specific activity as a function of concentration.

If I apply Dr. Forest's suggested decay correction as were applied to the ratios before (multiply by [math] 1-e^{-\lambda_{el} t_i} [/math], I get

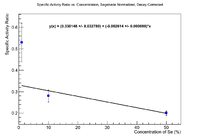
This still doesn't make physical sense. Try multiplying by the mass of the sample to see a change.

This would be the plot Dr. Dale wanted if I used Nickel foils for normalization. It doesn't seem to be physical. As far as I can tell, since we are back to using ratios of activities, the same problems will be encountered that the past year were dedicated to trying to fix, but never were. The largest contributor being a non constant flux across the face of the sample. Perhaps if there were something internal to the soil (Mn-54 search failed), the normalization would be better. Unfortunately I have a feeling the same problems will be encountered (at least in the 0.1% sample because the soil completely filled the Al cylinder, while the Se Pellets had a very small comparative volume.

Se-75 has a different problem, most notably the 50% and 10% samples were reirradiated using different (in mass and volume) Nickel foils. I feel the only solution is to find something internal to the soil to correct to.

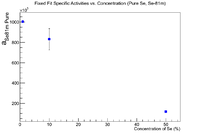
Forced Activities

Each of the following plots are weighted by the mass of the soil.

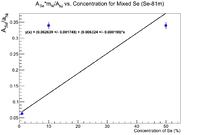
The weighted average of the front inner nickel foil activities is 291179.836 [math] \pm [/math] 2833.73, and the weighted average of the mixed Se pellets is 191004.961 [math] \pm [/math] 4934.62. By forcing all measurements to be these values, the ratio of the specific activity of Ni to Se becomes

[math] \frac{a_{0,Se}}{a_{0,Ni}} = 0.66 \pm 0.018 [/math]

Now multiply by the mass of Se to yield the following plot

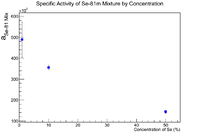
Now plot the Specific Activity vs. Concentration for Se-75's mixed and Pure Se pellets