2NCorr SPDP Introduction
The calculation of angular correlation
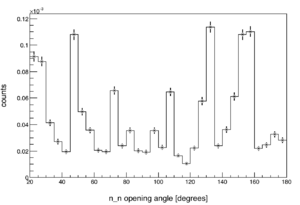
The efficiency and acceptance of the neutron detector array varies chaotically over the range of two-neutron opening angles, denoted by (see figure to the right). This is in part due to the detector array's non-spherically symmetric geometry, and also to its varying efficiency as a function of both particle position and energy.
For this reason, every measured distribution must be made meaningful by normalizing against a measured "control" distribution. The normalization is done by diving the values of a given distribution by the control distribution on a bin-by-bin basis.
.
two-neutron opening angle
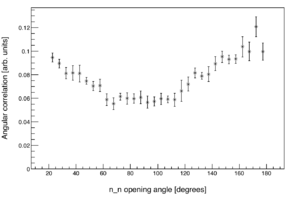
For , the control distribution is made by looking at neutron events from pairs of separate pulses, such that the two pulses occurred within no more than a few 100 ms of each other. If, in a given pair, there is a neutron event in both pulses, then the opening angle between the two events is calculated. Since no information can be shared between the neutrons of different pulses, this distribution must be free of any two-neutron correlations. However, this distribution is subject to the exact same effects of detector geometry and efficiency, as is the distribution formed from pairs of correlated neutrons in single pulses. So here, the words "angular correlation" refer to the measured rate relative to a completely uncorrelated neutron source. The plot (right) is the same data from the plot above after normalization to the uncorrelated distribution.
.
single-neutron absolute theta
Another measurement possible with this set up, is the distribution of the angle between neutron singles, and the direction of the incident photon beam (). When constructing a distribution from neutron singles, the method of using uncorrelated neutron pairs from different pulses no longer works, because while the neutrons in a pair are uncorrelated with each other, they are both correlated with the direction of the incident photon beam. For this reason, neutron singles from the spontaneous fission (SF) of Cf252 are used for normalization. This choice leads to several issues, because there are differences in experimental conditions between the measurement of photo-neutrons in the presence of a photon beam, versus the measurement of neutrons from the SF of Cf252. The energy spectrum of neutrons from Cf252 differ from that of our photo-neutrons. During the Cf252 measurement, the detectors experience much dead-time caused by the detection of photons. Also, the noise profiles are very different. Each of these effects must be removed or neglected by employing various corrections and assumptions, which results in a analysis procedure that is less robust than the same-pulse different-pulse method.
Accidentals and trues
An accidental neutron coincidence, or accidental for short, is defined here as any pair of neutrons that are uncorrelated despite having been produced during the same pulse. One example is a neutron from a (gamma,n) reaction paired with a neutron from a (gamma, fiss) reaction. For another example, consider a pulse that caused two photofission events, such that one fission releases four correlated neutrons and the other releases two, creating 4*2=8 possible distinct pairs of uncorrelated neutrons, or in other words, eight accidentals.
A true neutron coincidence, or true for short, is defined here as any pair correlated neutrons from the same pulse. For example, there are (4*3)/2=6 trues created by a single photofission event that releases 4 correlated neutrons.
During the experiment, measured trues/accidentals always occurred as two-neutron coincidences, as there were never three or more neutrons detected in coincidence.