Known Moller differential cross section

Comparing experimental vs. theoretical for Møller differential cross section 11GeV

Using the equation from [1]

[math]\frac{d\sigma}{d\Omega}=\frac{ e^4 }{8E^2}\left \{\frac{1+cos^4\frac{\theta}{2}}{sin^4\frac{\theta}{2}}+\frac{1+sin^4\frac{\theta}{2}}{cos^4\frac{\theta}{2}}+\frac{2}{sin^2\frac{\theta}{2}cos^2\frac{\theta}{2}} \right \}[/math]

where [math]\alpha=\frac{e^2}{\hbar c}\quad with\quad \hbar = c =1[/math]

This can be simplified to the form

[math]\frac{d\sigma}{d\Omega}=\frac{ \alpha^2 }{4E^2}\frac{ (3+cos^2\theta)^2}{sin^4\theta}[/math]

Plugging in the values expected for a scattering electron:

[math]\alpha ^2=5.3279\times 10^{-5}[/math]

[math]E\approx 53 MeV[/math]

Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around

[math]\frac{5.3279\times 10^{-5}}{4\times 2.81\times 10^{15}eV^2}=4.74\times 10^{-21} eV^{-2}=\frac{4.74\times 10^{-21}}{1eV^2}\times \frac{1\times 10^{18}eV^2 }{1\ GeV^2}=\frac{.0047}{GeV^2}[/math]

The trigonometric function part of the equation comes out to it's minimum of 9 at 90 degrees.

[math]\frac{(3+Cos^2(90))^2}{Sin^4(90)}=9[/math]

Using the conversion of

[math]\frac{1}{1GeV^2}=.3894 mb[/math]

[math]\frac{1\ GeV^{-2}}{.3894\ mb}=\frac{.0047\ GeV^{-2}}{x\ mb}[/math]

We find that the differential cross section scale is [math]\frac{d\sigma}{d\Omega}\approx 1.8\times 10^{-3}mb=1.8\mu b\times 9=17\mu b[/math]

Converting the number of electrons to barns,

[math]L=\frac{i_{scattered}}{\sigma} \approx i_{scattered}\times \rho_{target}\times l_{target}[/math]

where ρ_target is the density of the target material, l_target is the length of the target, and i_scattered is the number of incident particles scattered.

For a ammonia target,

Ammonia density:

[math]\rho = \frac{.8 g}{cm^3}[/math]

Molecular weight calculation:

[math]\frac{14.0067 g}{1 mole} + \frac{1.00794 g}{1 mole}\times 3=\frac{17 g}{1 mole}[/math]

[math]\rho_{target}\times l_{target}=\frac{.8 g}{1 cm^3}\times \frac{1 mole}{17 g} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^2}{barn} =2.82\times 10^{-2} barns[/math]

For 400 million incoming electrons

[math]\frac{1}{\rho_{target}\times l_{target} \times 4 \times 10^9}=8.87\times 10^{-9} barns[/math]

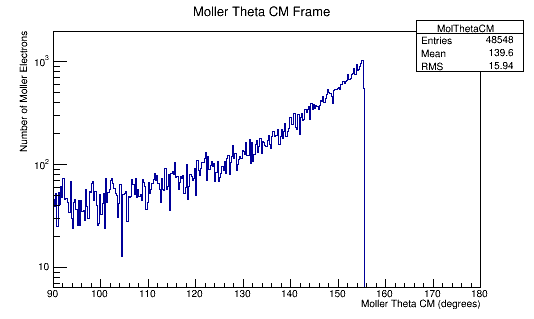
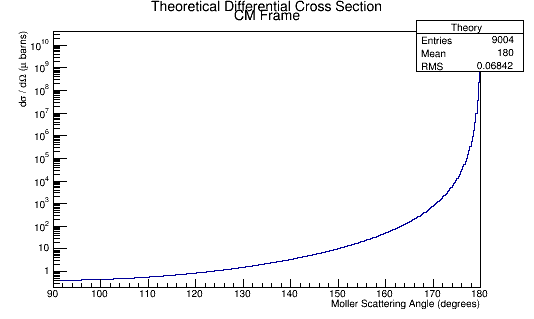
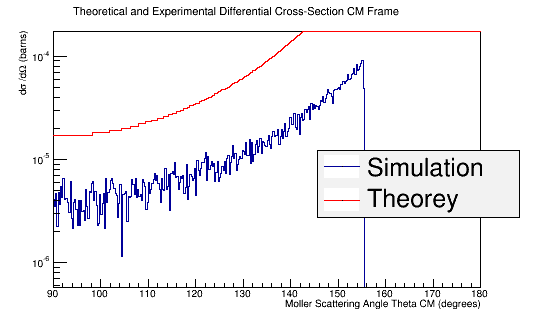
Combining these plots, and rescaling the Final Theta in the Center of Mass for micro-barns:

Scaling factor:

[math]\frac{8.87\times 10^{-8} barns}{17\mu b}=5.2\times 10^{-3}[/math]

TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
Combo->Add(MolThetaCM,5.2e-3);
Combo->Draw();
Theory->Draw("same");