Two Dimensional Oscillators
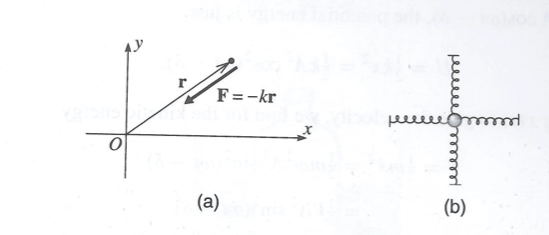
- [math] \vec F = -k_x x \hat i + k_y y \hat j)[/math]
- Potential
- [math]U = - \int \vec F \cdot d \vec r = k_x \int x dx + k_y \int y dy = \frac{1}{2} \left ( k_x x^2 + k_y y^2 \right )[/math]
Isotropic Oscillator
The simplest 2-D oscillator that is composed of identical springs (same spring constant).
- [math] \vec F = -k( x \hat i + y \hat j)[/math]
The equations of motion are separable two equations, one for each direction
- [math]\ddot x = - \omega^2x \Rightarrow x = A_x \cos(\omega t - \delta_x)[/math]
- [math]\ddot y = - \omega^2 y \Rightarrow y = A_y \cos(\omega t - \delta_y)[/math]
you could define a relative phase between the two oscillators as
- [math]\delta = \delta_y - \delta_x[/math]
it can be substituted into the above equations by shifting the time origin (problem 5.15)
let
- [math]t^{\prime} = t + t_0[/math]
then
- [math]x = A_x \cos(\omega t^{\prime} - \omega t_0 - \delta_x)[/math]
let
- [math]t_0 = \frac{-\delta_x}{\omega}[/math]
- [math] x=A_x \cos(\omega t^{\prime} - \omega\frac{-\delta_x}{\omega} - \delta_x)[/math]
- [math] =A_x \cos(\omega t^{\prime})[/math]
similarly
- [math]y = A_y \cos(\omega t^{\prime} - \omega t_0 - \delta_x)[/math]
- [math] =A_y \cos(\omega t^{\prime} - \omega \frac{-\delta_x}{\omega} - \delta_x)[/math]
- [math]= A_y \cos(\omega t^{\prime} +\delta_x - \delta_y)[/math]
- [math]= A_y \cos(\omega t^{\prime} -\delta)[/math]
Interpretation
- [math] =A_x \cos(\omega t^{\prime})[/math]
- [math]= A_y \cos(\omega t^{\prime} -\delta)[/math]
There are several modes of motion for the above system of equation
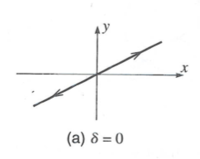
No phase difference
If there is no phase difference then (\delta =0 ) and you have oscillating motion along a line.
90 degree phase difference
If the x and y motions are completely out of phase ( phase difference of 90 degrees or [math]\frac{\pi}{2}[/math])
then the motion is an ellipse (unless their amplitudes are equal in which case the mass moves in a circle).

- [math] =A_x \cos(\omega t^{\prime})[/math]
- [math]= A_y \cos(\omega t^{\prime} +\frac{\pi}{2})= A_y \sin(\omega t^{\prime})[/math]
- [math] \left (\frac{x}{A_x} \right )^2 + \left (\frac{y}{A_y} \right )^2 = \cos^2(\omega t^{\prime}) + \sin^2(\omega t^{\prime})= 1[/math]
The above is an equation of a circle if [math]A_x=A_y[/math] otherwise it is an ellipse with semi-major and semi-minor axes [math]A_x[/math] and [math]A_y[/math]
If the phase shift is less than 90 then the ellipse is slanted towards the x-axis otherwise it is toward the y-axis.
Anisotropic Oscillator
Consider the case of having two different spring constants in each direction
- [math] \vec F = -k_x x \hat i - k_y y \hat j[/math]
The equations of motion are separable two equations, one for each direction
- [math]\ddot x = - \omega^2_x x \Rightarrow x = A_x \cos(\omega_x t - \delta_x)= A_x \cos(\omega_x t^{\prime})[/math]
- [math]\ddot y = - \omega^2_y y \Rightarrow y = A_y \cos(\omega_y t - \delta_y)= A_y \cos(\omega_y t^{\prime} - \delta)[/math]
where
- [math]\delta = \delta_y - \delta_x[/math]
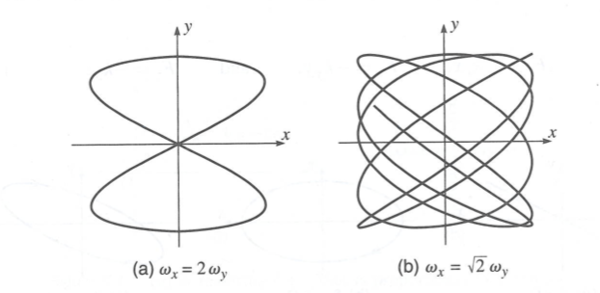
Lissajous figure
if
- [math]\frac{\omega_x}{\omega_y} =[/math] rational number (a fraction formed two integers, denominator is non-zero)
Forest_UCM_Osc#2-D_Oscillators



