The C.M. frame is often chosen to theoretically calculate cross-sections even though experiments are conducted in the Lab frame. In such cases you will need to transform cross-sections between two frames.
The total cross-section should be frame independent
- [math]\sigma_{C.M.} = \sigma_{Lab}[/math]
or
- [math]\sigma(\theta) d \Omega = \sigma(\psi) d \Omega^{\prime}[/math]
where
[math]\theta[/math] is in the CM frame and [math]\psi[/math] is in the Lab frame.
- A non-relativistic transformation
- [math]\sigma(\theta) d \Omega = \sigma(\psi) d \Omega^{\prime}[/math]
- [math]\sigma(\theta) 2 \pi \sin(\theta) d \theta = \sigma(\psi) 2 \pi \sin (\psi) d \psi[/math]
- [math]\Rightarrow \sigma(\psi) = \frac{\sin(\theta)}{\sin(\psi)} \frac{d \theta}{d \psi} \sigma(\theta)[/math]
The transformation is governed by the dependence of [math]\theta[/math] on [math] \psi[/math] [math] \left( \frac{d \theta}{d \psi} \right )[/math]
Lets return back to our picture of the scattering Process
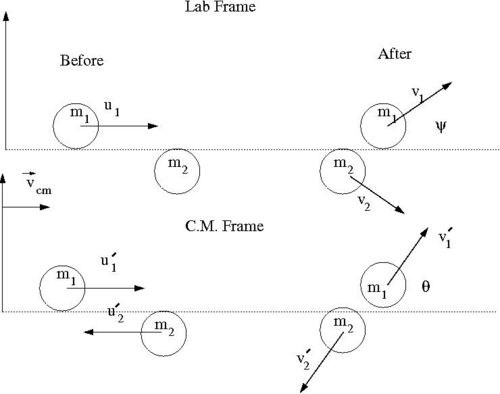
if we superimpose the vectors [math]\vec{v}_1[/math] and [math]\vec{v}_1^{\prime}[/math] we have
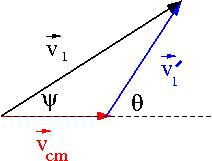
Trig identities (non-relativistic Gallilean transformation) tell us
[math]v_1 \sin(\psi) = v_1^{\prime} \sin(\theta)[/math]
[math]v_1 cos(\psi) = v_{cm} + v_1^{\prime} \cos(\theta)[/math]
solving for [math]\psi[/math]
[math]\tan(\psi) = \frac{\sin(\psi)}{\cos(\psi)} = \frac{v_1^{\prime} \sin(\theta)/v_1}{\frac{v_{CM}}{v_1} + \frac{v_1^{\prime} \cos(\theta)}{v_1} }
= \frac{\sin(\theta)}{\cos(\theta) + \frac{v_{CM}}{v_1^{\prime}}}[/math]
For an elastic collision only the directions change in the CM Frame: [math]u_1^{\prime}= v_1^{\prime}[/math] & [math]u_1^{\prime}= v_2^{\prime}[/math]
- From the definition of the C.M.
- [math]\vec{v}_{CM} = \frac{m_1 \vec{u}_1 + m_2 \vec{u}_2}{m_1+m_2} = \frac{m_1}{m_1+m_2} \vec{u}_1[/math]
- conservation of momentum in CM Frame [math]\Rightarrow[/math]
- [math]m_1 u_1^{\prime} = - m_2 u_2{\prime}[/math]
- [math] \Rightarrow v_1^{\prime} = u_1^{\prime} = \frac{-m_2}{m_1} u_2^{\prime}[/math]
- Gallilean Coordinate transformation
- [math]\vec{u}_1 = \vec{u}_1^{\prime} + \vec{v}_{CM} = \vec{u}_1^{\prime} + \frac{m_1}{m_1+m_2} \vec{u}_1[/math]
- [math]\Rightarrow u_1{\prime} = \left [ 1 - \frac{m_1}{m_1 + m_2} \right ] u_1 = \frac{m_2}{m_1+m_2}u_1[/math]
- [math]\Rightarrow v_1^{\prime} = u_1^{\prime} =\frac{m_2}{m_1+m_2} u_1[/math]
- another expression for [math]\psi[/math]
using the above gallilean transformation we can do the following
- [math]\frac{v_{CM}}{v_1^{\prime}}= \frac{\frac{m_1}{m_1+m_2} u_1}{\frac{m_2}{m_1+m_2} u_1} = \frac{m_1}{m_2}[/math]
or
- [math]\tan(\psi) = \frac{\sin(\theta)}{\cos(\theta) + \frac{m_1}{m_2}}[/math]
after a little trig substitution
[math]\Rightarrow \frac{m_1}{m_2} = \frac{sin(\theta - \psi)}{\sin(\psi)} =[/math] constant
now use the chain rule to find [math]\frac{d \theta}{d \psi}[/math]
- [math]f \equiv \frac{sin(\theta - \psi)}{\sin(\psi)} =[/math] constant
- [math]df = 0 = \frac{ \partial f}{\partial \psi} d \psi + \frac{ \partial f}{\partial \theta} d \theta [/math]
- [math]\Rightarrow \frac{d \theta}{d \psi} = \frac{-\frac{ \partial f}{\partial \psi} }{\frac{ \partial f}{\partial \theta} }[/math]
- [math]-\frac{ \partial f}{\partial \psi} = \frac{\cos(\theta - \psi)}{\sin(\psi)} + \frac{\sin(\theta - \psi)}{\sin(\psi)}[/math]
- [math]\frac{ \partial f}{\partial \theta }= 1 + \frac{\sin(\theta - \psi) \cos(\psi)}{\cos(\theta - \psi) \sin(\psi)}[/math]
after substitution:
- [math]\sigma(\psi) = \frac{\sin(\theta)}{\sin(\psi)} \frac{d \theta}{d \psi} \sigma(\theta)[/math]
- [math]=\frac{\sin(\theta)}{\sin(\psi)} \left [ 1 + \frac{\sin(\theta - \psi) \cos(\psi)}{\cos(\theta - \psi) \sin(\psi)} \right ] \sigma(\theta)[/math]
For the above equation to be more useful one would prefer to recast it in terms of only [math]\psi[/math] and masses.
- [math]\sigma(\psi) = \frac{\left [ \frac{m_1}{m_2}\cos(\psi) + \sqrt{1-\left ( \frac{m_1 \sin(\psi) }{m_2} \right )^2 }\right ]}{\sqrt{1 - \left ( \frac{m_1 \sin(\psi)}{m_2}\right )^2 }}\sigma(\theta)[/math]
Forest_UCM_NLM#Galilean_Transformations

