Sadiq Thesis Latex
overlay positron energy distribution at T1 with what is seen at T2 for several values of Q7 Put the e+ simulated results results with experimentally detected results. Flux weighted cross section for positron production. Put the scintilator calibration in the thesis: Mean of ADC9 vs charge on the scope. Separate simulated and experimental systematic errors, then put them together in conclusions.
Text
Anstract
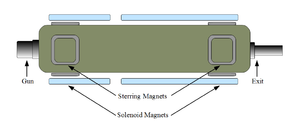
\chapter{Apparatus} \section{HRRL Beamline} A 16~MeV S-band (2856~MHz RF frequency) High Repetition Rate Linac (HRRL) located in the Department of Physics Beam Lab at Idaho State University is used to impinge a 12~MeV electron beam onto a tungsten foil. The energy of the HRRL is tunable between 3 to 16~MeV and its repetition rate variable from 1 to 300~Hz. The operating range of the HRRL is given in Table~\ref{tab:hrrl-par}. As shown in Figure~\ref{fig:app-hrrl-cavity}, the HRRL has a thermionic gun, vertical and horizontal steering magnet sets on two ends, and two solenoid magnets.
Introduction
\chapter{Introduction}
\section{Positron Beam}
Positrons are used in several disciplines of science, such as chemistry, physics, material science, surface science, biology and nanoscience~\cite{Chemerisov:2009zz}. Different approaches are used to generate positrons. The main challenge is increasing the intensity (or current) of the positron source. One of the most common methods used to generate a positron beam is using an electron linear accelerator (linac). The electron beam produces positrons by bremsstrahlung and pair production. One of the advantages of the linac based positron beam is its variable energy and intensity. Below are two examples that use positrons as probes.
\subsection{Positron Beam for Positron Annihilation Spectroscopy} Positron Annihilation Spectroscopy (PAS) is a non-damaging technique to detect defects in materials. PAS has become a useful method to investigate the microstructure of condensed matter and to detect small sized defects at low concentration at different depths which are hardly detectable with other traditional techniques~\cite{Prochazka2001}. Different depths of the materials can be probed by using a variable energy positron source such as one driven by a linac.
When positrons intercept materials, they lose energy in a process of thermalization that lowers the kinetic energy of positrons below 0.1~eV. %lose energy via ionisation, electron-hole excitations, and the scattering off phonons. Thermalized positrons move towards the defects within materials due to Coulomb repulsion by positive ion cores~\cite{Prochazka2001} where they eventually annihilate. Positrons have a longer life time in defects because of the lower electron density in the defects. Thus defect rich materials exhibit longer positron life times. One may measure concentration and types of defects in the analyte.
\subsection{Positron Beam for Measuring The Impact of Two Photon Exchange} %Low energy positron beam Nucleon electromagnetic form factors are fundamental quantities that are related to the charge and magnetization distribution in the nucleon. Conventionally, the nucleon form factors are measured using the Rosenbluth Technique (RT)~\cite{Rosenbluth1950}. The form factor scaling ratio, \begin{math}R=\mu _p G_{Ep} / G_{Mp}\end{math}, measured using this technique is around unity as shown (hollow squares) in Figure~\ref{rosen-com-RPT}~\cite{PhysRevD.49.5671}. Since the 1990's, a technique using elastic electron-proton polarization transfer to measure this ratio has been developed~\cite{PhysRevD.49.5671, PhysRevC.68.034325, WalkerThesis1989}. In this technique, R has been observed to decrease when the momentum transfer (\begin{math}Q^2\end{math}) increases, as shown (solid circles) in Figure~\ref{rosen-com-RPT}.
\begin{figure}[htbp] \centering \includegraphics[scale=0.70]{1-Introduction/Figures/Sadiq_thesis_mot_RT_RPT_2.png} \caption{Form factor ratio (R), obtained using the Rosenbluth Technique (hollow squares)~\cite{Rosenbluth1950} and from the Recoil Polarization Technique (solid circles)~\cite{PhysRevC.68.034325}.} \label{rosen-com-RPT} \end{figure}
The disagreement could arise from the Rosenbluth Technique's assumption that only one photon is exchanged (OPE) during the scattering while two photon exchange (TPE), which depends weakly on \begin{math}Q^2\end{math}, could become considerable with increasing \begin{math}Q^2\end{math}~\cite{PhysRevC.68.034325}. The contribution of TPE can be obtained by comparing the ratio of \begin{math}e^+~p\end{math} to \begin{math}e^-~p\end{math} scattering. The interference of OPE and TPE can also be studied in the scattering process \begin{math}e^+e^- \rightarrow p\bar p\end{math}~\cite{Arrington2004}.
\section{Positron Beam Generation from Bremsstrahlung}
When a moving charged particle interacts with the electric field of another charged particle, it can be deflected and lose energy in the form of photons, as shown in Figure~\ref{fig:Theo-Brem}. This interaction is known as the bremsstrahlung process. The probability of this interaction increases with the square of the atomic number of the material traversed by the incident charged particle. Figure~\ref{fig:Brems_photon_Ene} shows the photon energy distribution produced when the 12~MeV electron energy distribution from Figure~\ref{fig:Theo-Brems_ele_Ene} interacts with a 1~mm thick tungsten target. As shown in Figure~\ref{fig:Brems_photon_Ene}, the distribution peaks at 0.3~MeV.
\begin{figure}[htbp] \centering \includegraphics[scale=0.40]{1-Introduction/Figures/bremsstrahlung/brems2.eps} \caption{Photon emission from the bremsstrahlung processes.} \label{fig:Theo-Brem} \end{figure}
The bremsstrahlung cross section given is by~\cite{brms-cors} \begin{equation} d \sigma = 4 Z^2r_e^2 \alpha \frac{d \nu}{\nu} \left \{ \left (1 + \left( \frac{E}{E_0} \right )^2 \right ) \left [ \frac{\phi_1(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] - \frac{2E}{3E_0} \left [ \frac{\phi_2(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] \right \}, \label{eq:Brem-cross} \end{equation} \noindent where $E_0$ is initial total energy of the electron, $E$ is the final total energy of the electron, $\nu = \frac{E_0-E}{h}$ is frequency of the emitted photon, and $Z$ is atomic number of the target. $\gamma = \frac{100 m_ec^2 h \nu}{E_0 E Z^{1/3}}$ is the charge screening parameter, and $f(Z)$ is given by \begin{equation} f(Z) = (Z \alpha)^2 \sum_1^{\infty} \frac{1}{ n [ n^2 + (Z \alpha)^2]}, \end{equation} \noindent where $\alpha = \frac{1}{137}$ is the fine-structure constant, $\phi_1$ and $\phi_2$ are screening functions that depend on Z. \begin{figure}[htbp] \centering \includegraphics[scale=0.70]{1-Introduction/Figures/En_photon_dnT1_logY_2.eps} \caption{Bremsstrahlung photon energy distribution produced when the 12~MeV electron energy distribution from Figure~\ref{fig:Theo-Brems_ele_Ene} interacts with the simulation's 1~mm thick tungsten target.} \label{fig:Brems_photon_Ene} \end{figure} \begin{figure}[htbp] \centering \includegraphics[scale=0.70]{1-Introduction/Figures/En_e_upT1.eps} \caption{The electron energy distribution incident on a tungsten foil in simulation.} \label{fig:Theo-Brems_ele_Ene} \end{figure}
There are three competing processes that a photon can undergo when interacting with matter. Figure~\ref{fig:Theo-3pro-in-W} illustrates the cross-sections for different interactions that can occur when a photon traverses tungsten as a function of photon energy. At electron volt (eV) energies, which are comparable to the electron atomic binding energy, the dominant photon interaction is the photoelectric effect. As the photon energy increases up to the kilo electron volt (keV) range, the Compton scattering process starts to be more dominant. Although the photon is totally absorbed during the photoelectric effect, photons merely lose energy when undergoing Compton scattering. As the photon energy reaches twice the rest mass energy of the electron, $i.e.$ 2 \begin{math} \times \end{math} 511~keV, pair production begins to occur. Pair production becomes the dominant interaction process when photon energies are beyond 5~MeV~\cite{Krane}. In this process, a photon interacts with the electric field of the nucleus or the bound electrons and is converted into an electron and positron pair.
\begin{figure}[htbp] \centering \includegraphics[scale=0.44]{1-Introduction/Figures/xcom/10.eps} \caption{The cross-sections for different types of photon interactions with tungsten as a function of photon energy~\cite{nistxcom}.} \label{fig:Theo-3pro-in-W} \end{figure}
Using natural units, where \begin{math}c \equiv 1\end{math}, the differential cross-section for pair production can be expressed as \begin{equation} \begin{array}{l} \frac{d \sigma}{d \epsilon_1 d \theta_1 d \theta_2} = 8 \left ( \frac{\pi a}{\sinh (\pi a)} \right )^2 \frac{a^2}{2 \pi} \frac{e^2}{\hbar c} \left ( \frac{\hbar}{m_e c }\right )^2 \frac{\epsilon_1 \epsilon_2}{k^3} \theta_1 \theta_2 \\ \\ \times \left \{ \frac{V^2(x)}{q^4} \left [ k^2 (u^2 + v^2) \xi \eta - 2 \epsilon_1 \epsilon_2 (u^2 \xi^2 + v^2 \eta^2 ) + 2 (\epsilon_1^2 + \epsilon_2^2)uv \xi \eta cos(\phi) \right ] \right . \\ \\ \left . + a^2W^2(x) \xi^2 \eta^2 \left [ k^2(1 - (u^2+v^2)\xi \eta - 2 \epsilon_1 \epsilon_2 (u^2 \xi^2 + v^2 \eta^2) -2 (\epsilon_1^2 + \epsilon_2^2) u v \xi \eta \cos(\phi)\right ]\right \}, \\ \end{array} \end{equation}
\noindent where $k$ is photon energy, $\theta_{1}$ and $\theta_2$ are the scattering angle of $e^+$ and $e^-$ respectively, $ \phi = \phi_1 - \phi_2$ is the angle between the $e^+$ and $e^-$ pair, $\epsilon_1$ and $\epsilon_2$ are the energy of the positron and electron respectively. Other constants are $u = \epsilon_1 \theta_1$, $v=\epsilon_2 \theta_2$, $\xi = \frac{1}{1+u^2}$, $\eta= \frac{1}{1+v^2}$, $q^2 = u^2 + v^2 + 2 u v \cos(\phi)$, $x= 1-q^2 \xi \eta$, $a = \frac{Ze^2}{\hbar c}$, $V(x) = 1 + \frac{a^2}{(1!)^2} + \frac{a^2 (1+a^2) x^2}{(2!)^2} + \frac{a^2 (1+a^2)(2^2+a^2)x^4 x^2}{(3!)^2} + \cdots$, and $W(x) = \frac{1}{a^2} \frac{d V(x)}{d x}$.
In pair production, positron and electron pairs are created back to back in the center of mass frame. In the lab frame, electrons and positrons tend to move in the direction of the photon, as shown in Figure~\ref{fig:Theo-pair-pro}. The positron and electron carry away the energy from the photon that is in excess of 1.022~MeV. In the center of mass frame, the kinetic energy is equally shared. Photons with an energy above 1.022~MeV in the bremsstrahlung spectrum of Figure~\ref{fig:Brems_photon_Ene} have the potential to create electron and positron pairs. Figure~\ref{fig:Theo-brem} is the simulation of 10 million 12~MeV mono energetic electrons impinging on a 1.016~mm thick tungsten target. Turning on the annihilation process resulted in a 511~keV peak on top of the bremsstrahlung spectrum. This 511~keV peak represents photons produced when the created positrons from the pair production annihilate with atomic electrons inside the tungsten target.
\begin{figure}[htbp] \centering \includegraphics[scale=0.40]{1-Introduction/Figures/Pair_Production/Pair_Production.eps} \caption{Pair production.} \label{fig:Theo-pair-pro} \end{figure} \begin{figure}[htbp] \centering \includegraphics[scale=0.50]{1-Introduction/Figures/pair/on/Eng2.eps} \\ \caption{Photon spectrum of created by million 12~MeV mono energy electrons impinging on a 1.016~mm thick tungsten target.} \label{fig:Theo-brem} \end{figure}
\section{Emittance Measurement} When the emittance and Twiss parameters are given at the exit of a linac, one will be able to calculate the beam size and the divergence at any given point along the beamline. To optimized positron production, one needs to know the beam size and divergence on the production target. Emittance and Twiss parameters are the input parameters for any accelerator simulation tools used to study beam transport and make predictions of the beam properties along the beam line.
\subsection{Emittance} In accelerator physics, a Cartesian coordinate system is used to describe the motion of the accelerated particles. As shown in Figure~\ref{fig:coordinates}, the $s$-axis of the Cartesian coordinate system is defined as the natural coordinate that is oriented along the same direction as the beam momentum. The $x$-axis and $y$-axis are horizontal and vertical coordinates which constitute the transverse beam profile. The transverse beam profiles are described as a function of the longitudinal coordinates, $x(s)$ and $y(s)$.
\begin{figure}[htbp] \centering \includegraphics[scale=0.7]{1-Introduction/Figures/coordinates.eps} \caption{Coordinated system and reference orbit (dashed line)~\cite{Conte}.} \label{fig:coordinates} \end{figure}
The phase space $x'$ vs. $x$ of the beam is an ellipse with invariant area (along the beamline). Here $x'$ is defined as \begin{equation} x'=\frac{dx}{ds}. \label{eq:divergence} \end{equation} \noindent This invariant is called the Courant-Snyder invariant~\cite{Conte}. The transverse emittance $\epsilon$ of the beam is defined to be the area of the ellipse that contains 90\% of the particles. Beam divergence and Twiss parameters are related to the beam size and divergence by \begin{equation} \sigma_{x}(s)=\sqrt{\epsilon _x (s) \beta _x (s)},~ \sigma_{x'}(s)=\sqrt{\epsilon _x (s) \gamma _x (s)}, \label{eq:twiss-emit} \end{equation} \noindent where $\epsilon_{x}$ is beam's horizontal emittance, $\sigma_{x}$ is the beam size's rms, $\sigma_{x'}$ is the beam divergence's rms, and $\beta _x $ and $\gamma _x$ are two of the three Twiss parameters.
\subsection{Emittance Measurement} The HRRL beam emittance was measured using optical transition radiation (OTR). This transition radiation was theoretically predicted by Ginzburg and Frank~\cite{Ginzburg-Frank} in 1946 to occur when a charged particle passes the boundary of two media. An OTR based viewer was installed to observe the electron beam size at 37.2~mA electron peak currents, available using the HRRL at 15~MeV with 200~ns macro pulse width. The visible light is produced when a relativistic electron beam crosses the boundary of two media with different dielectric constants.
Light is emitted in a conical shape at backward angles with the peak intensity at an apex angle of $\theta = 1/\gamma$ with respect to the incident electron's angle of reflection. A 15 MeV electron accelerated by the HRRL would emit light at $\theta = 2^\circ$. Orienting the OTR target at 45${^\circ}$ with respect to the incident electron beam will result in the high intensity photons being observed at an angle of 90${^\circ}$ with respect to the incident beam, see Figure~\ref{q-scan-layout}. These backward-emitted photons are observed using a digital camera and can be used to measure the shape and the intensity of the electron beam based on the OTR distribution. Although an emittance measurement can be performed in several ways~\cite{emit-ways, sole-scan-Kim}, the quadrupole scanning method~\cite{quad-scan} was used to measure the emittance and Twiss parameters in this work.
\subsection{Quadrupole Scanning Method} Fig.~\ref{q-scan-layout} illustrates the beamline components used to measure the emittance for the quadrupole scanning method. A quadrupole is positioned at the exit of the linac to focus or de-focus the beam as observed on the OTR view screen. The 3.1~m distance between the quadrupole and the screen was chosen in order to minimize chromatic effects and to satisfy the thin lens approximation. %The quadrupole and the screen are located far away to minimize chromatic effects and to increase the veracity of the thin lens approximation used to calculate beam optics. \begin{figure}[htbp] \centering \includegraphics[scale=0.55]{1-Introduction/Figures/quad_scan_setup2.eps} \caption{Apparatus used to measure the beam emittance.} \label{q-scan-layout} \end{figure} Assuming the thin lens approximation, $\sqrt{k_1}L << 1$, is satisfied, the transfer matrix of a quadrupole magnet may be expressed as % thin lens approximation (sqrt{k1}*L << 1). In our case sqrt{k1}*L =0.07 \begin{equation} \label{quad-trans-matrix} \mathrm{\mathbf{Q}}=\Bigl(\begin{array}{cc} 1 & 0\\ -k_{1}L & 1 \end{array}\Bigr)=\Bigl(\begin{array}{cc} 1 & 0\\ -\frac{1}{f} & 1 \end{array}\Bigr), \end{equation} where $k_{1}$ is the quadrupole strength, $L$ is the length of quadrupole, and $f$ is the focal length. A matrix representing the drift space between the quadrupole and screen is given by \begin{equation} \label{drift-trans-matrix} \mathbf{\mathbf{S}}=\Bigl(\begin{array}{cc} 1 & l\\ 0 & 1 \end{array}\Bigr), \end{equation} where $l$ is the distance between the scanning quadrupole and the screen. The transfer matrix $\mathbf{M}$ of the scanning region is given by the matrix product $\mathbf{SQ}$. In the horizontal plane, the beam matrix at the screen ($\mathbf{\sigma_{s}}$) is related to the beam matrix of the quadrupole ($\mathbf{\sigma_{q}}$) using the similarity transformation \begin{equation} \mathbf{\mathbf{\sigma_{s}=M\mathrm{\mathbf{\mathbf{\sigma_{q}}}}}M}^{\mathrm{T}}. \end{equation} where the $\mathbf{\sigma_{s}}$ and $\mathbf{\sigma_{q}}$ are defined as~\cite{SYLee} \begin{equation} \mathbf{\mathbf{\sigma_{s,\mathnormal{x}}=}}\Bigl(\begin{array}{cc} \sigma_{\textnormal{s},x}^{2} & \sigma_{\textnormal{s},xx'} \\ \sigma_{\textnormal{s},xx'} & \sigma_{\textnormal{s},x'}^{2} \end{array}\Bigr) ,\; \mathbf{\mathbf{\sigma_{q,\mathnormal{x}}}}=\Bigl(\begin{array}{cc} \sigma_{\textnormal{q},x}^{2} & \sigma_{\textnormal{q},xx'}\\ \sigma_{\textnormal{q},xx'} & \sigma_{\textnormal{q},x'}^{2} \end{array}\Bigr). \end{equation} \noindent %By defining the new parameters~\cite{quad-scan}, $A \equiv \sigma_{11},~B \equiv \frac{\sigma_{12}}{\sigma_{11}},~C \equiv\frac{\epsilon_{x}^{2}}{\sigma_{11}}$ By defining the new parameters~\cite{quad-scan} \begin{equation} A \equiv l^2\sigma_{\textnormal{q},x}^{2},~B \equiv \frac{1}{l} + \frac{\sigma_{\textnormal{q},xx'}}{\sigma_{\textnormal{q},x}^{2}},~\text{and}~C \equiv l^2\frac{\epsilon_{x}^{2}}{\sigma_{\textnormal{q},x}^{2}}, \end{equation} the matrix element $\sigma_{\textnormal{s},x}^{2}$, the square of the beam size's rms at the screen, may be expressed as a parabolic function of the product of $k_1$ and $L$ \begin{equation} \sigma_{\textnormal{s},x}^{2}=A(k_{1}L)^{2}-2AB(k_{1}L)+(C+AB^{2}). \label{par_fit} \end{equation}
The emittance measurement was performed by changing the quadrupole current, which changes $k_{1}L$, and measuring the corresponding beam image size on the view screen. The measured two-dimensional beam image was projected along the image's abscissa and ordinate axes. A Gaussian fitting function is used on each projection to determine the rms value, $\sigma_{\textnormal{s}}$ in Eq.~(\ref{par_fit}). Measurements of $\sigma_{\textnormal{s}}$ for several quadrupole currents ($k_{1}L$) are then fit using the parabolic function in Eq.~(\ref{par_fit}) to determine the constants $A$, $B$, and $C$. The emittance ($\epsilon$) and the Twiss parameters ($\alpha$ and $\beta$) can be found using Eq.~(\ref{emit-relation}) \begin{equation} \epsilon=\frac{\sqrt{AC}}{l^2},~\beta=\sqrt{\frac{A}{C}},~\alpha=\sqrt{\frac{A}{C}}(B+\frac{1}{l}). \label{emit-relation} \end{equation}
Apparatus
\chapter{Apparatus} \section{HRRL Beamline} A 16~MeV S-band (2856~MHz RF frequency) High Repetition Rate Linac (HRRL) located in the Department of Physics Beam Lab at Idaho State University is used to impinge a 12~MeV electron beam onto a tungsten foil. The energy of the HRRL is tunable between 3 to 16~MeV and its repetition rate variable from 1 to 300~Hz. The operating range of the HRRL is given in Table~\ref{tab:hrrl-par}. As shown in Figure~\ref{fig:app-hrrl-cavity}, the HRRL has a thermionic gun, vertical and horizontal steering magnet sets on two ends, and two solenoid magnets.
\begin{table} \centering \caption{The Basic Parameters of the HRRL.} \begin{tabular}{lcc} \toprule {Parameter} & {Unit} & {Value} \\ \midrule maximum energy & MeV & 16 \\ peak current & mA & 100 \\ repetition rate & Hz & 300 \\ absolute energy spread & MeV & 2-4 \\ macro pulse length & ns & $>$50 \\ \bottomrule \end{tabular} \label{tab:hrrl-par} \end{table}
\begin{figure}[htbp] \centering %\includegraphics[scale=0.6]{3-Apparatus/Figures/HRRL_Cavity.eps} \includegraphics[scale=0.6]{2-Apparatus/Figures/HRRL_Cavity4.png} \caption{The configuration of the HRRL cavity.} \label{fig:app-hrrl-cavity} \end{figure}
The accelerator's cavity was relocated to the position shown in Figure~\ref{fig:app-hrrl-line} to provide enough space for a beam line that can transport either positrons or electrons. The beam elements are described in Table~\ref{tab:app-hrrl-coordinates}. Quadrupole and dipole magnets were added to the new beam line as well as diagnostic tools like an OTR and YAG screens. Faraday cups and toroids were installed to measure the electron beam size and the current. Energy slits were installed to control the energy/momentum spread of the beam after the first dipole. A 1.016~mm thick retractable tungsten foil target (T1) was placed between the 1st and 2nd quadrupole triplets and used to produce positrons when the electron beam interacts with it. The room where the HRRL is located is divided by a wall into two parts; the accelerator side and the experimental cell. A beam pipe at the end of the 90 degree beamline goes through a hole in the wall and delivers the beam from the accelerator side to the experimental cell. The positron detection system consisting of two NaI detectors was placed at the end of the beamline in the experimental cell side as shown in Figure~\ref{fig:app-hrrl-line}.
\begin{sidewaysfigure} \centering \includegraphics[scale=0.3]{2-Apparatus/Figures/HRRL_line2.eps} \caption{The HRRL beamline layout and parts.} \label{fig:app-hrrl-line} \end{sidewaysfigure}
\begin{table} \centering \caption{The HRRL Beamline Parts and Coordinates.} \begin{tabular}{lll} \toprule {Label} & {Beamline Element} & {Distance from} \\ {} & {} & {Linac Exit (mm)} \\ \midrule Q1 & quadrupole & 335 \\ Q2 & quadrupole & 575 \\ Q3 & quadrupole & 813 \\ T1 & e$^+$ production target & 1204 \\ Q4 & quadrupole & 1763 \\ Q5 & quadrupole & 2013 \\ Q6 & quadrupole & 2250 \\ D1 & dipole & 2680 \\ S1 & OTR screen & 3570 \\ FC1 & Faraday cup & 3740 \\ EnS & energy slit & 3050 \\ S2 & YAG screen & 3410 \\ Q7 & quadrupole & 3275 \\ D2 & dipole & 3842 \\ FC2 & Faraday cup & 4142 \\ Q8 & quadrupole & 4044 \\ Q9 & quadrupole & 4281 \\ Q10 & quadrupole & 4571 \\ T2 & annihilation target & 7381 \\ \bottomrule \end{tabular} \label{tab:app-hrrl-coordinates} \end{table}
\section{The OTR Imaging System} The OTR target is a 10~$\mu$m thick aluminum foil with a 1.25 inch diameter. The OTR is emitted in a cone shape with the maximum intensity at an angle of $1/\gamma$ with respect to the reflecting angle of the electron beam~\cite{OTR-Gitter}. Three two inch diameter lenses are used for the imaging system to avoid optical distortion at lower electron energies. The focal lengths and positions of the lenses are shown in Figure~\ref{image_sys}. The camera used is a JAI CV-A10GE digital camera with a 767 by 576 pixel area. The images were taken by triggering the camera synchronously with the electron gun. \begin{figure}[htbp] \centering {\scalebox{0.35} [0.35]{\includegraphics{2-Apparatus/image_sys2.eps}}} {\scalebox{0.40} [0.40]{\includegraphics{2-Apparatus/MOPPR087f3}}} \caption{The OTR imaging system.} \label{image_sys} \end{figure}
\section{Positron Detection} When the electron beam is incident on T1, photons and secondary electrons are created along with positrons. These particles are the main source of noise in the experiment. The positrons were transported to the second tungsten target (T2) which was shielded from this noise by the concrete wall and Pb bricks. The setup is shown in Figure~\ref{fig:HRRL-pos-det-setup}. A 6-way cross was placed at the end of the beamline to hold T2. The 6-way cross has three 1~mil (0.0254 millimeters) thick stainless steel windows. The two horizontal windows perpendicular to the beamline allowed the 511~keV photons created from the positron annihilation to escape the beamline with limited attenuation. A third window at the end of the 90 degree beamline was used as the beam exit. Two NaI detectors were placed facing the two exit windows to detect the photons produced in T2. A two inch thick lead brick collimator with a 2 inch diameter hole was placed between the exit window and NaI detector. A scintillator (Scint) and a Faraday cup (FC3) were placed at the end of the beamline and were used to tune the electron and positron beam. When positrons reach T2, they can thermalize and annihilate inside T2. During thermalization, a positron loses its kinetic energy. When it annihilates with an electron, two 511~keV photons are emitted back to back. A triplet coincidence is required between the accelerator RF pulse and the detection of a photon in each NaI detector.
\begin{figure}[htbp] \centering \includegraphics[scale=0.50]{2-Apparatus/HRRL_Pos_detection2.eps} \caption{The positron detection system: T2 (pink) was placed with 45$^\circ$ angle to the horizontal plane first, then rotated 45$^\circ$ along the vertical axis.} \label{fig:HRRL-pos-det-setup} \end{figure}
\subsection{NaI Detectors}
NaI crystals, shown in Figure~\ref{fig:PMT}, were used to detect 511~keV photons from positron annihilation. Originally, the detectors had pulse signal lengths around 400~$\mu$s. New PMT bases were built to use the HV divider shown in Figure~\ref{fig:PMT_base}. A picture of the constructed bases is shown in Figure~\ref{fig:new_base_made}. The pulse length of the new PMT bases is about 1~$\mu$s. The NaI crystal is from Saint-Gobain Crystal \& Detectors (Mod. 3M3/3) with a dimension of $3 \times 3$. The operating high voltage of -1150~V would position the 511~keV photons within the range of the charge sensing ADC (CAEN Mod. V792).
\begin{table} \centering \caption{The Radioactive Sources and Corresponding Photon Peaks.} \begin{tabular}{lccc} \toprule {Radioactive Sources} & Unit & First Peak & Second Peak \\ \midrule Co-60 & keV & 1173 & 1332 \\ Na-22 & keV & 511 & 1275 \\ \bottomrule \end{tabular} \label{tab:Na22_Co60} \end{table}
\begin{figure}[htbp]
\centering
\includegraphics[scale=0.4]{2-Apparatus/SAINT-GOBAIN_3M33.png}
\caption{The NaI crystal dimension.}
\label{fig:PMT}
\end{figure}
\begin{figure}[htbp] \centering \includegraphics[scale=0.75]{2-Apparatus/Modified_PMT.png} \caption{The modified PMT base design.} \label{fig:PMT_base} \end{figure}
\begin{figure}[htbp] \centering \includegraphics[scale=0.13]{2-Apparatus/IAC_NaI.png} \caption{The NaI crystals and new bases.} \label{fig:new_base_made} \end{figure}
The NaI detectors were calibrated using a Na-22 and a Co-60 source with the photon peaks indicated in Table~\ref{tab:Na22_Co60}. Figure~\ref{fig:NaI_Co60_Scope} is the oscilloscope image of several Co-60 photon pulses observed by the detector with the new PMT. The calibrated NaI detector spectrum from the Na-22 and Co-60 sources is shown in Figure~\ref{fig:NaI-Calb}. The rms values of the fits on the four peaks shown in Figure~\ref{fig:NaI-Calb} are $\sigma_{Na, 511}=18.28\pm0.04$~keV, $\sigma_{Na, 1275}=44.51\pm0.27$~keV, $\sigma_{Co, 1173}=42.49\pm0.24$~keV, and $\sigma_{Co, 1332}=50.30\pm0.39$~keV.
\begin{figure}[htbp] \centering \includegraphics[scale=0.4]{2-Apparatus/NaI_Co60_Scope.png} \caption{Detector output pulses using the Co-60 source and new PMT. The amplitude of the pulse is about 60~mV. The rise time of the pulse is larger than 50 ns, and the fall time is larger than 700~ns.} \label{fig:NaI_Co60_Scope} \end{figure}
\begin{figure}[htbp] \centering \includegraphics[scale=0.8]{2-Apparatus/Figures/NaI_Calbration/NaI_Calb7.eps} \caption{The calibrated NaI spectrum of Na-22 and Co-60 sources.} \label{fig:NaI-Calb} \end{figure}
The Na-22 source was placed between two NaI detectors to measure the spectrum when the RF was on, represented by dotted line (no electrons were fired from accelerator gun), and off, represented by dashed line in Fig~\ref{fig:NaI-peak-shift}. The solid line in Fig~\ref{fig:NaI-peak-shift} represents the photon spectrum created by 3~MeV positrons impinging on T2. The 511 keV peak in the right NaI detector was shifted to the right side of the spectrum by 17 channels when the RF was on as shown in Figure~\ref{fig:NaI-peak-shift} (a) while in the left NaI detector the peak shifted to the left by 28 channels as shown if Figure~\ref{fig:NaI-peak-shift} (b). When the RF was on, no difference was observed for photon peaks created by Na-22 source and 3~MeV positrons. The photon peak created by Na-22 source shifted when the RF was off.
\begin{figure}[htbp] \begin{tabular}{ccc} \centerline{\scalebox{0.6} [0.6]{\includegraphics{2-Apparatus/Figures/RunDec2012/PeakShiftNaIL8.eps}}}\\ (a) Left NaI detector. \\ \\ \\ \centerline{\scalebox{0.6} [0.6]{\includegraphics{2-Apparatus/Figures/RunDec2012/PeakShiftNaIR8.eps}}} \\ (b) Right NaI detector.\\ \end{tabular} \caption{The 511~keV peak observed using NaI detectors shifted when accelerator RF was on. The spectrum were taken with RF on (dotted line) and with RF off (dashed line). The solid line represents the photon spectrum created by 3~MeV positrons impinging on T2.} \label{fig:NaI-peak-shift} \end{figure}
\subsection{The DAQ Setup}
The data acquisition (DAQ) setup and timing diagram is shown in Figure~\ref{fig:daq-setup}. The last dynode signals from left and right NaI detectors were inverted using a ORTEC 474 inverting amplifier and sent to an CAEN Mod. N842 constant fraction discriminator (CFD). An electron gun pulse generated VETO sent to CFD prevented the RF noise from triggering the CFD. The CFD generated multiple digital pulses for a single signal received. A GG 8000-01 octal gate generator was used to create a single 1~$\mu$s wide pulse from the first pulse in order to ignore the multiple CFD pulses produced by a single analog output pulse from the detector. The coincidence was formed between the gun pulse and the 1~$\mu$s wide pulse from each detector using a LeCroy model 622 logic module as given by \begin{equation} \text{NaI~Left~\&\&~NaI~Right~\&\&~Gun~Trigger}. \end{equation}
The ADC requires 5.7~$\mu$s to convert the analog signal to a digital signal. The logic module output was delayed 6~$\mu$s by a dual timer (CAEN Mod. N93B) to accommodate the ADC's conversion time and trigger the DAQ. The ADC (CAEN Mod. V792) converted the NaI detector's analog signals to digital when a 1~$\mu$s gate created by gun pulse using a dual timer was present as shown in the lower part of Figure~\ref{fig:daq-setup}. The ADC was fast cleared unless a veto signal created using a dual timer was received from the inverted output of logic module.
\begin{sidewaysfigure}[htbp] \centering \includegraphics[scale=0.68]{2-Apparatus/Figures/DAQ_Logic_all.eps} \caption{The DAQ setup and timing diagram.} \label{fig:daq-setup} \end{sidewaysfigure}
%When there is a trigger in the ADC, the data in the ADC is read
Simulation
\chapter{Simulation} Simulations were performed using G4beamline~\cite{muonsinc} to study the processes of position generation and transportation. ``G4beamline is a particle tracking and simulation program based on the GEANT4~\cite{geant4} toolkit that is specifically designed to easily simulate beamlines and other systems using single-particle tracking~\cite{muonsinc}. The simulation predicts that at least one positron is created per 1000 incident 10~MeV electrons. A large amount of beam loss was observed during the initial simulation. As a result, the simulation was divided into three steps based on the locations along the beamline that saw more than 90\% beam loss. A new beam event generator was created based on the results of the previous step in the simulation.
The first step generated an electron beam with the energy distribution that was observed in the experiment shown in Figure~\ref{fig:En-Scan}. The electrons were focused by three quadrupoles onto the target T1, see Figure~\ref{fig:app-hrrl-line}. Electrons transversing T1 produced bremsstrahlung photons of sufficient energy to produce $e^+e^-$ pairs. The second step simulated the transportation of positrons exiting T1 to the entrance of the first dipole D1. The third step transported positrons from the entrance of D1 to the annihilation target T2, the interactions of positrons with T2, and the detection of the resulting 511~keV photon pairs.
\section{Step 1 - The Electron Beam Generation and Transportation to T1} In the first simulation step, an electron beam was generated with an energy distribution that was observed in the experiment. The emittance, the Twiss parameters, and the energy distribution of the electron beam were measured experimentally and used to generate the electron beam. The energy distribution of the electron beam is shown in Figure~\ref{fig:En-Scan}. The distribution was fit using two skewed Gaussian distributions. The fit parameters given in Table~\ref{tab:En-Scan_resluts} were used to generated electrons.
A series of virtual detectors were placed along the beamline to sample the beam. As an example, three virtual circular detectors and T1 are shown in Figure~\ref{fig:T1_UpD_DwD2}. The electron beam was detected by a virtual detector DUPT1 (Detector UPstream of T1) placed 25.52~mm upstream of T1. Positrons, electrons, and photons generated during the interaction of the electron beam with T1 were observed by virtual detectors DT1 (Detector of T1) and DDNT1 (Detector DowNstream of T1) placed 25.52~mm downstream of T1. %In Figure~\ref{fig:SimS1_pos_En_DDNT1}, $13.8 \times 10^{10}$ electrons shot at T1 and generated positrons positrons shown in blue.
\begin{figure}[htbp] \centering \includegraphics[scale=0.50]{3-Simulation/Figures/sim_setup_T1_UpD_DwD2.png} \caption{T1 is the positron production target. DUPT1 is a virtual detector located upstream of T1 to detect the incoming electron beam. DDNT1 is a virtual detector downstream of T1. DT1 is a virtual detector that is placed right after T1 parallel to it.} \label{fig:T1_UpD_DwD2} \end{figure}
\subsection{The Positron Beam on DDNT1}
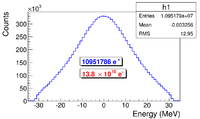
In the first step, $1.38 \times 10^{10}$ electrons were generated with the energy distribution shown by the dotted dashed line in Figure~\ref{fig:SimS1_T1UPDN}, transported to T1, and created the positrons represented by solid the line. The dashed line is the electron energy distribution observed by DDNT1. Instead, the simulation result of $1.38 \times 10^{7}$ electrons incident on T1 is drawn in Figure~\ref{fig:SimS1_T1UPDN}. The incident electrons were detected by the virtual detector DUPT1 and downstream positrons and electrons were detected by DDNT1.
\begin{figure}[htbp] \centering \includegraphics[scale=0.80]{3-Simulation/Figures/s/s1/overlay6.eps} \caption{Energy distribution of incident electrons (dotted dashed line), electrons after T1 (dashed line) and created positrons (solid line). The incident electron distribution counts were weighted by 0.001.} \label{fig:SimS1_T1UPDN} \end{figure}
\begin{figure}[htbp] \begin{tabular}{cc} {\scalebox{0.4} [0.4]{\includegraphics{3-Simulation/Figures/X_e+_DDNT1.eps}}} & {\scalebox{0.4} [0.4]{\includegraphics{3-Simulation/Figures/Y_e+_DDNT1.eps}}} \\ (a) $x$ projection. & (b) $y$ projection. \\ {\scalebox{0.4} [0.4]{\includegraphics{3-Simulation/Figures/XP_e+_DDNT1.eps}}} & {\scalebox{0.4} [0.4]{\includegraphics{3-Simulation/Figures/YP_e+_DDNT1.eps}}} \\ (c) $x$ projection of the divergence. & (d) $y$ projection of the divergence.\\ {\scalebox{0.42} [0.4]{\includegraphics{3-Simulation/Figures/XY_e+_DDNT1.png}}} & {\scalebox{0.42} [0.4]{\includegraphics{3-Simulation/Figures/XY_e+_DDNT1_zoom.png}}} \\ (e) The transverse beam profile. & (f) The transverse beam profile zoomed in. \\ \end{tabular} \caption{The transverse beam projections and angular distributions of positrons detected.} \label{fig:DDNT1_results} \end{figure}
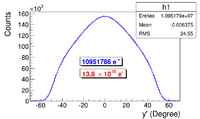
The positron spatial distribution detected by DDNT1 is shown in Figure~\ref{fig:DDNT1_results}. The $y$ $vs.$ $x$ spatial distribution of the beam is shown in Figure~\ref{fig:DDNT1_results}~(e) and Figure~\ref{fig:DDNT1_results} (f). As can be seen from Figure~\ref{fig:DDNT1_results} (b) and (d), the $y$ spatial distribution and divergence, defined in equation~\ref{eq:divergence}, of the positron beam have a sharp drop in counts in the region between $-25.8$~mm and $-27.2$~mm from the beam center. Figure~\ref{fig:sim-DDNT1-T1-geo} shows the geometry and location of T1 and DDNT1. If the size of T1 were to be increased, it would eventually intersect with DDNT1 at a distance between $25.8$~mm and $27.2$~mm from the beam center, $i.e.$ the edge of the T1 is facing this $1.4$~mm wide low count area. %This is the result of the target's thickness of 1.016 mm and the 45$^{\circ}$ angle of intersection ($1.016\sqrt{2}=1.44$). The edge of the target does not produce many positrons compared to the face of the target. \begin{figure}[htbp] \centering \includegraphics[scale=0.9]{3-Simulation/Figures/sharp_drop2.eps} \caption{The geometry of the target T1 and the virtual detector DDNT1.} \label{fig:sim-DDNT1-T1-geo} \end{figure}
As shown in Figure~\ref{fig:DDNT1_YpY}, the $y$ distribution count decreases at $\theta$ = 45$^{\circ}$. Positrons were emitted from both the downstream and upstream side of T1. Positrons from the downstream side of T1 intersected the detector at angles below 45$^{\circ}$ while positrons from the upstream side of T1 begin to hit the detector at angles beyond 45$^{\circ}$. Neither positrons upstream nor downstream of T1 traveled to the 1.4~mm wide low count area. Only positrons created on the edge of T1 reached the low count area between 25.8~mm~$<x<$~27.2~mm. As a result, the counts in this area are comparatively lower.
\begin{figure}[htbp] \begin{tabular}{cc} {\scalebox{0.4} [0.4]{\includegraphics{3-Simulation/Figures/STSimS1_YYP_DDNT1.png}}} & {\scalebox{0.4} [0.4]{\includegraphics{3-Simulation/Figures/STSimS1_YYP_DDNT1_zoom.png}}} \\ (a) y' $vs.$ y. & (b) y' $vs.$ y zoom. \\ \end{tabular} \caption{The positron beam $y'$ $vs$. $y$ detected by DDNT1.} \label{fig:DDNT1_YpY} \end{figure}
\subsection{The Positron Beam on Virtual Detectors DQ4 and DD1}
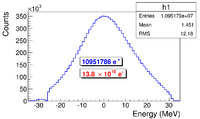
The positron beam energy distribution on virtual detectors DQ4 (Detector placed at the entrance of Q4) and DD1UP (Detector placed at the UPstream entrance of D1) are shown in Figure~\ref{STSimS1_En_DQ4_DD1}. Nearly 90\% of the positrons are lost when transported from DQ4 to DD1UP due to the large positron divergence. %484.4 mm from T1 to DQ4. 1476.4 mm from T1 to DD1UP. 992 mm from DQ4 to DD1UP.
\begin{figure}[htbp] \begin{tabular}{ccc} \centerline{\scalebox{0.6} [0.6]{\includegraphics{3-Simulation/Figures/En_e+_DQ4.eps}}} \\ (a) The positron energy distribution on DQ4. \\ \centerline{\scalebox{0.6} [0.6]{\includegraphics{3-Simulation/Figures/En_e+_DD1.eps}}}\\ (b) The positron energy distribution on DD1. \\ \end{tabular} \caption{The positron beam energy distribution detected downstream of T1.} \label{STSimS1_En_DQ4_DD1} \end{figure}
\section{Step 2 - The Transportation of The Positron Beam from DDNT1 to The Entrance of The First Dipole}
The beam observed on detector DDNT1 in step 1 was used to generate positrons for the second step. At detector DDNT1, the higher energy positrons tend to have smaller polar angles and are closer to the beam center. Positrons were generated in 1~keV/c momentum bins with different weights, spatial, and angular distributions. The positrons are generated at DDNT1 (where they were sampled) and transported to the entrance of D1 through a quadrupole triplet as shown in Figure~\ref{fig:STSimSetupS2}. The virtual detectors were placed at the entrance of Q4 (DQ4) and D1 (DD1UP) to track the positrons. The beam observed at DD1UP would be used to generate positrons in the third step.
\begin{figure}[htbp] \centering \includegraphics[scale=0.60]{3-Simulation/Figures/STSimSetupS2_3.png} \caption{The generation and transportation of the positron beam in step 2. The virtual detectors were used to track the positrons.} \label{fig:STSimSetupS2} \end{figure}
\section{Step 3 - The Transportation of Positrons from the Entrance of The First Dipole to T2 and The Detection of 511~keV Photons}
In this step, the positron beam was generated at the entrance of the first dipole (DD1UP). The beam was bent $90^{\circ}$ by two dipoles and transported to the annihilation target T2 located at the end of the beamline as shown in Figure~\ref{fig:T2}.
\begin{figure}[htbp] \centering \includegraphics[scale=0.4]{3-Simulation/Figures/HRRL_T2_2.png} \caption{T2 and virtual detectors located upstream (DT2UP) and downstream (DT2DN) of T2 are shown at the center of the figure. NaI detectors and Pb shielding are located horizontally at two sides.} \label{fig:T2} \end{figure}
As shown in Figure~\ref{fig:T2}, two virtual circular detectors DT2UP and DT2DN with a 48~mm diameter (48~mm is the inner diameter of the beam pipe) were placed upstream and downstream of T2 to detect positrons. Two other detectors, DT2L and DT2R with the same diameters as T2 were placed on the beam left and right side parallel to T2 to detect positrons. Two virtual detectors were placed horizontally at the locations of NaI detectors, which were 170~mm away from the beamline center, to detect photons. Two inch thick Pb bricks with 2-inch diameter circular openings were positioned between T2 and the virtual detectors. Each detector was surrounded by 2$$ of Pb. When a positron annihilates inside T2, two back-to-back scattered 511~keV photons are generated. An event is registered in the simulation when both NaI detectors observe a 511~keV photon.
\subsection{Positrons Detected by The Detection System}
The detector efficiency chart shown in Figure~\ref{fig:NaI_Ef}, obtained from Saint-Gobain Crystals~\cite{NaI-Eff}, indicates the NaI crystal has an efficiency of 68\% for 511~keV photons. If two detectors are operated in coincidence mode, the detection efficiency of the system is $68\% \times 68\%~=~46.24\%$. Figure~\ref{fig:e+_Generated_and_Detected} shows the number of 511~keV photon pairs detected in coincidence mode (multiplied by 46.24\%) and overlaid with the positrons that are detected on DDNT1.
\begin{figure}[htbp] \centering \includegraphics[scale=0.60]{3-Simulation/Figures/NaI_Ef_3.png} \caption{NaI detector efficiency obtained from Saint-Gobain Crystals~\cite{NaI-Eff}. The lines correspond to the different crystal sizes (in inches)shown on the right side of the figure.} \label{fig:NaI_Ef} \end{figure}
\begin{figure}[htbp] \centering \includegraphics[scale=0.70]{3-Simulation/Figures/overlay/e+_Generated_and_Detected.eps} \caption{Positrons detected on virtual detector DDNT1 and 511~keV photon pairs detected by the NaI detectors in coincidence mode when Q7 is at 0~A, 3.5~A and 10~A.} \label{fig:e+_Generated_and_Detected} \end{figure}
\subsection{Beam Loss Study} The positron distribution observed after T1 was used to send a sample of positrons towards the dipole D1 that would be used to create a positron event generator at the entrance to dipole D1. This procedure was repeated at D1 in order to generate a large positron sample at the annihilation target (T2). This three step procedure reduced the simulation time to generate large positron samples. $7.253 \times 10^{16}$ electrons incident on the T1 created $5.756 \times 10^{13}$ positrons as shown in Column 2 of Table~\ref{tab:sim-S2E}. Columns 2 and 3 in Table~\ref{tab:sim-S2E} represent the number of positrons that would need to be generated in order to observe the number of positrons in the remaining columns. The number of 511~keV photon pairs detected by NaI detectors in coincidence mode are shown in the last column of Table~\ref{tab:sim-S2E}. The number of positrons observed by virtual detectors placed along the beamline and 511~keV photon pairs detected are shown in Figure~\ref{fig:TransEff}.
\begin{sidewaystable} \centering \caption{Predicted Number of Positrons Transported and The Number of 511~keV Photons Detected.} \begin{tabular}{lccccccccc} %\begin{tabular}{lllllllllll} \toprule Energy & On & Enter & Enter & Exit & Enter & Enter & Exit & Reach & $\gamma$ on \\ (MeV) & DDNT1 & Q4 & D1 & D1 & Q7 & D2 & D2 & T2 & NaI \\ \midrule $1.02 \pm 0.25$ & $2.5 \times 10^{12} $ & $1.4 \times 10^{10} $ & $1.4 \times 10^{9} $ & $1.2 \times 10^{8}$ & $2.6 \times 10^{7} $ & $2.7 \times 10^{6} $ & $1.2 \times 10^{6} $ & $4.3 \times 10^{3} $ & $7$\\ $1.50 \pm 0.25$ & $4.9 \times 10^{12} $ & $2.7 \times 10^{10} $ & $2.8 \times 10^{9} $ & $1.8 \times 10^{8}$ & $9.1 \times 10^{7} $ & $2.7 \times 10^{7} $ & $1.2 \times 10^{7} $ & $5.1 \times 10^{4} $ & $97 $\\ $2.15 \pm 0.25$ & $6.5 \times 10^{12} $ & $3.8 \times 10^{10} $ & $3.8 \times 10^{9} $ & $3.8 \times 10^{8}$ & $1.7 \times 10^{8} $ & $7.8 \times 10^{7} $ & $3.6 \times 10^{7} $ & $4.4 \times 10^{5} $ & $734 $\\ $2.50 \pm 0.25$ & $6.8 \times 10^{12} $ & $4.1 \times 10^{10} $ & $4.1 \times 10^{9} $ & $4.4 \times 10^{8}$ & $2.3 \times 10^{8} $ & $1.1 \times 10^{8} $ & $5.0 \times 10^{7} $ & $4.6 \times 10^{5} $ & $794 $\\ $3.00 \pm 0.25$ & $6.6 \times 10^{12} $ & $4.1\times 10^{10} $ & $4.1 \times 10^{9} $ & $4.6 \times 10^{8}$ & $2.7 \times 10^{8} $ & $1.3 \times 10^{8} $ & $6.1 \times 10^{7} $ & $4.5 \times 10^{5} $ & $723 $\\ $3.50 \pm 0.25$ & $6.1 \times 10^{12} $ & $3.9 \times 10^{10} $ & $3.9 \times 10^{9} $ & $4.4 \times 10^{8}$ & $2.8 \times 10^{8} $ & $1.4 \times 10^{8} $ & $6.7 \times 10^{7} $ & $4.4 \times 10^{5} $ & $716 $\\ $4.02 \pm 0.25$ & $5.3 \times 10^{12} $ & $3.5 \times 10^{10} $ & $3.5 \times 10^{9} $ & $4.1 \times 10^{8}$ & $2.7 \times 10^{8} $ & $1.4 \times 10^{8} $ & $6.9 \times 10^{7} $ & $4.3 \times 10^{5} $ & $702 $\\ $4.50 \pm 0.25$ & $4.6 \times 10^{12} $ & $3.1 \times 10^{10} $ & $3.1 \times 10^{9} $ & $3.6 \times 10^{8}$ & $2.5 \times 10^{8} $ & $1.3 \times 10^{8} $ & $6.7 \times 10^{7} $ & $4.0 \times 10^{5} $ & $646 $\\ $5.00 \pm 0.25$ & $3.8 \times 10^{12} $ & $2.7 \times 10^{10} $ & $2.7 \times 10^{9} $ & $3.1 \times 10^{8}$ & $2.2 \times 10^{8} $ & $1.2 \times 10^{8} $ & $6.2 \times 10^{7} $ & $3.6 \times 10^{5} $ & $566 $\\ $5.50 \pm 0.25$ & $3.0 \times 10^{12} $ & $2.2 \times 10^{10} $ & $2.2 \times 10^{9} $ & $2.6 \times 10^{8}$ & $1.9 \times 10^{8} $ & $1.0 \times 10^{8} $ & $5.6 \times 10^{7} $ & $3.3 \times 10^{5} $ & $533 $\\ \bottomrule \end{tabular} \label{tab:sim-S2E} \end{sidewaystable}
\begin{figure}[htbp] \centering \includegraphics[scale=0.80]{3-Simulation/Figures/Transporation_Efficiency/Ef.eps} \caption{Predicted number of positrons transported. Black cube: positrons incident on DDNT1. Red cube: positrons entered Q4. Blue cube: positrons entered D1. Magenta cube: positrons exited D1. Black circle: positrons entered Q7. Red circle: positrons entered D2. Blue circle: positrons exited D2. Magenta circle: positrons incident on DT2UP. Black triangle: 511~keV photons detected by NaI detectors in coincidence mode.} \label{fig:TransEff} \end{figure}
As shown in Table~\ref{tab:sim-S2E}, the positron energy distribution is divided into 10 bins. At detector DDNT1 (25.8~mm after T1), there are about $10^{12}$ positrons in each bin. At the entrance of Q4, the number of positrons dropped two orders of magnitude. This may be attributed to the solid angle that the entrance of Q4 makes with respect to T1, if one assumes T1 is a point source of positrons. The distance between T1 and the virtual detector DQ4 is $560$~mm and the radius of DQ4 is $24$~mm. The solid angle of the DQ4 is $\Omega_{\text{Q4}}=\frac{\pi r^2}{d^2}=\frac{\pi 24^2}{560^2}$~rad. Positrons make up a cone with a 45$^\circ$ half angle, which is $\Omega_{\text{beam}}=0.6\pi$~rad in solid angle. The ratio of the two solid angles, $\Omega_{\text{Q4}}/\Omega_{\text{beam}}$, is 1:160, $i.e.$ 1 out of 160 positrons make it from T1 to DQ4, assuming that the positron beam is isotropic inside the cone. However, the positron beam peaks at a smaller angle as shown in Figure~\ref{fig:DDNT1_results} (c) and (d) and as a result more positrons are transported from DDNT1 to DQ4, resulting in a ratio closer to 1:100.
In a simulation where the dipoles were set to transport 3~MeV positrons, the beam energy distribution at the exit of D1, entrance of Q7, exit of Q7, entrance of D2, exit of D2, and T2 are shown in Figure~\ref{fig:dipole-trans} and Table~\ref{tab:pos-beam-loss}. In Table~\ref{tab:pos-beam-loss}, the relative counts reported in the last column are obtained by dividing the second column by 723, the number of 511~keV photons detected by NaI detectors in coincidence mode.
\begin{table} \centering \caption{The Positron Beam Loss along the Beamline When Dipoles Set to Transport 3~MeV Positrons.} \begin{tabular}{lcc} \toprule {Beam Sample} & {Absolute Counts} & {Relative Counts} \\ {Locations} & {} & {} \\ \midrule e$^+$ on DDNT1 & $6.6\times10^{12}$ & $9.4\times10^{10}$ \\ e$^+$ enter Q4 & $4.1\times10^{10}$ & $5.8\times10^{7}$ \\ e$^+$ enter D1 & $4.1\times10^{9}$ & $5.8\times10^{6}$ \\ e$^+$ exit D1 & $4.6\times10^{8}$ & $6.6\times10^{5}$ \\ e$^+$ enter Q7 & $2.7\times10^{8}$ & $3.8\times10^{5}$ \\ e$^+$ enter D2 & $1.3\times10^{8}$ & $1.9\times10^{5}$ \\ e$^+$ exit D2 & $6.1\times10^{7}$ & $8.7\times10^{4}$ \\ e$^+$ on T2 & $4.4\times10^{5}$ & $6.3\times10^{2}$ \\ e$^+$ annihilated in T2 & $2.5\times10^{5}$& $3.6\times10^{2}$ \\ 511~keV photons on NaI & 723 & 1 \\
\bottomrule \end{tabular} \label{tab:pos-beam-loss} \end{table}
The dipoles in the simulation were set to transport 3~MeV positrons to the annihilation target T2, where 58\% of the positrons annihilated and created 511~keV photon pairs. 0.7\% of the photon pairs are lost when passing through the vacuum windows. The left NaI detector observed 2897 511~keV photons and the right one detected 4100. The ratio of 511~keV photon pairs created in T2 to those that made it to the right and the left NaI are 88:1 and 62:1 respectively. This is comparable to the solid angle made by out going photons to the solid angle made by a NaI detector.
The distance between the NaI detectors and the beamline center is 170~cm. The Pb shielding has a hole facing T2 with a 2 inch diameter. Assuming positrons annihilated at the center of T2, the solid angle made by a NaI detector is $\Omega=\frac{\pi r^2}{d^2}=\frac{\pi 25.4^2}{170^2}$~rad. The 511~keV photons created during the annihilation make a solid angle of $2\pi$~rad considering each side of T2 is facing one detector. The ratio of $2\pi$~rad to solid angle of T2 is about 90:1.
1518 511~keV photon pairs are detected by NaI detectors in coincidence mode. The ratio of 511~keV photon pairs created to the ones detected in coincidence mode is 168:1. Counting photons in coincidence mode with the 46.24\% detection efficiency of the system cut the rate in half.
\begin{figure}[htbp] \centering \includegraphics[scale=0.70]{3-Simulation/Figures/Transporation_Efficiency/En2.eps} \caption{Positrons transported when dipoles are set to bend 3~MeV positrons.} \label{fig:dipole-trans} \end{figure}
\subsection{Analysis of the Photon Count Asymmetry in NaI Detectors} In the simulation of section 3.3.2, the right NaI detector observed more 511~keV photons than the left. Eight virtual NaI detectors were placed as shown in Figure~\ref{fig:NaI-detectors} to study this count asymmetry. The orientation of T2 with respect to the incident positron beam was simulated for three cases. In the first case, the photon count rate was predicted by the simulation when the face norm of T2 is parallel to the beam. In the second case, T2 was rotated clockwise (starting with the T2 location in the first case) about the x-axis (axis points beam left) by 45$^\circ$ leaving the upstream side of T2 facing downward as shown in Figure~\ref{fig:NaI-detectors} (a). In the third case, T2 was rotated clockwise about the y-axis (axis points beam up) by 45$^\circ$ such that it is facing the beam right NaI detector as shown in Figure~\ref{fig:NaI-detectors} (b). The setup in the third case is similar to the setup in the experiment and the simulation in section 3.3.2. The 511~keV photon counts observed by eight virtual NaI detectors for one million positrons are given in Table~\ref{tab:photon-counts-asym} for each configuration.
\begin{figure}[htbp] \begin{tabular}{ccc} \centerline{\scalebox{0.5} [0.5]{\includegraphics{3-Simulation/Figures/Photon_Counts_Asymmetry/FaceDown.png}}}\\ (a) \\ \centerline{\scalebox{0.5} [0.5]{\includegraphics{3-Simulation/Figures/Photon_Counts_Asymmetry/T2Exp.png}}} \\ (b)\\ \end{tabular} \caption{NaI detector locations around T2. The positron beam (blue line) is traveling along the z-axis (into the paper). (a) T2 was rotated clockwise about the x-axis by 45$^\circ$ positioning the upstream side of the T2 such that it faces the bottom NaI detector. (b) T2 was positioned as in the experiment. It was first rotated to the position as in (a), then it was rotated clockwise about the y-axis by 45$^\circ$, positioning the upstream side of the T2 such that it faces the beam right NaI detector.} \label{fig:NaI-detectors} \end{figure}
\begin{table} \centering \caption{Number of 511~keV photons observed by the NaI detectors.} \begin{tabular}{lcccccc} \toprule {T2 Placement} & Exp. & Perp. & Face & Face & Face & Face \\ & & to Beam& Down & Down & Down & Down \\ \midrule {Energy} & 3~MeV & 3~MeV & 3~MeV & 1~MeV & 6~MeV & 10~MeV \\ \midrule {NaI Right} & 18085 & 7610 & 7160 & 10315 & 6209 & 4436 \\ {NaI Left} & 12798 & 7651 & 7114 & 10254 & 6111 & 4487 \\ {NaI Top Right} & 7050 & 7580 & 12964 & 12371 & 14698 & 10636 \\ {NaI Bottom Left} & 7084 & 7609 & 18563 & 20238 & 15989 & 10239 \\ {NaI Top} & 12687 & 7599 & 14810 & 14332 & 16131 & 11479 \\ {NaI Bottom} & 18008 & 7609 & 18874 & 20193 & 16950 & 11181 \\ {NaI Top Left} & 14632 & 7656 & 12818 & 12268 & 14812 & 10735 \\ {NaI Bottom Right}& 18764 & 7623 & 18415 & 20197 & 16004 & 10317 \\ \bottomrule \end{tabular} \label{tab:photon-counts-asym} \end{table}
When T2 was placed perpendicular to the incoming positron beam, the 511~keV photons created inside T2 have the same probability to escape from T2 and reach any one of the detectors. As shown in the third column of Table~\ref{tab:photon-counts-asym}, all eight detectors observed a similar number of photons.
In a separate simulation, T2 was positioned as in the first case and impinged by 1, 3, 6, 10~MeV positrons. The average distance traveled by positrons inside T2 before annihilation was $0.0847 \pm 0.0001$, $0.3006 \pm 0.0004$, $0.511 \pm 0.001$, $0.564 \pm 0.008$~mm for the four energies respectively. In another GEANT4 simulation, T2 was positioned according to the second case and two virtual NaI detectors were placed on the top and the bottom of T2. The bottom detector observed more photons than the top when 511~keV photons were generated 0.3006~mm inside T2 isotropically. Photons are more likely to reach the bottom detector because they would travel through a thinner layer of tungsten to reach the bottom detector.
In the second case, shown in Figure~\ref{fig:NaI-detectors} (a), the left and the right NaI detectors had the lowest counts for 3~MeV positrons as shown in the fourth column of Table~\ref{tab:photon-counts-asym}. There is a smaller detection probability for a photon traversing T2 in the radial direction towards the left/right detectors than the top/bottom surfaces of T2 due to the amount of material.
The average distance traveled by 3~MeV positrons inside T2 before annihilation was $0.3006 \pm 0.0004$~mm. In this case, positrons annihilated near the upstream face of T2. For this reason, the bottom, bottom right, and bottom left NaI detectors (facing the upstream side of T2) observed more photons than the top, top right, and top left as shown in the fourth column of Table~\ref{tab:photon-counts-asym}.
The lower the positron beam energy, the smaller the annihilation depth, and the bigger asymmetry in the counts. As shown in the fourth and fifth columns of Table~\ref{tab:photon-counts-asym}, more/less 511~keV photons were observed on the bottom/top detectors with the 1~MeV positron beam than with the 3~MeV. As the positron beam energy increases, as shown in the sixth and seventh columns of Table~\ref{tab:photon-counts-asym}, the top and bottom detectors observed a similar number of photons, because positrons annihilate more uniformly inside T2 and the asymmetry in the counts decreases. With the increasing positron beam energy, fewer positrons were annihilated inside T2 and more penetrated through, as shown in the top two rows of Table~\ref{tab:photon-counts-asym}.
For the third case, shown in Figure~\ref{fig:NaI-detectors} (b), the top right and left bottom detectors observed the lowest counts, because a photon would need to travel in the radial direction to reach these two detectors as shown in the second column of Table~\ref{tab:photon-counts-asym}. The right, bottom and bottom right (facing upstream face of T2) observed more photons than the left, top, top left.
According to the simulation, the asymmetry in the photon counts was due the average positron annihilation depth and the photon attenuation inside T2. Low energy positrons tend to annihilate and produce photon pairs near the incident surface. The created photons are more likely to be detected from the incident surface. In the experiment and the simulation, the right NaI detector was facing the upstream side of T2 and observed more 511~keV photons than the left.
\section{Quadrupole Triplet Collection Efficiency Study}
In this simulation, 5,475,869,400 positrons were generated at DDNT1 and transported to DD1 to study the quadrupole triplet positron collection and transportation efficiency. Six quadrupole current settings of the triplet system were simulated as shown in Table~\ref{tab:triplet-eff}. For different quadrupole current settings, no significant differences were observed in the number of positrons, transverse beam profiles and momentum distributions. The ratio of positrons generated at DDNT1 to the ones that enter D1 is 1525:1.
\begin{sidewaystable} \centering \caption{Quadrupole Triplet System Collection and Transportation Efficiency Data.} \begin{tabular}{cccccccccccccc} \toprule Q4 & Q5 & Q6 & Entries & $x$ & $\sigma_{x} $ & y & $\sigma_{y}$ & $P_{x}$ & $\sigma_{P_{x}}$ & $P_{y}$ & $\sigma_{P_{y}}$ & $P_{z}$ & $\sigma_{P_{z}}$ \\ \midrule A & A & A & & mm & mm & mm & mm & MeV & MeV & MeV & MeV & MeV & MeV \\ \midrule -1 & 2 & -1 & 3587220 & -0.005 & 12 & 0.030 & 12 & $~~3.0 \times 10^{-5}$ & 0.0461 & -0.00216 & 0.04553 & 3.848 & 1.875 \\ -2 & 4 & -2 & 3591423 & -0.012 & 12 & 0.049 & 12 & $~~2.2 \times 10^{-5}$ & 0.0461 & -0.00211 & 0.04554 & 3.848 & 1.875 \\ 1 & -2 & 1 & 3591509 & -0.009 & 12 & 0.040 & 12 & $-1.5 \times 10^{-5}$ & 0.0462 & -0.00216 & 0.04557 & 3.849 & 1.876 \\ 1 & 2 & 1 & 3589854 & -0.005 & 12 & 0.034 & 12 & $-1.8 \times 10^{-5}$ & 0.0462 & -0.00216 & 0.04556 & 3.849 & 1.876 \\ 2 & -4 & 2 & 3592977 & -0.007 & 12 & 0.032 & 12 & $-3.3 \times 10^{-6}$ & 0.0462 & -0.00217 & 0.04549 & 3.849 & 1.876 \\ 2 & 4 & 2 & 3589495 & -0.004 & 12 & 0.033 & 12 & $~~3.0 \times 10^{-6}$ & 0.0462 & -0.00218 & 0.04554 & 3.849 & 1.875 \\ % & & & & & & & & & & & & & \\ \bottomrule \end{tabular} \label{tab:triplet-eff} \end{sidewaystable}
\section{Systematic Errors}
Systematic errors for the positron counts were estimated by carrying out simulations with different magnet settings as shown in Table~\ref{tab:sim-error}. The magnet settings are indicated in the top three rows of Table~\ref{tab:sim-error}. The transported positron energy is given in the first column. The 511~keV photon pairs counted in coincidence mode ($i.e.$ the original count multiplied by 46.42\%) for different magnet settings are given in the corresponding columns below.
The uncertainty of the magnet power supply is 0.1~A. The ``Max/``Min in the table refers to the Maximum/Minimum magnetic field strength when the magnet coil current is at $I_{\text{max}}$/$I_{\text{min}}$, where $I_{\text{max}}$ = $I_{\text{def}} + 0.1$~A and $I_{\text{min}}$ = $I_{\text{def}} - 0.1$~A. ``def refers to the default magnetic field strength of the magnet.
The average counts and fractional errors are shown in the last two columns of Table~\ref{tab:sim-error}. The fractional error in the 511~keV photon pair counts is calculated by dividing the standard deviation of counts by the counts in default magnet setting, $i.e.$ $\frac{\text{standard deviation of counts}}{\text{counts in defalt setting}}$. %The fractional error in the 511~keV photon pair counts is calculated by dividing the standard deviation of counts at different settings by the counts in default magnet setting, $i.e.$ $\frac{\text{standard deviation of counts}}{\text{counts in defalt setting}}$.
\begin{sidewaystable}
\centering
\caption{Systematic Error Study: Counts of 511~keV Photon Pairs for Different Magnet Settings.}
%\begin{tabular}{cccccccccccc}
\begin{tabular}{lllllllllllll}
\toprule
D1 & Max & Min & Max & Min & Max & Max & Min & Min & Def & & \\
Q7 & Def & Def & Def & Def & Max & Min & Min & Def & Def & & \\
D2 & Max & Min & Def & Def & Def & Def & Def & Def & Def & & \\
\midrule
Energy (MeV)& & & & & & & & & & Average & Fractional Error \\
\midrule
0.765~1.265 & 12 & 2 & 3 & 1 & 1 & 3 & 3 & 0 & 6 & 4 & 57.3 \% \\
1.25~-~1.75 & 95 & 75 & 70 & 86 & 85 & 92 & 129 & 86 & 97 & 90 & 17.6 \% \\
1.85~-~2.35 & 674 & 724 & 737 & 769 & 686 & 747 & 803 & 681 & 734 & 728 & 5.8 \% \\
2.25~-~2.75 & 781 & 755 & 753 & 759 & 772 & 963 & 794 & 763 & 794 & 793 & 8.3 \% \\
2.75~-~3.25 & 739 & 737 & 765 & 752 & 738 & 698 & 738 & 757 & 723 & 739 & 2.7 \% \\
3.25~-~3.75 & 713 & 699 & 747 & 712 & 707 & 751 & 718 & 705 & 716 & 719 & 2.5 \% \\
3.77~-~4.27 & 690 & 708 & 715 & 676 & 704 & 658 & 706 & 715 & 701 & 697 & 2.7 \% \\
4.25~-~4.75 & 627 & 666 & 634 & 646 & 635 & 675 & 637 & 653 & 646 & 646 & 2.5 \% \\
4.75~-~5.25 & 558 & 595 & 594 & 603 & 606 & 688 & 582 & 582 & 566 & 597 & 6.7 \% \\
5.25~-~5.75 & 513 & 536 & 535 & 522 & 525 & 535 & 518 & 544 & 533 & 529 & 1.9 \% \\
\bottomrule \end{tabular} \label{tab:sim-error} \end{sidewaystable}
Experiment
\chapter{Data Analysis}
\section{HRRL Emittance Measurement} A quadrupole scanning method was used to measure the accelerator's emittance. The quadrupole current is changed to alter the strength and direction of the quadrupole magnetic field such that a measurable change in the beam shape is seen by the OTR system. Initially, the beam was steered by the quadrupole indicating that the beam was not entering along the quadrupole's central axis. Several magnetic elements upstream of this quadrupole were adjusted to align the incident electron beam with the quadrupole's central axis. First, the beam current observed by a Faraday cup located at the end of beam line was maximized using upstream steering coils within the linac nearest the gun. Second, the first solenoid nearest the linac gun was used to focus the electron beam on the OTR screen. Steering coils were adjusted to maximize the beam current to the Faraday cup and minimize the deflection of the beam by the quadrupole. A second solenoid and the last steering magnet shown in Figure~\ref{fig:app-hrrl-cavity}, both near the exit of the linac, were used in the final step to optimize the beam spot size on the OTR target and maximize the Faraday cup current. A configuration was found that minimized the electron beam deflection when the quadrupole current was altered during the emittance measurements.
The emittance measurement was performed using an electron beam energy of 15~MeV and a 200~ns long macro pulse of 40~mA electron current. The current in the first quadrupole after the exit of the linac was changed from $-$~5~A to $+$~5~A with an increment of 0.2~A. Seven measurements were taken at each current step in order to determine the average beam width and the variance. Background measurements were taken by turning the linac's electron gun off while keep the RF on. OTR images before and after background subtraction are shown in Figure~\ref{bg}. A small dark current is visible in Figure~\ref{bg} (b) that is known to be generated when electrons are pulled off the cavity wall and accelerated.
\begin{figure}[htbp] \begin{tabular}{ccc} \centerline{\scalebox{0.42} [0.42]{\includegraphics{4-Experiment/Figures/MOPPR087f4.eps}}} \\ (a)\\ \centerline{\scalebox{0.42} [0.42]{\includegraphics{4-Experiment/Figures/MOPPR087f5.eps}}}\\ (b)\\ \centerline{\scalebox{0.42} [0.42]{\includegraphics{4-Experiment/Figures/MOPPR087f6.eps}}}\\ (c) \end{tabular} \caption{Digital image from the OTR screen; (a) an image taken with the beam on, (b) a background image taken with the RF on but the electron gun off, (c) The background subtracted beam image ((a)-(b)).} \label{bg} \end{figure}
The electron beam energy was measured using a dipole magnet downstream of the quadrupole used for the emittance measurements. Prior to energizing the dipole, the electron micro-pulse bunch charge passing through the dipole was measured using a Faraday cup located approximately 50~cm downstream of the OTR screen. The dipole current was adjusted until a maximum beam current was observed on another Faraday cup located just after the 45 degree exit port of the dipole. A magnetic field map of the dipole indicates that the electron beam energy was 15~$\pm$~1.6~MeV.
%\subsection{Data Analysis and Results} Images from the JAI camera were calibrated using the OTR target frame. An LED was used to illuminate the OTR aluminum frame that has a known inner diameter of 31.75~mm. Image processing software was used to inscribe a circle on the image to measure the circular OTR inner frame in units of pixels. The scaling factor can be obtained by dividing this length with the number of pixels observed. The result is a horizontal scaling factor of 0.04327~$\pm$~0.00016~mm/pixel and vertical scaling factor of 0.04204~$\pm$~0.00018~mm/pixel. Digital images from the JAI camera were extracted in a matrix format in order to take projections on both axes and perform a Gaussian fit. The observed image profiles were not well described by a single Gaussian distribution.
The profiles may be described using a Lorentzian distribution, however, the rms of the Lorentzian function is not defined. A super Gaussian distribution was used~\cite{sup-Gau}, because it has a sharper distribution than Gaussian and, unlike Lorentzian, the rms values may be directly extracted. The super Gaussian reduced the Chi-square per degree of freedom by a factor of ten compared to a typical Gaussian fit. The beam spot, beam projections, and fits are shown in Figure~\ref{Gau-SupGaus-fits}. In a typical Gaussian distribution, $\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$, the independent variable $x$ is raised to the 2nd power while in the super Gaussian it is raised to a power smaller than 2. For example, the beam projections shown in Figure~\ref{Gau-SupGaus-fits} were fitted with the super Gaussian distributions. The variable $x$ on the exponent was raised to $0.9053$ ($x$-projection) and $1.0427$ ($y$-projection).
\begin{figure}[htbp] \begin{tabular}{cc} {\scalebox{0.42} [0.4]{\includegraphics{4-Experiment/Figures/Gau_SupGau/Gau_ChiSqaure.eps}}} {\scalebox{0.42} [0.4]{\includegraphics{4-Experiment/Figures/Gau_SupGau/SupGau_ChiSqaure.eps}}} \end{tabular} \caption{Gaussian and super Gaussian fits for beam projections. The beam images is background subtracted image and taken when quadrupole magnets are turned off. Left image is Gaussian fit and right image is super Gaussian fit.} \label{Gau-SupGaus-fits} \end{figure}
Figure~\ref{fig:par-fit} shows the square of the rms ($\sigma^2_{\textnormal{s}}$) $vs$ $k_1L$ for $x$ (horizontal) and $y$ (vertical) beam projections along with the parabolic fits using Eq.~\ref{fig:par-fit}. The emittance and Twiss parameters from these fits are summarized in Table~\ref{tab:results}. The MATLAB~\cite{MATLAB} scripts used to calculate emittance and Twiss parameters are given in appendix B. \begin{figure}[htbp] \begin{tabular}{cc} {\scalebox{0.295} [0.295]{\includegraphics{4-Experiment/Figures/par_fit_x.eps}}} {\scalebox{0.295} [0.295]{\includegraphics{4-Experiment/Figures/par_fit_y.eps}}} \end{tabular} \caption{Square of rms values and parabolic fittings.} \label{fig:par-fit} \end{figure}
\begin{table} \centering \caption{Emittance Measurement Results} \begin{tabular}{lcc} \toprule {Parameter} & {Unit} & {Value} \\ \midrule projected emittance $\epsilon_x$ & $\mu$m & $0.37 \pm 0.02$ \\ projected emittance $\epsilon_y$ & $\mu$m & $0.30 \pm 0.04$ \\ % normalized \footnote{normalization procedure assumes appropriate beam chromaticity.} emittance $\epsilon_{n,x}$ & $\mu$m & $10.10 \pm 0.51$ \\ %normalized emittance $\epsilon_{n,y}$ & $\mu$m & $8.06 \pm 1.1$ \\ $\beta_x$-function & m & $1.40 \pm 0.06$ \\ $\beta_y$-function & m & $1.17 \pm 0.13$ \\ $\alpha_x$-function & rad & $0.97 \pm 0.06$ \\ $\alpha_y$-function & rad & $0.24 \pm 0.07$ \\ micro-pulse charge & pC & 11 \\ micro-pulse length & ps & 35 \\ energy of the beam $E$ & MeV & 15 $\pm$ 1.6 \\ relative energy spread $\Delta E/E$ & \% & 10.4 \\ \bottomrule \end{tabular} \label{tab:results} \end{table}
\section{Measurement of HRRL Electron Beam Energy \\Spread at 12~MeV}
The HRRL energy profile was measured when it was tuned to accelerate electrons to 12~MeV peak energy. A Faraday cup was placed at the end of the 45 degree beamline to measure the electron beam current when D1 was on and D2 was off. The dipole coil current for D1 was changed in 1~A increments. As the dipole coil current was changed, the energy of the electrons transported to the Faraday cup would change as described in Appendix A. Figure~\ref{fig:En-Scan} illustrates a measurement of the 12~MeV peak illustrating the observed low energy tail. The HRRL energy profile can be described by overlapping two skewed Gaussian fits~\cite{sup-Gau}. The fit function is given by \begin{equation} G(En)=A_{1}e^{\frac{-\left(En-\mu_{1}\right)^{2}}{2\left\{ \sigma_{1}\left[1+sgn\left(En-\mu_{1}\right)\right]\right\} ^{2}}}+A_{2}e^{\frac{-\left(En-\mu_{2}\right)^{2}}{2\left\{ \sigma_{2}\left[1+sgn\left(En-\mu_{2}\right)\right]\right\} ^{2}}}, \label{eq:skew-Gau} \end{equation} where $sgn$ is the sign function, that is defined as $$ sgn=\left\{ \begin{array}{ll}
\mbox -1\ & {(x<0)} \\
\mbox 0 \ & {(x=0)} \\
\mbox 1 \ & {(x>0)}.\\
\end{array}\right.
$$ The other variables are defined as $\sigma_{1}=\frac{\sigma_{r,1}+\sigma_{l,1}}{2}$, $\sigma_{2}=\frac{\sigma_{r,2}+\sigma_{l,2}}{2}$, $E_{1}=\frac{\sigma_{r,1}-\sigma_{l,1}}{\sigma_{r,1}+\sigma_{l,1}}$, and $E_{2}=\frac{\sigma_{r,2}-\sigma_{l,2}}{\sigma_{r,2}+\sigma_{l,2}}$. The measurement results and fits are shown in Figure~\ref{fig:En-Scan} and in Table~\ref{tab:En-Scan_resluts}. \begin{figure}[htbp] \centering \includegraphics[scale=0.50]{4-Experiment/Figures/En_Fit_Assym_Gau.eps} \caption{HRRL energy scan (dots) and fit (line) with two skewed Gaussian distribution.} \label{fig:En-Scan} \end{figure} \begin{table} \centering \caption{Fit Parameters for Two Skewed Gaussian.} \begin{tabular}{lclcc} \toprule {Parameter} & Notation & Unit & {First Gaussian} & {Second Gaussian} \\ \midrule amplitude & A & mA & ~2.14 & 10.88 \\ mean & $\mu$ & MeV & 12.07 & 12.32 \\ sigma left & $\sigma_L$ & MeV & ~4.47 & ~0.70 \\ sigma right & $\sigma_R$ & MeV & ~1.20 & ~0.45 \\ \bottomrule \end{tabular} \label{tab:En-Scan_resluts} \end{table}
% % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % \section{The Electron Beam Current Measurement}
A scintillator was placed between Q9 and Q10, as shown in Figure~\ref{fig:Scint_e-}, to monitor the electron beam current. The electron beam current was changed incrementally to measure the correlation between the scintillator and the accelerated electron beam. The beam current was measured using FC1 and the output was integrated using an oscilloscope. The scintillator output was integrated using an ADC (CAEN Mod. V792). As the electron beam current was decreased, the signal observed on the oscilloscope decreased and the ADC measured less charge from the scintillator as shown in Figure~\ref{fig:ADC-CH9}. A linear fit to data resulted a linear relation \begin{equation} Q_{\text{e}^-}(i) = (0.0186 \pm 0.0028)i + 2.79 \pm 0.08~\text{C}, \end{equation} where $i$ is ADC channel number and Q is the accelerated electron beam charge. The fit is shown in Figure~\ref{fig:calb-fit}.
\begin{figure}[htbp] \centering \includegraphics[scale=0.35]{4-Experiment/Figures/HRRL_line.eps} \caption{The electron beam monitor.} \label{fig:Scint_e-} \end{figure}
\begin{figure}[htbp] \centering \includegraphics[scale=0.80]{4-Experiment/Figures/ScintilatorCalibration/ADC_CHAN3.eps} \caption{The photon flux detected using scintillator. The mean of the ADC channel decreased linearly as the electron beam current was decreased.} \label{fig:ADC-CH9} \end{figure}
\begin{figure}[htbp] \centering \includegraphics[scale=0.50]{4-Experiment/Figures/ScintilatorCalibration/calb.eps} \caption{Fit for accelerator beam current $v.s.$ the ADC channel.} \label{fig:calb-fit} \end{figure}
\begin{table} \centering \caption{Scintillator Calibration Data.} \begin{tabular}{lll} \toprule {Run Number} & {Faraday Cup} & {Mean of ADC} \\ { } & {Charge Area (nVs)} & {Channel 9} \\ \midrule 3703 & $1201 \pm 10$ & $1126 \pm 0.8$ \\ 3705 & $777 \pm 110$ & $791.8 \pm 0.6$ \\ 3706 & $367.7 \pm 2.3$ & $242.1 \pm 0.3$ \\ \bottomrule \end{tabular} \label{tab:scint_calb} \end{table}
When running in coincidence mode, the electron beam current is sampled by the scintillator only when a coincidence event occurs causing a trigger that gates the ADC and measures the scintillator output for that positron coincidence event. The charge measured by the ADC is the total charge of the electron pulses that created the positron events. The number of beam pulses are counted using a scaler. The total charge on T1 for the entire run is estimated using \begin{equation} Q_{\text{C}} = \left ( \overset{N}{\underset{i}{\sum}} 0.0186i\times(\text{bin~content}[i]) + 2.79 \right ) \times \frac{\text{(\# of beam pulses)}}{\text{(\# of events)}}. \label{eq:q_calc1} \end{equation} \noindent
\section{Positron Rate Estimation in Coincidence Mode}
The background subtracted and normalized photon energy spectra observed using two NaI detectors for $3.00 \pm 0.07$~MeV are shown in Figure~\ref{fig:pos_NaILR}. Figure~\ref{fig:pos_NaILR} (a) and (b) are the background subtracted spectrum with no coincidence or energy cut. Figure~\ref{fig:pos_NaILR} (c) and (d) illustrate events observed in coincidence and within a energy window of $511\pm75$~keV for both detectors. The measured positron rate using NaI detectors in coincidence mode was 0.25~Hz for $3.00 \pm 0.07$~MeV positrons. %The uncertainty of the power supplies used for dipoles is 0.1~A which creates 0.06~MeV uncertainty in energy of the beam bent by dipoles. \begin{figure}[htbp] \centering \begin{tabular}{cc} {\scalebox{0.8} [0.80]{\includegraphics[scale=0.40]{4-Experiment/Figures/subtract/whole/NaI_L/r3735_sub_r3736.png}}} & {\scalebox{0.8} [0.80]{\includegraphics[scale=0.40]{4-Experiment/Figures/subtract/whole/NaI_R/r3735_sub_r3736.png}}} \\ (a) & (b) \\ & \\ & \\ {\scalebox{0.8} [0.8]{\includegraphics[scale=0.40]{4-Experiment/Figures/subtract/511_peak/NaI_L/r3735_sub_r3736.png}}} & {\scalebox{0.8} [0.8]{\includegraphics[scale=0.40]{4-Experiment/Figures/subtract/511_peak/NaI_R/r3735_sub_r3736.png}}} \\ (c) & (d) \\
& \\
\end{tabular} \caption{Photon spectrum of NaI detectors after background subtraction created by 3~MeV positrons incident on T2. (a) and (b) are spectrum after background subtractions. (c) and (d) are the spectrum of events coincident in both detectors in 511~keV peaks.} \label{fig:pos_NaILR} \end{figure}
%The electron beam was transported to a phosphorous screen at the end of the 90 degree beamline to find the errors on the positron beam energy. The positron beam current was too low to be observed on phosphorous screen. %The beam centered on the phosphorous screen and then steered to the edge by changing current of D2 by 0.1~A. %The phosphorous screen is twice as large as T2 in horizantal direction.
\section{The Positron Production Runs} The annihilation target T2 is insertable into the beamline and placed inside a 6-way cross that has horizontal sides vacuum sealed with 1~mil stainless steel windows. Positrons intercepting T2 thermalise, annihilate, and produce 511~keV photon pairs back-to-back. These photons are detected by two NaI detectors facing T2 and shielded with Pb bricks as shown in Figure~\ref{fig:HRRL-En-Scan}. The background was measured by retracting T2 thereby allowing positrons to exit the beamline and be absorbed by the beam dump.
\begin{figure}[htbp] \centering \includegraphics[scale=0.50]{4-Experiment/Figures/PositronDetection/NaI_Setup4.png} \caption{Positron detection using T2 and NaI detectors.} \label{fig:HRRL-En-Scan} \end{figure}
As shown in Figure~\ref{fig:Dipole-in}, a 511~keV peak was observed (solid line) when T2 was in. A permanent dipole magnet was placed on the beamline after Q10 to deflect charged particles on the accelerator side preventing them from entering the shielded cell. The peak was not observed (dashed line) when T2 was in and the permanent magnet was used. The peak was also not observed (doted dashed line) when T2 and the permanent magnet were removed. Thus, one may argue that the observed peak is due to positrons annihilating in T2.
\begin{figure}[htbp] \centering \begin{tabular}{cc} {\scalebox{0.35} [0.35]{\includegraphics{4-Experiment/Figures/SweepingDipole/LNaI3.png}}} & {\scalebox{0.35} [0.35]{\includegraphics{4-Experiment/Figures/SweepingDipole/RNaI3.png}}} \\ (a) Original spectrum on left NaI. & (b) Original spectrum on right NaI.\\ \end{tabular} \caption{Photon spectrum when a permanent dipole magnet is inserted along with T2 (dashed line), dipole out and T2 in (solid line), and dipole removed and T2 out (dotted dashed line). The positron energy incident on the T2 was $2.15\pm0.06$~MeV.} \label{fig:Dipole-in} \end{figure}
The normalized photon energy spectra observed by two NaI detectors are shown in Figure~\ref{fig:in-out-runs} when T2 was both in (signal) and out (background) of the beamline. Figure~\ref{fig:in-out-runs} (c) and (d) illustrate the events observed when 511~keV photons were required in both detectors. The signal is indicated by the solid line and background by dashed line.
\begin{figure}[htbp] \centering \begin{tabular}{cc} {\scalebox{0.315} [0.315]{\includegraphics{4-Experiment/Figures/NaI_L1/r3735_sub_r3736_2.png}}} & {\scalebox{0.315} [0.315]{\includegraphics{4-Experiment/Figures/NaI_R1/r3735_sub_r3736_2.png}}} \\ (a) Original spectrum on left NaI. & (b) Original spectrum on right NaI.\\ & \\ & \\ {\scalebox{0.315} [0.315]{\includegraphics{4-Experiment/Figures/NaI_L2/r3735_sub_r3736_2.png}}} & {\scalebox{0.315} [0.315]{\includegraphics{4-Experiment/Figures/NaI_R2/r3735_sub_r3736_2.png}}} \\
(c) Spectrum with cut on left NaI. & (d) Spectrum with cut on right NaI.\\ & \\ \end{tabular} \caption{The time normalized spectra of photons created by 3~MeV positrons incident on T2. In the top row are original spectrum and in the bottom row are spectrum of incidents happened in the 511~keV peak coincidently in both detectors. The positron beam energy incident on the T2 was $3.00\pm0.06$~MeV.} \label{fig:in-out-runs} \end{figure}
%\begin{table} %\centering %\caption{Run Parameters of The Run No. 3735.} %\begin{tabular}{lll} %\toprule %{Parameter} & {Unit} & {Value} \\ %\midrule %run number & & 3735 \\ %repetition rate & Hz & 300 \\ %run time & s & 1002 \\ %pulses & & 301462 \\ %events & & 9045 \\ %e$^+$ Counts on NaI Detectors & & 256 $\pm$ 16\\ %\bottomrule %\end{tabular} %\label{tab:run3735} %\end{table}
\section{Positron Rate Estimation in OR Mode}
The positron rate was also measured by running NaI detectors in OR mode and the photon spectrum are shown in Figure~\ref{fig:Or-mode} for $2.15 \pm 0.06$~MeV positrons incident on T2. The rate was $0.21$~Hz for left and $0.35$~Hz right NaI detectors in OR mode while the rate in coincidence (AND) mode was $0.028$~Hz.
\begin{figure}[htbp] \centering \begin{tabular}{cc} {\scalebox{0.8} [0.80]{\includegraphics[scale=0.40]{4-Experiment/Figures/NaIOrMode/r3679_sub_r3680_NaI_L.png}}} & {\scalebox{0.8} [0.80]{\includegraphics[scale=0.40]{4-Experiment/Figures/NaIOrMode/r3679_sub_r3680_NaI_R.png}}} \\ (a) Left NaI detector.& (b) Right NaI detector.\\ & \\ \end{tabular} \caption{The photon rates for $2.15 \pm 0.06$~MeV incident positrons measured by running NaI detectors in OR mode. The rate was $0.21$~Hz for left and $0.35$~Hz right NaI detectors in OR mode while the rate in coincidence (AND) mode was $0.028$~Hz.} \label{fig:Or-mode} \end{figure}
\section{Positron to Electron Ratio} The ratios of positrons detected using NaI detectors in coincidence mode to the electrons impinging on T1 at different energies are given in Table~\ref{tab:e+2e-} and Figure~\ref{fig:e+2e-}. A simulation was used to estimate the systematic error of the positrons at different energies. The ratio errors are calculated by propagating the statistical errors of positron and electron rates. %error on total counts = sqt(total counts). Rate = Counts/time. Error on rates = sqrt(d(rate)/d(counts)^2*(error on the counts)^2)=sqrt((error on the counts)^2/time^2)=sqrt(counts/time^2)=sqrt(rate/time). \begin{table} \centering \caption{Positron to Electron Rate Ratio.} \begin{tabular}{ccc} \toprule {Energy} & {Positron to Electron Ratio} & {Systematic Error} \\ \midrule $1.02 \pm 0.03$ & $(0.19 \pm 0.19)\times10^{-16}$ & 57.3 \% \\ $2.15 \pm 0.06$ & $(0.69 \pm 0.24)\times10^{-16}$ & 5.8 \% \\ $3.00 \pm 0.07$ & $(8.25 \pm 0.96)\times10^{-15}$ & 2.7 \% \\ $4.02 \pm 0.07$ & $(4.20 \pm 0.80)\times10^{-15}$ & 2.7 \% \\ $5.00 \pm 0.06$ & $(0.62 \pm 0.16)\times10^{-16}$ & 6.7 \% \\
\bottomrule \end{tabular} \label{tab:e+2e-} \end{table} \begin{figure}[htbp] \centering \includegraphics[scale=0.72]{4-Experiment/Figures/Ratio/R.eps} \caption{The ratios of positrons detected by NaI detectors in coincidence mode to the electrons impinging T1.} \label{fig:e+2e-} \end{figure}
%\subsubsection{Error on Ratio} % %Error on electron beam is derived from: % %Error on positron beam rate is derived from: $\sqrt{\frac{positron~rate}{run~time}}$ % %\subsubsection{Annihilation Target Angle} %Use simulation to determine how sensitive annihilation of positrons is to angle. % %What is the dependence of the annihilation target angle with the probability of a positron annihilating in the target and producing a photon that is detected by the NaI detector, % %What is the distribution of 511s as a function of angle phi when theta is 90 degrees? Are they uniformly produced? %\subsubsection{Energy cut systematics} % %How does the positron production efficiency change when you change the range of the 511 cut.
Conclusions and Suggestions
\chapter{Conclusions and Suggestions} A new High Repetition Rate Linac (HRRL) beamline has been successfully reconfigured to produce and transport positrons to the experimental cell. The electron beam energy profile and emittance of the HRRL were measured using a Faraday cup and an OTR based diagnostic system. Positrons generated when the electron beam impinged on a tungsten target (T1) were transported to another tungsten target, T2. The 511~keV photons created inside T2 by the annihilated positrons were detected using two NaI detectors. The positron beam creation, beam loss in the transportation, and detection process were studied using the simulation package G4beamline and compared to this experiment. %The simulation package G4beamline compared to this experiment
An OTR based diagnostic tool was designed, constructed, and used to measure the beam emittance of the HRRL. The electron spatial profile measured using the OTR system was not described by a Gaussian distribution but by a super Gaussian or Lorentzian distribution. The projected emittances of the HRRL were measured to be less than 0.4~$\mu$m by the OTR based tool using the quadrupole scanning method when accelerating electrons to an energy of 15~MeV. %OTR used, Not Guassian, Changed magnet, measured emttiance
The positron detection system was constructed using two NaI detectors and a 1.016~mm thick retractable tungsten target placed in the 6-way cross. Positrons were measured at energies between 1 and 5~MeV as illustrated by the hollow diamond symbols in Figure~\ref{fig:e+2e-exp-sim}. The ratio of positrons detected on NaI detectors to electrons incident on T1 is on the order of $10^{-15}$. The ratio is the highest near 3~MeV. %In the experiment, quadrapoles were optimized to only transport 2~MeV and due to the limited beam time and it could have diminished transportation efficiency for other energies. %Further experimental study is necessary to investigate the positron beam energy distribution. % as illustrated by hallow diamond symbal in Figure. The simulation shown in Figure~\ref{fig:e+2e-exp-sim} predicts the positron production efficiency for the energies measured in this experiment. The simulation includes the measured initial electron energy profile, beam losses during transportation, annihilation in T2, and detection efficiencies. While the simulation result agrees with the experiment in that the peak energy distribution is near 3~MeV, it predicts a higher positron to electron ratio as shown in Figure~\ref{fig:e+2e-exp-sim}. %Beam loss
The ratio of the positrons contained within the beampipe to the 511~keV photons detected in coincidence mode when the dipoles were set to bend 3~MeV positrons is predicted to be 1655:1 by the simulation. The ratio of the positrons on T2 to the 511~keV photons is 620:1 under the same conditions as above.
The 3~MeV positron rate measured in experiment was 0.25~Hz when the HRRL was operated at a 300~Hz repetition rate, 100~mA peak current, and 300~ns (FWHM) RF macro pulse length.
Based on this simulation, a measured 0.25~Hz coincidence rate by the NaI detectors would correspond to a 155~Hz positron rate incident on T2.
The observed positron to electron ratio was insensitive to the quadrupole triplet collection field setting. Section 3.5 indicates that the solid angle subtended by the quad entrance window approximated the positron loss.
Since positrons have a larger angular distribution, perhaps a solenoid may be a better option to improve the collection efficiency.
Positioning the target T1 at the entrance of quad or solenoid may be the optimal choice for capturing positrons.
%7. Experimental results show quadrupole magnets are not efficient in collecting positrons, since positrons have large angular distribution. Solenoid might be able to improve the collection efficiency of positrons~\cite{kim-bindu-solenoid} and should be placed as close the production target as possible for better efficiency.
\begin{figure}[htbp] \centering \includegraphics[scale=0.75]{5-Conclusion/Figures/Overlay_Exp-Sim-Ratio/R1.eps} \caption{Ratio of positrons detected to electrons measured in the experiment (hollow diamond) and simulation (full circle).} \label{fig:e+2e-exp-sim} \end{figure}
List of Figures
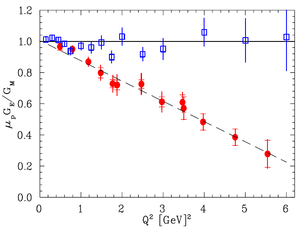 1.1 Form factor ratio, obtained by Rosenbluth Technique (hollow square) and results from Recoil Polarization Technique [5]. . . . . 3
1.1 Form factor ratio, obtained by Rosenbluth Technique (hollow square) and results from Recoil Polarization Technique [5]. . . . . 3
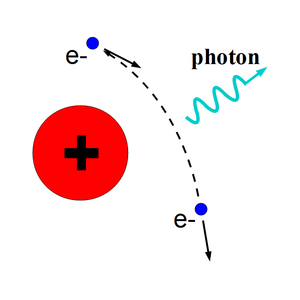 1.2 Photon generation from Bremsstrahlung processes. . . . . . . . . . . . . . . 4
1.2 Photon generation from Bremsstrahlung processes. . . . . . . . . . . . . . . 4
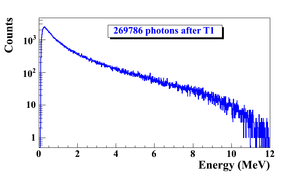 1.3 Simulated Bremsstrahlung photon energy right after a tungsten foil. . . . . . 5
1.3 Simulated Bremsstrahlung photon energy right after a tungsten foil. . . . . . 5
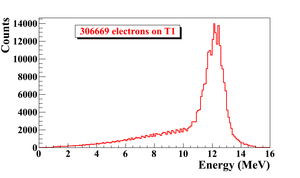 1.4 Simulated electron energy distribution right before a tungsten foil. . . . . . . 6
1.4 Simulated electron energy distribution right before a tungsten foil. . . . . . . 6
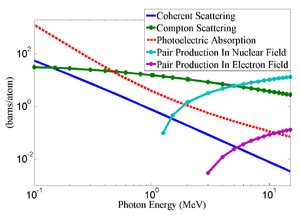 1.5 Cross section for each type of photon interaction with tungsten as function of photon energy [10]. . . . . . . . . . . . . . . . 6
1.5 Cross section for each type of photon interaction with tungsten as function of photon energy [10]. . . . . . . . . . . . . . . . 6
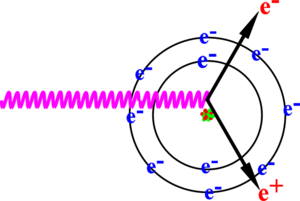 1.6 Pair production. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.6 Pair production. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
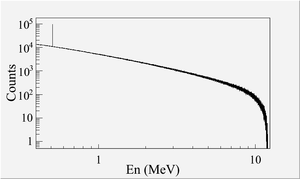 1.7 Photon spectrum of 12 MeV mono energy 10 million electrons impinge on a 1.016 mm thick tungsten target. . . . . . . . . . . 8
1.7 Photon spectrum of 12 MeV mono energy 10 million electrons impinge on a 1.016 mm thick tungsten target. . . . . . . . . . . 8
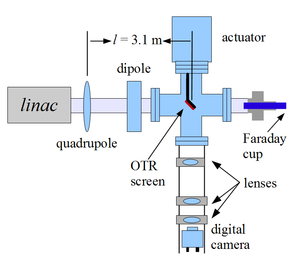 1.8 Apparatus used to measure the beam emittance. . . . . . . . . . . . . . . . . 11
1.8 Apparatus used to measure the beam emittance. . . . . . . . . . . . . . . . . 11
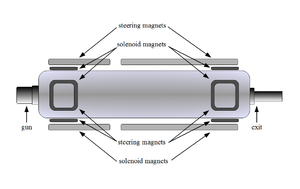 2.1 HRRL cavity. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.1 HRRL cavity. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
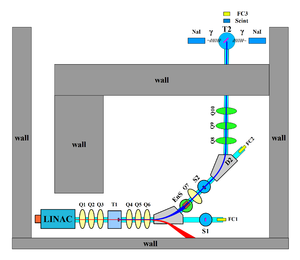 2.2 HRRL beamline layout and parts. . . . . . . . . . . . . . . . . . . . . . . . . 17
2.2 HRRL beamline layout and parts. . . . . . . . . . . . . . . . . . . . . . . . . 17
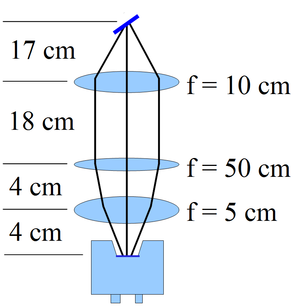
 2.3 The OTR Imaging system. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.3 The OTR Imaging system. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
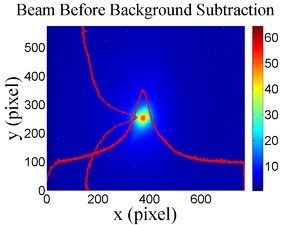
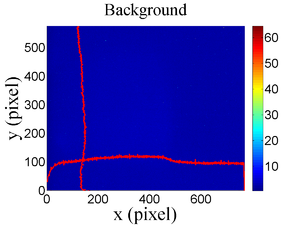
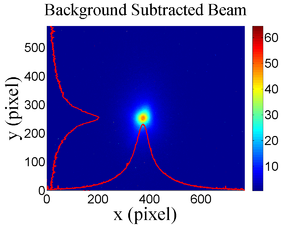 2.4 Background subtracted to minimize impact of dark current; (a) a beam with the dark current and background noise, (b) a background image, (c) a beam
image when dark background was subtracted. . . . . . . . . . . . . . . . . . 21
2.4 Background subtracted to minimize impact of dark current; (a) a beam with the dark current and background noise, (b) a background image, (c) a beam
image when dark background was subtracted. . . . . . . . . . . . . . . . . . 21
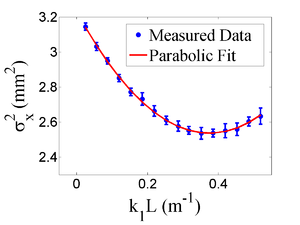
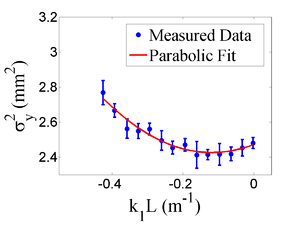 2.5 Square of rms values and parabolic fittings. . . . . . . . . . . . . . . . . . . . 23
2.5 Square of rms values and parabolic fittings. . . . . . . . . . . . . . . . . . . . 23
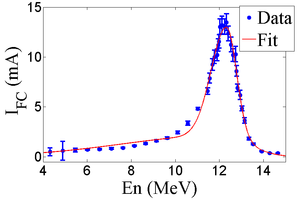 2.6 HRRL energy scan (blue dots) and fit (red line) with two skewed Gaussian distribution. . . . . . . . . . . . . . . 25
2.6 HRRL energy scan (blue dots) and fit (red line) with two skewed Gaussian distribution. . . . . . . . . . . . . . . 25
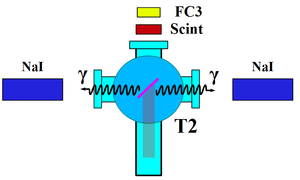 2.7 Positron Detection System. T2 (pink) is 45 degree placed with horizontal plane, then rotated towards left detector 45 degree. . . . . . . . . . . 26
2.7 Positron Detection System. T2 (pink) is 45 degree placed with horizontal plane, then rotated towards left detector 45 degree. . . . . . . . . . . 26
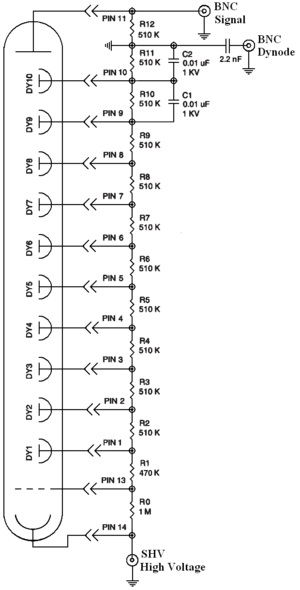 2.8 Modified PMT base design. . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.8 Modified PMT base design. . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
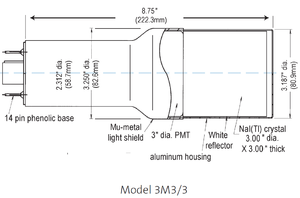 2.9 NaI crystal dimension. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.9 NaI crystal dimension. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
 2.10 NaI crystals and new bases. . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.10 NaI crystals and new bases. . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
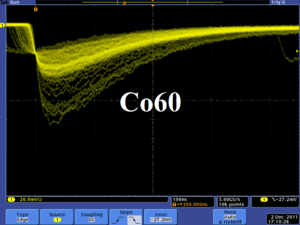 2.11 Pulses from Co-60 source observed on the scope. The amplitude is about 60 mV. The rise time is larger than 50 ns, and the fall time is larger than 700 ns. . . . . . . . .. . . . . . . . . 30
2.11 Pulses from Co-60 source observed on the scope. The amplitude is about 60 mV. The rise time is larger than 50 ns, and the fall time is larger than 700 ns. . . . . . . . .. . . . . . . . . 30
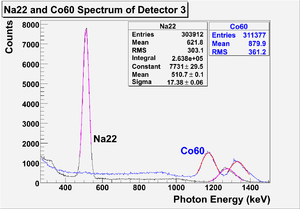 2.12 Calibrated NaI spectrum of Na-22 and Co-60 sources. . . . . . . . . . . . . . 30
2.12 Calibrated NaI spectrum of Na-22 and Co-60 sources. . . . . . . . . . . . . . 30
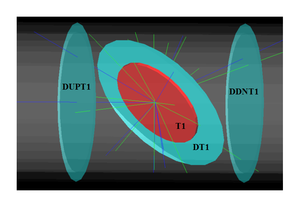 3.1 T1 is positron production target with same geometry and material as real target. DUPT1 is virtual detector located upstream to sample incoming electron
beam. DDNT1 is down stream virtual detector; DT1 is a virtual detector that is placed right after T1 with same angle as T1. . . . . . . . . 34
3.1 T1 is positron production target with same geometry and material as real target. DUPT1 is virtual detector located upstream to sample incoming electron
beam. DDNT1 is down stream virtual detector; DT1 is a virtual detector that is placed right after T1 with same angle as T1. . . . . . . . . 34
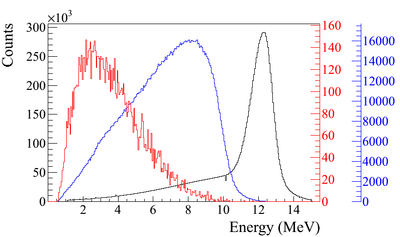 3.2 Energy distribution of positrons detected on virtual detector DDNT1. . . . . 35
3.2 Energy distribution of positrons detected on virtual detector DDNT1. . . . . 35
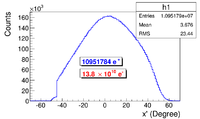
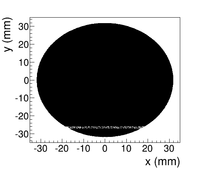
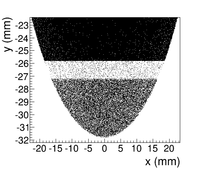 3.3 Transverse spacial and angular distribution of positrons on the virtual detector DDNT1. . . . . . . . . . 36
3.3 Transverse spacial and angular distribution of positrons on the virtual detector DDNT1. . . . . . . . . . 36
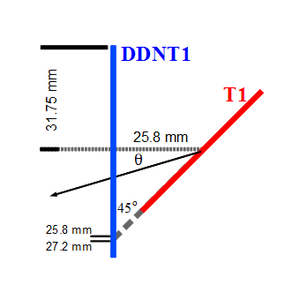 3.4 Geometry of the target T1 and the virtual detector DDNT1. . . . . . . . . . 37
3.4 Geometry of the target T1 and the virtual detector DDNT1. . . . . . . . . . 37
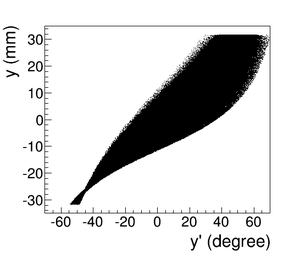
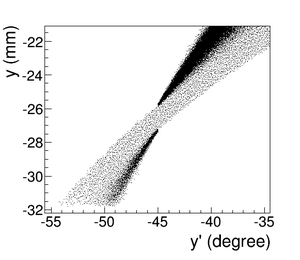 3.5 Positron beam distribution Y divergence vs. Y spacial distribution on DDNT1. 37
3.5 Positron beam distribution Y divergence vs. Y spacial distribution on DDNT1. 37
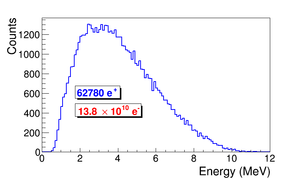 300 px
3.6 Positron beam energy distribution detected on the downstream of T2. . . . . 38
300 px
3.6 Positron beam energy distribution detected on the downstream of T2. . . . . 38
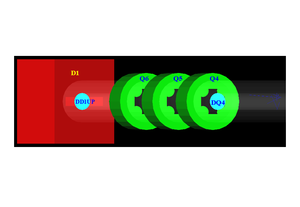 3.7 Step 2 setup. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.7 Step 2 setup. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
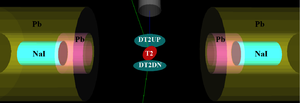 3.8 T2 and virtual detectors located upstream (DT2UP) and downstream (DT2DN) of T2. NaI dettectos and Pb shielding. . . . . . . . . . . 40
3.8 T2 and virtual detectors located upstream (DT2UP) and downstream (DT2DN) of T2. NaI dettectos and Pb shielding. . . . . . . . . . . 40
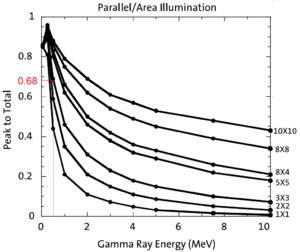 3.9 NaI detector eficiency [21]. . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.9 NaI detector eficiency [21]. . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
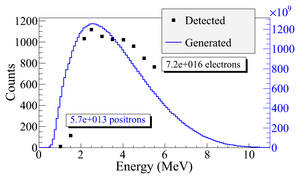 3.10 Positrons generated detected on virtual detector DDNT1 and 511 keV counts
detected by NaI detectors in coincidence mode (100 % eficiency assumed). . 42
3.10 Positrons generated detected on virtual detector DDNT1 and 511 keV counts
detected by NaI detectors in coincidence mode (100 % eficiency assumed). . 42
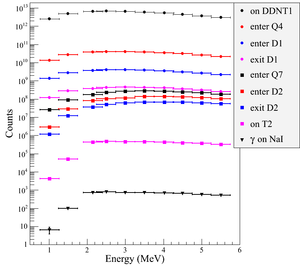 3.11 Predicted number positrons of transported. Black circle: positrons after T1. Red circle: positrons enter Q4. Blue circle: positrons enters D1. Magenta
circle: positrons reaches T2. . . . . . . . . . . . . . . .. . . 42
3.11 Predicted number positrons of transported. Black circle: positrons after T1. Red circle: positrons enter Q4. Blue circle: positrons enters D1. Magenta
circle: positrons reaches T2. . . . . . . . . . . . . . . .. . . 42
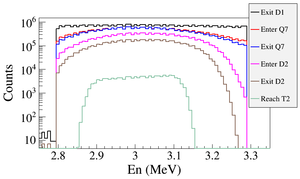 3.12 Beam transported when dipoles are set for 3 MeV positrons. . . . . . . . . . 45
3.12 Beam transported when dipoles are set for 3 MeV positrons. . . . . . . . . . 45
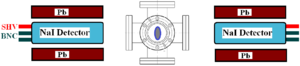 4.1 Positron detection using T2 and NaI detectors. . . . . . . . . . . . . . . . . . 49
4.1 Positron detection using T2 and NaI detectors. . . . . . . . . . . . . . . . . . 49
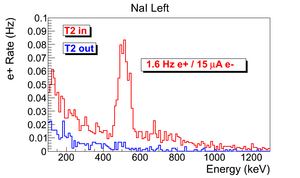
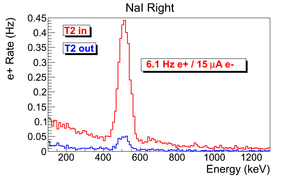
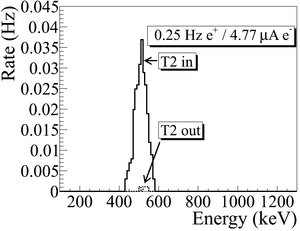
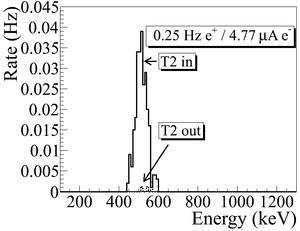 4.2 T2 in run (red) and T2 out background run (blue) time normalized spectrum. Top row shows original spectrum and bottom row shows incidents only happen
in 511 keV peak coincidently on both detectors. . . . . . . . . . . . 50
4.2 T2 in run (red) and T2 out background run (blue) time normalized spectrum. Top row shows original spectrum and bottom row shows incidents only happen
in 511 keV peak coincidently on both detectors. . . . . . . . . . . . 50
 4.3 Electron beam monitor. . . . . . . . . . . . . . . . . .. . . . 52
4.3 Electron beam monitor. . . . . . . . . . . . . . . . . .. . . . 52
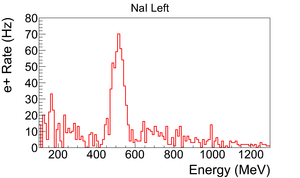
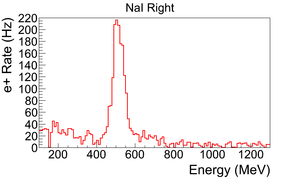
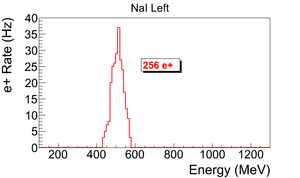
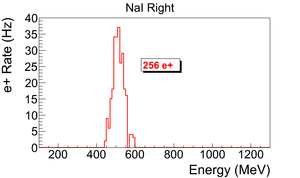 4.4 Electron beam monitor ADC signal . . . . . . . . . . . . . . . . . . . . . . . 52
4.4 Electron beam monitor ADC signal . . . . . . . . . . . . . . . . . . . . . . . 52
 4.5 Ratio of positrons detected to electrons in experiment. . . . . . . . . . . . . 55
4.5 Ratio of positrons detected to electrons in experiment. . . . . . . . . . . . . 55
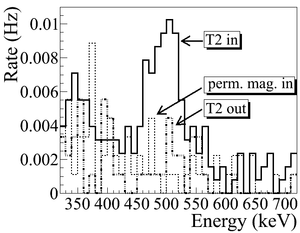
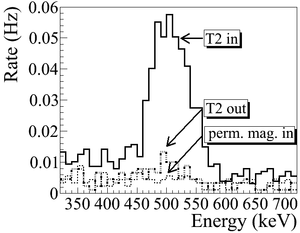 Photon spectrum when permanent dipole magnet in and T2 in (dashed line), dipole out and T2 in (bold dashed line), and dipole in and T2 out (solid line). The positron energy incident on the T2 was $2.15\pm0.06$~MeV.
Photon spectrum when permanent dipole magnet in and T2 in (dashed line), dipole out and T2 in (bold dashed line), and dipole in and T2 out (solid line). The positron energy incident on the T2 was $2.15\pm0.06$~MeV.
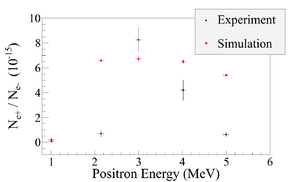 5.1 Ratio of positrons detected to electrons in experiment and simulation. . . . . 58
5.1 Ratio of positrons detected to electrons in experiment and simulation. . . . . 58