TF ErrorAnalysis WIP

Hypothesis testing distributions

t-Distribution

The Student's t-distribution is defined as

[math]t = \frac{\bar{x} - \mu}{s/\sqrt{N}}[/math]

t-distribution is a "one tailed" test typically used for small sample sizes (N > 24) where the parent population mean [math]\mu[/math] is known.

F-distribution

[math]F= \frac{s_1^2}{s_2^2}[/math]

For this class we shall define a hypothesis test as a test used to

There are two schools of thought on this

Chi-Square

P-value

Root fundtion to evaluate meaning of Chi-square

PDG => Rather, the p-value is the probability, under the assumption of a hypothesis H , of obtaining data at least as incompatible with H as the data actually observed.

From http://en.wikipedia.org/wiki/P-value and http://en.wikipedia.org/wiki/Statistical_significance

the p-value is the frequency or probability with which the observed event would occur, if the null hypothesis were true. If the obtained p-value is smaller than the significance level, then the null hypothesis is rejected.

In some fields, for example nuclear and particle physics, it is common to express statistical significance in units of "σ" (sigma), the standard deviation of a Gaussian distribution. A statistical significance of "[math]n\sigma[/math]" can be converted into a value of α via use of the error function:

[math]\alpha = 1 - \operatorname{erf}(n/\sqrt{2}) \, [/math]

The use of σ is motivated by the ubiquitous emergence of the Gaussian distribution in measurement uncertainties. For example, if a theory predicts a parameter to have a value of, say, 100, and one measures the parameter to be 109 ± 3, then one might report the measurement as a "3σ deviation" from the theoretical prediction. In terms of α, this statement is equivalent to saying that "assuming the theory is true, the likelihood of obtaining the experimental result by coincidence is 0.27%" (since 1 − erf(3/√2) = 0.0027).

What is a p-value?

A p-value is a measure of how much evidence we have against the null hypothesis. The null hypothesis, traditionally represented by the symbol H0, represents the hypothesis of no change or no effect.

The smaller the p-value, the more evidence we have against H0. It is also a measure of how likely we are to get a certain sample result or a result “more extreme,” assuming H0 is true. The type of hypothesis (right tailed, left tailed or two tailed) will determine what “more extreme” means.

Much research involves making a hypothesis and then collecting data to test that hypothesis. In particular, researchers will set up a null hypothesis, a hypothesis that presumes no change or no effect of a treatment. Then these researchers will collect data and measure the consistency of this data with the null hypothesis.

The p-value measures consistency by calculating the probability of observing the results from your sample of data or a sample with results more extreme, assuming the null hypothesis is true. The smaller the p-value, the greater the inconsistency.

Traditionally, researchers will reject a hypothesis if the p-value is less than 0.05. Sometimes, though, researchers will use a stricter cut-off (e.g., 0.01) or a more liberal cut-off (e.g., 0.10). The general rule is that a small p-value is evidence against the null hypothesis while a large p-value means little or no evidence against the null hypothesis. Please note that little or no evidence against the null hypothesis is not the same as a lot of evidence for the null hypothesis.

It is easiest to understand the p-value in a data set that is already at an extreme. Suppose that a drug company alleges that only 50% of all patients who take a certain drug will have an adverse event of some kind. You believe that the adverse event rate is much higher. In a sample of 12 patients, all twelve have an adverse event.

The data supports your belief because it is inconsistent with the assumption of a 50% adverse event rate. It would be like flipping a coin 12 times and getting heads each time.

The p-value, the probability of getting a sample result of 12 adverse events in 12 patients assuming that the adverse event rate is 50%, is a measure of this inconsistency. The p-value, 0.000244, is small enough that we would reject the hypothesis that the adverse event rate was only 50%.

A large p-value should not automatically be construed as evidence in support of the null hypothesis. Perhaps the failure to reject the null hypothesis was caused by an inadequate sample size. When you see a large p-value in a research study, you should also look for one of two things:

a power calculation that confirms that the sample size in that study was adequate for detecting a clinically relevant difference; and/or a confidence interval that lies entirely within the range of clinical indifference. You should also be cautious about a small p-value, but for different reasons. In some situations, the sample size is so large that even differences that are trivial from a medical perspective can still achieve statistical significance.

As a statistician, I am not in a good position to advise you on whether a difference is trivial or not. As a medical expert, you need to balance the cost and side effects of a treatment against the benefits that the therapy provides.

The authors of the research paper should inform you what size difference is clinically relevant and what sized difference is trivial. But if they don't, you should. Ask yourself how much of a difference would be large enough to cause you to change your practice. Then compare this to the confidence interval in the research paper. If both limits of the confidence interval are smaller than a clinically relevant difference, then you should not change your practice, no matter what the p-value tells you.

You should not interpret the p-value as the probability that the null hypothesis is true. Such an interpretation is problematic because a hypothesis is not a random event that can have a probability.

Bayesian statistics provides an alternative framework that allows you to assign probabilities to hypotheses and to modify these probabilities on the basis of the data that you collect.

Example

A large number of p-values appear in a publication

Consultation Patterns and Provision of Contraception in General Practice Before Teenage Pregnancy: Case-Control Study. Churchill D, Allen J, Pringle M, Hippisley-Cox J, Ebdon D, Macpherson M, Bradley S. British Medical Journal 2000: 321(7259); 486-9. [Abstract] [Full text] [PDF]

by Churchill et al 2000. This was a study of consultation practices among teenagers who become pregnant. The researchers selected 240 patients (cases) with a recorded conception before the age of 20. Three controls were selected for each case and were matched on age and practice.

The not too surprising finding is that the cases were more likely to have consulted certain health professionals in the year before conception and were more likely to request contraceptive protection. This demonstrates that teenagers are not reluctant to seek advice about contraception.

For example, 91% of the cases (219/240) sought the advice of a general practitioner in the year before conception compared to 82% of the controls (586/719) during a similar time frame. This is a large difference. The odds ratio is 2.37. The p-value is 0.001, which indicates that this ratio is statistically significantly different from 1.0. The 95% confidence interval for the odds ratio is 1.45 to 3.86.

In contrast, 23% of the cases (56/240) sought advice from a practice nurse while 24% of the controls (170/719) sought advice. This is a small difference and the odds ratio is 0.98. The p-value is 0.905, which indicates that this odds ratio does not differ significantly from 1. As with any negative finding, you should be concerned about whether the result is due to an inadequate sample size. The confidence interval, however, is 0.69 to 1.39. This indicates that the research study had a good amount of precision and that the sample size was reasonable.

root [3] TMath::Prob(1.31,11)

Double_t Prob(Double_t chi2, Int_t ndf)
 Computation of the probability for a certain Chi-squared (chi2)
 and number of degrees of freedom (ndf).

 Calculations are based on the incomplete gamma function P(a,x),
 where a=ndf/2 and x=chi2/2.

 P(a,x) represents the probability that the observed Chi-squared
 for a correct model should be less than the value chi2.

 The returned probability corresponds to 1-P(a,x),
 which denotes the probability that an observed Chi-squared exceeds
 the value chi2 by chance, even for a correct model.

--- NvE 14-nov-1998 UU-SAP Utrecht

Komolgorov test

http://en.wikipedia.org/wiki/Kolmogorov-Smirnov_test

References

1.) "Data Reduction and Error Analysis for the Physical Sciences", Philip R. Bevington, ISBN-10: 0079112439, ISBN-13: 9780079112439

CPP programs for Bevington

Bevington programs

2.)An Introduction to Error Analysis, John R. Taylor ISBN 978-0-935702-75-0

3.) ROOT: An Analysis Framework

4.) Orear, "Notes on Statistics for Physicists"

5.) Statistical Methods for Engineers and Scientists, Robert M. Bethea, Benjamin S. Duran, and Thomas L. Boullion, Marcel Dekker Inc, New York, (1985), QA 276.B425

6.) Data Analysis for Scientists and Engineers, Stuart L. Meyer, John Wiley & Sons Inc, New York, (1975), QA 276.M437

ROOT comands

A ROOT Primer

Download

You can usually download the ROOT software for multiple platforms for free at the URL below

http://root.cern.ch

There is a lot of documentation which may be reached through the above URL as well

Setup the environment

There is an environmental variable which is usually needed on most platforms in order to run ROOT. I will just give the commands for setting things up under the bash shell running on the UNIX platform.

Set the variable ROOTSYS to point to the directory used to install ROOT

export ROOTSYS=~/src/ROOT/root

I have installed the latest version of ROOT in the subdirectory ~/src/ROOT/root.

You can now run the program from any subdirectory with the command

$ROOTSYS/bin/root

If you want to compile programs which use ROOT libraries you should probably put the "bin" subdirectory under ROOTSYS in your path as well as define a variable pointing to the subdirectory used to store all the ROOT libraries (usually $ROOTSYS/lib).

PATH=$PATH:$ROOTSYS/bin

export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$ROOTSYS/lib

Other UNIX shell and operating systems will have different syntax for doing the same thing.

Starting and exiting ROOT

Starting and exiting the ROOT program may be the next important thing to learn.

As already mentioned above you can start ROOT by executing the command

$ROOTSYS/bin/root

from an operating system command shell. You will see a "splash" screen appear and go away after a few seconds. Your command shell is now a ROOT command interpreter known as CINT which has the command prompt "root[0]". You can type commands within this environment such as the command below to exit the ROOT program.

To EXIT the program just type

.q

Starting the ROOT Browser (GUI)

By now most computer users are accustomed to Graphical User Interfaces (GUIs) for application. You can launch a GUI from within the ROOT command interpreter interface with the command

new TBrowser();

A window should open with pull down menus. You can now exit root by selecting "Quit ROOT" from the pull down menu labeled "File" in the upper left part of the GUI window.

plotting Probability Distributions in ROOT

http://project-mathlibs.web.cern.ch/project-mathlibs/sw/html/group__PdfFunc.html

The Binomial distribution is plotted below for the case of flipping a coin 60 times (n=60,p=1/2)

You can see the integral , Mean and , RMS by right clicking on the Statistics box and choosing "SetOptStat". A menu box pops up and you enter the binary code "1001111" (without the quotes).

root [0] Int_t i;                                                                 
root [1] Double_t x                                                               
root [2] TH1F *B30=new TH1F("B30","B30",100,0,100)                                
root [3] for(i=0;i<100;i++) {x=ROOT::Math::binomial_pdf(i,0.5,60);B30->Fill(i,x);}
root [4] B30->Draw();                                                             

You can continue creating plots of the various distributions with the commands

root [2] TH1F *P30=new TH1F("P30","P30",100,0,100)                                
root [3] for(i=0;i<100;i++) {x=ROOT::Math::poisson_pdf(i,30);P30->Fill(i,x);}
root [4] P30->Draw("same");                                                             
root [2] TH1F *G30=new TH1F("G30","G30",100,0,100)                                
root [3] for(i=0;i<100;i++) {x=ROOT::Math::gaussian_pdf(i,3.8729,30);G30->Fill(i,x);}
root [4] G30->Draw("same");                                                             

The above commands created the plot below.

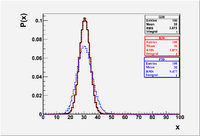File:Forest EA BinPosGaus Mean30.eps

Note

I set each distribution to correspond to a mean ([math]\mu[/math]) of 30. The [math]\sigma^2[/math] of the Binomial distribution is [math]np(1-p)[/math] = 60(1/2)(1/2) = 15. The [math]\sigma^2[/math] of the Poisson distribution is defined to equal the mean [math]\mu=30[/math]. I intentionally set the mean and sigma of the Gaussian to agree with the Binomial. As you can see the Binomial and Gaussian lay on top of each other while the Poisson is wider. The Gaussian will lay on top of the Poisson if you change its [math]\sigma[/math] to 5.477

for(i=0;i<100;i++) {x=ROOT::Math::gaussian_pdf(i,5.477,30);G30->Fill(i,x);}

Also Note

The Gaussian distribution can be used to represent the Binomial and Poisson distributions when the average is large ( ie:[math]\mu \gt 10[/math]). The Poisson distribution, though, is an approximation to the Binomial distribution for the special case where the average number of successes is small ( [math]\mu \lt \lt n[/math] because [math]p \lt \lt 1[/math])

Int_t i;                                                                 
Double_t x                                                               
TH1F *B30=new TH1F("B30","B30",100,0,10);
TH1F *P30=new TH1F("P30","P30",100,0,10);
for(i=0;i<10;i++) {x=ROOT::Math::binomial_pdf(i,0.1,10);B30->Fill(i,x);}
for(i=0;i<10;i++) {x=ROOT::Math::poisson_pdf(i,1);P30->Fill(i,x);}

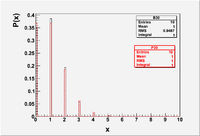File:Forest EA BinPos Mean1.eps

Other probability distribution functions

double	beta_pdf(double x, double a, double b)
double	binomial_pdf(unsigned int k, double p, unsigned int n)
double	breitwigner_pdf(double x, double gamma, double x0 = 0)
double	cauchy_pdf(double x, double b = 1, double x0 = 0)
double	chisquared_pdf(double x, double r, double x0 = 0)
double	exponential_pdf(double x, double lambda, double x0 = 0)
double	fdistribution_pdf(double x, double n, double m, double x0 = 0)
double	gamma_pdf(double x, double alpha, double theta, double x0 = 0)
double	gaussian_pdf(double x, double sigma = 1, double x0 = 0)
double	landau_pdf(double x, double s = 1, double x0 = 0.)
double	lognormal_pdf(double x, double m, double s, double x0 = 0)
double	normal_pdf(double x, double sigma = 1, double x0 = 0)
double	poisson_pdf(unsigned int n, double mu)
double	tdistribution_pdf(double x, double r, double x0 = 0)
double	uniform_pdf(double x, double a, double b, double x0 = 0)

Sampling from Prob Dist in ROOT

You can also use ROOT to generate random numbers according to a given probability distribution.

In the example generates 1000 random numbers from a Poisson Parent population with a mean of 10

root [0] TRandom r                                     
root [1] TH1F *P10=new TH1F("P10","P10",100,0,100)     
root [2] for(i=0;i<10000;i++) P10->Fill(r.Poisson(30));
Warning: Automatic variable i is allocated (tmpfile):1:
root [3] P10->Draw();                                  

Other possibilities

Gaussian with a mean of 30 and sigma of 5
root [1] TH1F *G10=new TH1F("G10","G10",100,0,100)     
root [2] for(i=0;i<10000;i++) G10->Fill(r.Gauss(30,5));  //mean of 30 and sigma of 5
root [3] G10->Draw("same");

There is also

G10->Fill(r.Uniform(20,50)); // Generates a uniform distribution between 20 and 50

G10->Fill(r.Exp(30)); // exponential distribution with a mean of 30

G10->Fill(r.Landau(30,5)); // Landau distribution with a mean of 30 and sigma of 5

G10->Fill(r.BreitWigner(30,5)); mean of 30 and gamma of 5

Forest_Error_Analysis_for_the_Physical_Sciences