TF SPIM StoppingPower

Stopping Power

Bethe Equation

Classical Energy Loss

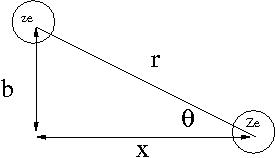
Consider the energy lost when a particle of charge ([math]ze[/math]) traveling at speed [math]v[/math] is scattered by a target of charge ([math]Ze[/math]). Assume only the coulomb force causes the particle to scatter from the target as shown below.

Notice

as [math]ze[/math] is scattered the horizontal component of the coulomb force ([math]F[/math]) flips direction; ie net horizontal force for the scattering

[math]F_{vertical} = k \frac{zZe^2}{r^2} \sin(\theta) = k \frac{zZe^2}{r^2} \frac{b}{r}[/math]

where

k =[math]\frac{1}{4 \pi \epsilon_0}[/math]

r = distance between incident projectile and target atom

b= impact parameter of collision

Using the definition of Impulse one can determine the momentum change of [math]ze[/math] as

[math]\Delta p = \int F dt[/math]

Let's assume that the energy lost by the incident particle [math]ze[/math] is absorbed by an electron in the target atom. This energy may be cast in terms of the incident particles momentum change as

[math]\frac{(\Delta p)^2}{2m_e}[/math]

By calculating the change in momentum ([math]\Delta p[/math]) of the incident particle we can infer that the energy lost by the incident particle is absorbed by one of the target material's atomic electrons.

[math]\Delta P = \int F dt = \int k \frac{zZe^2b}{r^3} dt[/math]

using [math]dt = \frac{dx}{v} = \frac{d x}{\beta c}[/math] we have

[math]= k \frac{zZe^2b}{\beta c} \int_{-\infty}^{+\infty} \frac{ dx}{(x^2+b^2)^{3/2}}[/math]

[math]=\frac{kzZe^2b}{\beta c b^2} \int_{-\infty}^{+\infty} \frac{ dx/b}{(1+\frac{x^2}{b^2})^{3/2}}[/math]

[math]\int_{-\infty}^{+\infty} \frac{ dx/b}{(1+\frac{x}{b^2})^{3/2}}=2[/math]

[math] \Delta p = \frac{2kzZe^2b}{\beta c b^2}[/math]

casting this in terms of the classical atomic electron radius [math]r_e[/math]

[math]r_e = \frac{k e^2}{m_e v^2} \sim \frac{k e^2}{m_e c^2}[/math] just equate [math]F = \frac{ke^2}{r_e^2} = m \frac{v^2}{r_e}[/math]

Then

[math] \Delta p = \frac{2zZr_e m_e c}{\beta b}[/math]

and

[math]\Delta E = \frac{(\Delta p)^2}{2m_e} = 2 \left ( \frac{r_e m_e}{\beta b}\right )^2 \frac {z^2 Z^2 c^2}{m_e}[/math] : [math]Z[/math] = 1 here because I shall assume the energy is lost to just the electron and the Atom is a spectator

Now let's calculate an expression representing the AVERAGE energy lost for an incident particle traversing a material of some thickness.

Let

[math]P(\Delta E)[/math] = Probability of an interaction taking place which results in an energy loss [math]\Delta E[/math]

If we let

Z = Atomic Number = # electrons in target Atom = number of protons in an Atom

N = Avagadros number = [math]6.022 \times 10^{23} \frac{Atoms}{mol}[/math]

A = Atomic mass = [math]\frac{g}{mole}[/math]

[math]dP(\Delta E)[/math] = probability of hitting an atomic electron in the area of an annulus of radius ([math]b + db[/math]) with an energy transfer between [math]\Delta E[/math] and [math]\Delta E + d(\Delta E)[/math]

Then

[math]\frac{-dE }{dx}= \int_0^{\infty} dP(\Delta E) \Delta E[/math] = energy lost by the incident particle per distance traversed through the material

I am just adding up all the energy losses weighted by the probability of the energy loss to find the total energy loss.

What is [math]dP(\Delta E)[/math]

[math]dP(\Delta E)[/math] = probability of an energy transfer taking place = probability of an interaction = [math]\frac{N}{A} d \sigma[/math] [ Atoms [math]m^2[/math]/g]

[math]dP(\Delta E) = \frac{N}{A} d \sigma =\frac{N}{A} (2 \pi b db) Z[/math]

classically [math]\sigma = \pi b^2 ; d \sigma = 2\pi b db[/math]

In practice [math] \sigma[/math] is a measured cross-section which is a function of energy.

[math]\Rightarrow \frac{-dE}{dx} = \int_0^{\infty} \frac{N}{A} (2 \pi b db) Z \Delta E = \frac{2 \pi N Z}{A} \int_0^{\infty} \Delta E b db[/math]

= [math]\frac{2 \pi N Z}{A} \int_0^{\infty} \left [ \frac{2 r_e^2 m_e c^2 z^2}{\beta^2 b^2}\right ] b db[/math]

= [math]4 \pi N r_e^2 m_e c^2 \frac{z^2 Z}{A \beta^2} \int_0^{\infty} \frac{db}{b}[/math]

=[math]\frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \int_0^{\infty} \frac{db}{b}[/math]

where [math]\frac{\mathcal{K}}{A} = \frac{4 \pi N r_e^2 m_e c^2}{A} = 0.307 \frac{MeV cm^2}{g}[/math] if A=1

The limits of the above integral should be more physical in order to reflect the limits of the physics interaction. Let b_{min} and b_{max} represent the minimum and maximum possible impact parameter where the physics is discribed, as shown above, by the coulomb force.

What is [math]b_{min}[/math]?

if [math]b \rightarrow 0[/math] then [math]\frac{d E}{dx}[/math] diverges and the energy transfer [math]\rightarrow \infty : \Delta E \sim \frac{1}{b}[/math]. Physically there is a maximum energy that may be transferred before the physics of the problem changes (ie: nuclear excitation, jet production, ...). The de Borglie wavelength of the atom is used to estimate a value for [math]b_{min}[/math] such that

[math]b_{min} \sim \frac{1}{2} \lambda_{de Broglie} = \frac{h}{2p} = \frac{h}{2 \gamma m_e \beta c}[/math]

What is [math]b_{max}[/math]?

As [math]b[/math] gets bigger the interaction is "softer" and longer. If the interaction time ([math]\tau_i[/math]) is so long that it is equivalent to an electron orbit ([math]\tau_R[/math]) then the atom looks more like it is neutrally charged. You move from an interaction in which the electron orbit is perturbed adiabatically such that there is no orbit change and the minimum amount of energy is transferred to no interaction taking place because the atom is neutral.

Let

[math]\tau_i = \frac{b_{max}}{v} (\sqrt{1-\beta^2})[/math] : fields at high velocities get Lorentz contracted

[math]\tau_R \equiv \frac{h}{I}[/math] : I [math]\equiv[/math] mean excitation energy of target material ( [math]E = h \nu = h/ \tau[/math])

Condition for [math]b_{max}[/math] :

[math]\tau_i = \tau_R[/math]

[math]\Rightarrow b_{max} = \frac{h \gamma \beta c}{I}[/math]

[math]-\frac{dE}{dx} = \frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \int_0^{\infty} \frac{db}{b}[/math]

[math]= \frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \ln \frac{b_{max}}{b_{min}}[/math]

[math]= \frac{\mathcal{K} }{A} \frac{z^2 Z}{\beta^2} \ln \frac{2 \gamma^2 m_e \beta^2 c^2}{I}[/math]

Example 5: Find [math]\frac{dE}{dx}[/math] for a 10 MeV proton hitting a liquid hydrogen ([math]LH_2[/math]) target

A = Z=z=1
[math]m_e c^2[/math] = 0.511 MeV
I = 21.8 eV : see gray data point for Liquid [math]H_2[/math] From Figure 27.5 on pg 6 of PDG below.

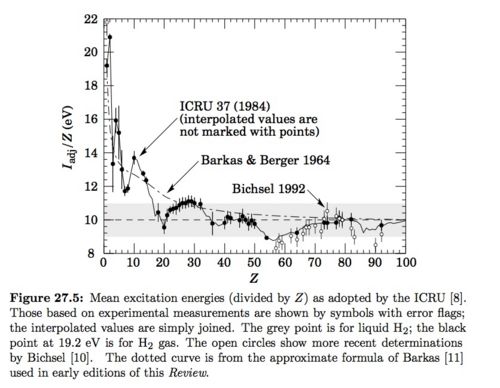
Just need to know [math]\gamma[/math] and [math]\beta[/math]

"a 10 MeV proton" [math]\Rightarrow[/math] Kinetic Energy (K.E.) = 10 MeV = [math](\gamma - 1) mc^2[/math]

[math]\Rightarrow \gamma = \frac{K.E.}{mc^2} + 1 = \frac{10 MeV}{938 MeV} + 1 \sim 1 = \frac{1}{\sqrt{1-\beta^2}}[/math]

Proton is not relativistic

[math]v^2 = \frac{2 K.E.}{m} = \frac{2 \cdot 10 MeV}{938 MeV/c^2} = 2 \times 10^{-2} c^2 \Rightarrow \beta^2 = \frac{v^2}{c^2} = 2\times 10^{-2}[/math]

Plugging in the numbers:

[math]\frac{dE}{dx} = \left ( 0.307 \frac{MeV \cdot cm^2}{g}\right ) (1)^2 (1) \frac{1}{2 \times10^{-2}} \ln \left( \frac{2 (1) (0.511 MeV) (2 \times10^{-2})}{21.8 eV} \frac{10^6 eV}{MeV}\right)[/math]

[math]= 105 \frac{MeV cm^2}{g}[/math]

How much energy is lost after 0.3 cm?

Notice that the units for energy loss are normalized by the density of the material [math]\rho_{LH_2}[/math] = 0.07 [math]\frac{g}{cm^3}[/math]

To get the actual energy lost I need to multiply by the density. So for any given atom the energy loss will depend on the state (solid, gas, liqid) of the atom as this effects the density of the material.

[math]\Delta E = (105 \frac{MeV cm^2}{g}) (0.07 \frac{g}{cm^3}) (0.3 cm)[/math] = 2.2 MeV

File:SPIM HydrogenStoppingPower.pdf Compare with Triumf Kinematics Handbook, 2nd edition, September 1987, L.G. Greeniaus

Bethe-Bloch Equation

While the classical equation above works in a limited kinematic regime, the Bethe-Bloch equation includes the corrections needed to cover most kinematic regimes for heavy particle energy loss.

[math]-\frac{dE}{dx} = \mathcal{K} z^2 \frac{Z}{A} \frac{1}{\beta^2} \left [ \frac{1}{2} \ln \left (\frac{2 m_2 c^2 \beta^2 \gamma^2 T_{max}}{I^2} \right) - \beta^2 - \frac{\delta}{2}\right ][/math]PDG reference Eq 27.1 pg 1

where

[math]T_{max} = \frac{2 m_e c^2 \beta^2 \gamma^2}{1+ \frac{2 \gamma m_e}{M} + \frac{m_e}{M}}[/math]

= Max K.E. transferable to the Target of mass [math]M[/math] in a single collision.

[math]-\beta^2[/math]

= correction for electron spin and very distant collisions which deforms the electron atomic orbits each process reducing dE/dx by [math]\frac{\beta}{2}[/math]

[math]\frac{\delta}{2}[/math]

= density correction term: in the classical derivation the material is treated as just a system of [math]N[/math] atoms uniformly distributed in space. These Atoms, however, give the material polarizability which can reduce the electric field (dielectric).

GEANT 4 implementation

The GEANT4 file (version 4.8.p01)

source/processes/electromagnetic/standard/src/G4BetheBlockModel.cc

is used to calculate hadron energy loss.

line 132 [math]\Rightarrow[/math]

[math]-\frac{dE}{dx} = \log \left ( \frac{2 m_e c^2 \tau (\tau +2) E_{min}}{I^2}\right) - \left (1 - \frac{E_{min}}{E_{max}} \right ) \beta^2[/math]

where

[math] \tau = \frac{K.E.}{M}[/math]

line 143 [math]\Rightarrow[/math]

[math]\frac{dE}{dx} -= \log ( \tau (\tau + 2) ) -cden[/math] = density corection = [math]\frac{\delta}{2}[/math]

line 148 [math]\Rightarrow[/math]

[math]\frac{dE}{dx} -= \frac{2c}{Z_{target}}[/math] = shell correction, corrects for the classical asumption that the atomic electron's velocity is initially zero; or the the incident particles velocity is far greater than the atomic electron's velocity.

line 154 [math]\Rightarrow[/math]

[math]\frac{dE}{dx} *= \frac{2 \pi m_e c^2 r_e^2 z^2}{\beta^2} \rho_e \;\;\;\; \rho_e \propto \frac{NZ}{A}[/math]

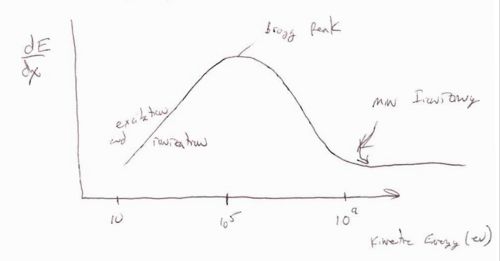
Energy Dependence

The above curve shows the energy loss per distance traveled ([math]\frac{dE}{dx}[/math]) as a function of the incident particles energy. There are three basic regions. At low incident energies ( < 10^5 eV) the incident particle tends to excite or even ionize the atoms in the material it is penetrating. The maximum amount of energy loss per distance traveled is defined at as the Bragg peak. The region after the Bragg peak in which the energy loss per distance traveled reaches its smallest value is refered to as the point of minimum ionizing. Minimimum ionizing particles will have incident energies corresponding to this value or larger. The characteristic of the minimum ionizing particles is that their energy loss per distance traveled is essentially constant making simulations easier until the particle's energy drops below the minimum ionizing energy level as it passes through the material.

In general the Bethe-Bloch equation breaks down at low energies (below the Bragg peak) and is a good description (to within 10%) for

[math]10 \frac{MeV}{a.m.u.} \lt E \lt 2 \frac{GeV}{a.m.u.}[/math] and [math]Z[/math] < 26 (Iron) : a.m.u = Atomic Mass Unit

the [math]\frac{1}{\beta^2}[/math] term in the Bethe-Bloch equation dominates between the Bragg peak and the minimum ionization region.

the [math]\ln[/math] term and its corrections influence the dependence of [math]\frac{dE}{dx}[/math] as you move up in energy beyond the minimum ionization point.