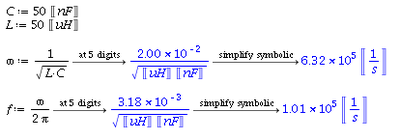Go Back to All Lab Reports
- LC Resonance circuits
The LC cicuit
 ==Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use [math]L[/math] = 10 - 100 [math]\mu H[/math], R = 1k
[math]\Omega[/math]==
==Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use [math]L[/math] = 10 - 100 [math]\mu H[/math], R = 1k
[math]\Omega[/math]==
- [math]\omega_0=\frac{1}{\sqrt{\mbox{LC}}}[/math]
I choose the following values for [math]\mbox{R}[/math] and [math]\mbox{C}[/math]:
- [math]R=aaa\ \Omega[/math]
- [math]C=bbb\ \mu F[/math]
So the resonance frequency is [math]\omega_0=\frac{1}{\sqrt{aaa\ \Omega\ bbb\ \mu F }} = ccc\ \frac{\mbox{rad}}{\mbox{sec}}[/math]
Or [math]f=\frac{\omega_0}{2\pi} = ddd\ \mbox{kHz}[/math]
Let's estimate:
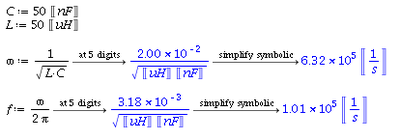
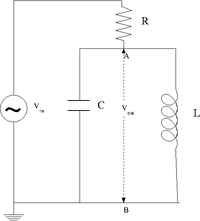
Construct the LC circuit using a non-polar capacitor
Measure the Gain [math]\equiv \frac{V_{out}}{V_{in}}[/math] as a function of frequency. (25 pnts)
#Compare the measured and theoretical values of the resonance frequency ([math]\omega_{L}[/math]) (10 pnts)
Questions
Is there a value of [math]R[/math] in which [math]V_{out} \approx V_{in}[/math] at resonance. What is the value?(5 pnts)
The RLC cicuit
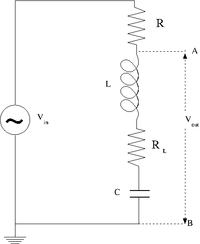
Design and construct a series LRC circuit
Measure and Graph the Gain as a function of the oscillating input voltage frequency. (25 pnts)
Measure and Graph the Phase Shift as a function of the oscillating input voltage frequency. (25 pnts)
Questions
What is the current [math]I[/math] at resonance? (5 pnts)
What is the current as [math]\nu \rightarrow \infty[/math]? (5 pnts)
Forest_Electronic_Instrumentation_and_Measurement
Go Back to All Lab Reports
 ==Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 , R = 1k
==
==Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 , R = 1k
==