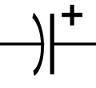TF EIM Chapt2

Alternating Current (AC)

Thus far we have discussed direct current circuits which were built from a battery (constant voltage supply).

Another type of circuit is one in which the current is driven in an alternating fashion. Typically the current is increased so some positive maximum value, then decreased until it passes through zero and reverses direction until it reaches another maximum value and then it is decreased again, passing though zero once more on its way to a positive maximum value.

Definitions

frequency ([math]f[/math], [math]\nu[/math] )

The frequency is number of complete cycles which occur in 1 sec (cycles/sec = Hz)

Angular frequency =[math] \omega = 2\pi f[/math] = radians/sec

Period

The period is the time to complete one cycle = 1/[math]f[/math]

Amplitude

The change in the current from zero to its most positive value

peak-to-peak

The amount the current changes from its largest positive value to its most negative.

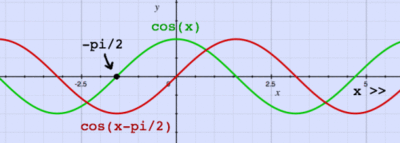
phase

The time a current takes to reaches its maximum value compared to another alternating current

Note

The above definitions can be used for voltage as easily as current.

Mathematical description

Trigonometric

[math]I(t) = \sin(\omega t + \phi) = \cos(\omega t + \phi - \pi/2)[/math]

Note

A 180 degree ([math]\pi[/math] radian) phase shift will put the above cosine wave completely out of sync with the original one such that if we add the two signals together the net current would be zero.

I_{RMS}

With this functional form for the alternating current we can now calculate another property, the RMS or root mean square.

The RMS quantifies an average fluctuation of the alternating current such that

[math]I_{RMS} \equiv \sqrt{\frac{1}{T} \int_0^T I^2(t) dt} = \sqrt{\frac{1}{T} \int_0^T I_0^2 \sin^2(\omega t) dt}= \frac{I_0}{\sqrt{2}} [/math]

where T represent the time interval over which the average is calculated ([math]\infty[/math])

[math]\int_0^T \sin^2(x) dx = \int_0^T \frac{1}{2} \left (1 - \cos(2x) \right) dx = \frac{1}{2} + \frac{1}{T} \int_0^T \cos(t)dt = \frac{1}{2}[/math] if T is infinite or an integer number of cycles

Power

The instantaneous power dissipated in a resister by an alternating current is given as

[math]P_{inst}(t) =I^2(t) R = R\sin^2(\omega t)[/math]

Average power

[math]P_{ave} = \frac{1}{T} \int_0^T P(t) dt = \frac{1}{T} \int_0^T RI^2(t) dt = \frac{R}{T} \int_0^T \sin^2(\omega t) dt = \frac{I_0^2R}{\sqrt{2}} = I_{RMS}^2 R[/math]

Plane waves

Another mathematical expression for an alternating current uses complex variables

[math]I\left ( \omega t \right )=I_0 \exp^{i \left ( \omega t \right )} = I_0 \left ( \cos \left ( \omega t \right) + i \sin \left ( \omega t \right) \right )[/math]

Expressing the current in this form will be useful later

Voltage sources of AC current

The circuit symbol for an emf used to drive alternating currents is given below

The mathematical form is

[math]V = V_0 \sin(\omega t)[/math]

Capacitors

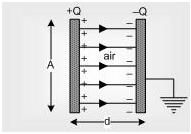
A capacitor is a device used to store charge in a circuit. The simplest capacitor is built from two conducting plates placed close to each other.

Noteice

The potential is constant over the face of the capacitor

[math]V_{AB} = - \int_A^B \vec{E} \cdot d \vec{l}[/math]

The symbol for a capacitor in a circuit reflects this.

dielectric

dielectric capacitors can be shorted out. Put the positive probe from the voltmeter on the positive side of the electrolytic capacitor, the capacitor should be good if you measure a large resistance [math](k \Omega)[/math] otherwise a shorted electrolytic capacitor (small resistance) is a bad one.

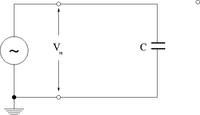
Capacitor circuit

If

[math]V=V_0 cos(\omega t)[/math]

then applying loop theorem lead to

[math]V-\frac{Q}{C} = 0[/math]

[math]Q = VC= V_0 C \cos{\omega t)}[/math]

[math]I = \frac{dQ}{dt} = -V_0C \omega \sin(\omega t)= V_0 C \omega \cos(\omega t + \pi/2)[/math]

Notice that the current is 90 degrees out of phase with the driving voltage.

Note

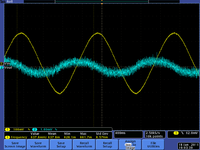
The current increases faster than the voltage. Below are a few scope pictures measuring the voltage coming out of the voltage source [math](V_{in})[/math] and the voltage on the ground side of the capacitor [math](V_{out})[/math] (the capacitor is grounded through the scope).

1 Hz	10kHz	MHz
Capacitor response at low frequency	File:TF EIM CapChargeScopePic kHz.png kHz frequency	File:TF EIM CapChargeScopePic MHz.png MHz frequency

Resistive nature of capacitance

To illustrate the resistive nature of capacitors, let's write the driving voltage in using complex notation

[math]V=V_0 \cos(\omega t) = V_0 Re \left [ e^{i\omega t} \right ][/math]

The notation

[math] e^{\omega t} = \cos(\omega t) + i \sin(\omega t)[/math]: Euler's equation

[math] Re \left [ e^{i\omega t} \right ]=Re \left [ \cos(\omega t) + i \sin(\omega t) \right ]= \cos(\omega t) [/math] The real part of a complex variable.

The current is written as

[math]I=\omega CV_0 Re \left [ e^{i \left (\omega t + \phi \right ) } \right ][/math]

[math] \omega C V_0 Re \left [ e^{i \left ( \omega t + \phi \right )} \right ][/math]

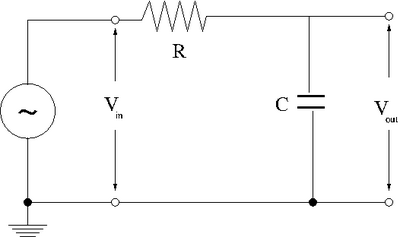
RC circuit

Now add a resistor in series with the capacitor in the above capacitor charging circuit.

Again apply the loop theorem

[math]V -IR -\frac{Q}{C} =0[/math]

or

[math]R \frac{dQ}{dt} + \frac{1}{C} Q - V = 0[/math] First order linear differential equation

Forest_Electronic_Instrumentation_and_Measurement