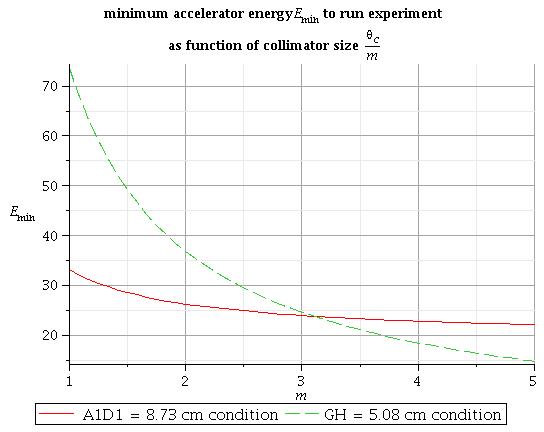
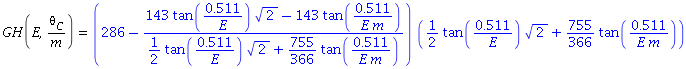Minimum accelerator energy to run experiment

Go Back

general setup

fitting the collimator size into the hole through the concrete wall

I can express the distance [math]A_1D_1[/math] as function of collimator size [math]\Theta_C/m[/math] and electron beam energy E:

[math]A_1D_1(E,\ \Theta_C/m) = \frac{469}{\sqrt{2}}\tan\left(\frac{0.511}{E}\right)
                              + \frac{469}{2}\tan\left(\frac{1}{m}\frac{0.511}{E}\right)[/math]

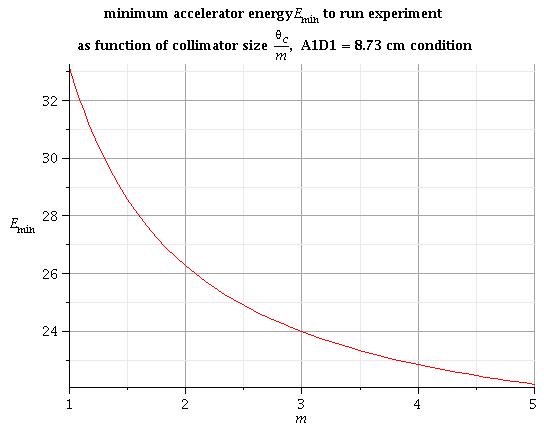
To fit the collimator size into the hole through the concrete wall with radius R = 8.73 cm we need to solve equation:

[math]A_1D_1(E,\ \Theta_C/m) = 8.73\ cm[/math]

1) some solutions of this equation for different collimator sizes m are:

[math]m = 1 \Rightarrow E_{min} = 33.1\ MeV  [/math]

[math]m = 2 \Rightarrow E_{min} = 26.3\ MeV  [/math]

[math]m = 4 \Rightarrow E_{min} = 22.8\ MeV  [/math]

2) in general for arbitrary collimator size m the solutions are:

All energies under this line is good to run experiment for condition above

critical collimator line condition

Also I can express the distance [math]GH[/math] as function of collimator size [math]\Theta_C/m[/math] and electron beam energy E:

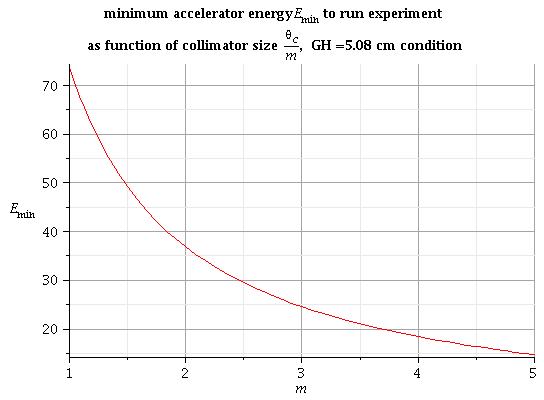
If I would like that nothing hitting the 4" box to go through the collimator I need to solve equation:

[math]GH(E,\ \Theta_C/m) = 5.08\ cm[/math]

1) some solutions of this equation for different collimator sizes m are:

[math]m = 1 \Rightarrow E_{min} = 73.7\ MeV  [/math]

[math]m = 2 \Rightarrow E_{min} = 36.9\ MeV  [/math]

[math]m = 4 \Rightarrow E_{min} = 18.4\ MeV  [/math]

2) in general for arbitrary collimator size m the solutions are:

All energies under this line is good to run experiment for condition above

both solutions together

All energies under this lines is good to run experiment for both conditions above

Go Back